线段树-SegmentTree（简洁版）

这篇简单说下线段树线段树（Segment Tree），顾名思义它是用来存放给定区间（segment, or interval）内对应信息的一种数据结构。与树状数组（Binary Indexed Tree）相似，线段树也用来处理数组相应的区间查询（range query）和元素更新（update）操作。与树状数组不同的是，线段树不止可以适用于区间求和的查询，也可以进行区间最大值，区间最小值（Range Minimum/Maximum Query problem）或者区间异或值的查询。

对应于树状数组，线段树进行更新（update）的操作为O(logn)，进行区间查询（range query）的操作也为O(logn)。

下面以LeetCode 307. Range Sum Query – Mutable为例来讲解：

307题目大意是：给你一个数组，再给你一个范围，让你求这个范围内所有元素的和，其中元素的值是可变的，通过update(index, val)更新。 

nums = [1, 3, 5]，
sumRange(0, 2) = 1+3+5 = 9
update(1, 2) => [1, 2, 5]
sumRange(0, 2) = 1 + 2 + 5 = 7

01.暴力求解就是扫描一下这个范围。

时间复杂度：Update O(1), Query O(n)。

02.如果数组元素不变的话（303题），我们可以使用动态规划求出前n个元素的和然后存在前缀和数组sums中。i到j所有元素的和等于0~j所有元素的和减去0~(i-1)所有元素的和，即：

if i > 0     sumRange(i, j) = sums[j] – sums[i – 1]

else        sumRange(i, j) =sums[j]

这样就可以把query的时间复杂度降低到O(1)。

但是这道题元素的值可变，那么就需要维护sums，虽然可以把query的时间复杂度降低到了O(1)，但update的时间复杂度是O(n)，并没有比暴力求解快。

03.这个时候就要请出我们今天的主人公Segment Tree了，可以做到 ： Update: O(logn)，Query: O(logn+k)

其实Segment Tree的思想还是很好理解的，比我们之前讲过的Binary Indexed Tree要容易理解的多，但是代码量又是另外一回事情了…

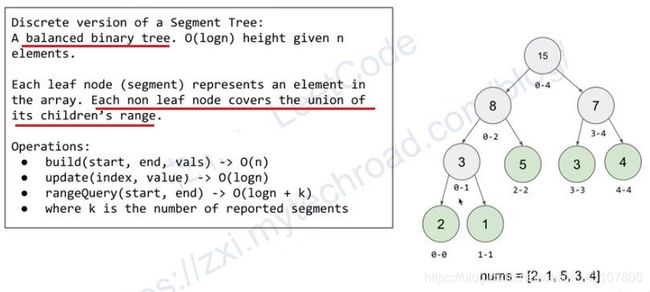
感觉前面都是废话，进入正题吧，首先从数据结构的角度来说，线段树是用一个完全二叉树来存储对应于其每一个区间（segment）的数据。该二叉树的每一个结点中保存着相对应于这一个区间的信息。同时，线段树所使用的这个二叉树是用一个数组保存的，与堆（Heap）的实现方式相同。当然了，完全可以将每个node封装到结构体中，父节点有指向子节点的指针，然后组成一颗真正意义上的完全二叉树。具体视情况而定吧。

下图中的线段树，每个叶子节点代表数组中的元素，每个非叶节点覆盖它的子节点，

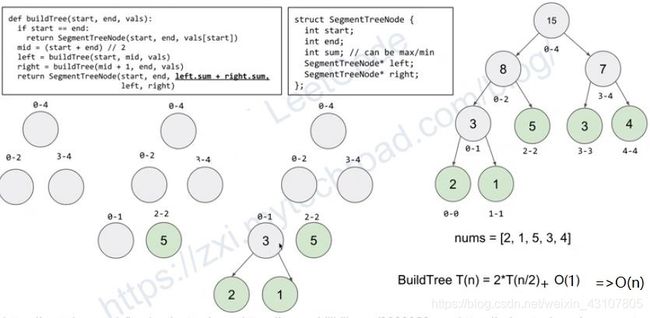
建树：分而治之的思想，每个master负责他的两个子节点的建设，以及自己要整合两个子节点的结果，递归+分治

 

查询：递归+分治，     

LeetCode 307. RangeSum Query – Mutable

//running time: 24 ms
class SegmentTreeNode {
public:
  SegmentTreeNode(int start, int end, int sum,
                  SegmentTreeNode* left = nullptr,
                  SegmentTreeNode* right = nullptr): 
    start(start),
    end(end),
    sum(sum),
    left(left),
    right(right){}      
  SegmentTreeNode(const SegmentTreeNode&) = delete;
  SegmentTreeNode& operator=(const SegmentTreeNode&) = delete;
  ~SegmentTreeNode() {
    delete left;
    delete right;
    left = right = nullptr;
  }
  
  int start;
  int end;
  int sum;
  SegmentTreeNode* left;
  SegmentTreeNode* right;
};
 
class NumArray {
public:
  NumArray(vector nums) {
    nums_.swap(nums);
    if (!nums_.empty())
      root_.reset(buildTree(0, nums_.size() - 1));
  }
 
  void update(int i, int val) {
    updateTree(root_.get(), i, val);
  }
 
  int sumRange(int i, int j) {
    return sumRange(root_.get(), i, j);
  }

private:
  vector nums_;
  std::unique_ptr root_;
  
  SegmentTreeNode* buildTree(int start, int end) {  
    if (start == end) {      
      return new SegmentTreeNode(start, end, nums_[start]);
    }
    int mid = start + (end - start) / 2;
    auto left = buildTree(start, mid);
    auto right = buildTree(mid + 1, end);
    auto node = new SegmentTreeNode(start, end, left->sum + right->sum, left, right);    
    return node;
  }
  
  void updateTree(SegmentTreeNode* root, int i, int val) {
    if (root->start == i && root->end == i) {
      root->sum = val;
      return;
    }
    int mid = root->start + (root->end - root->start) / 2;
    if (i <= mid) {
      updateTree(root->left, i, val);
    } else {      
      updateTree(root->right, i, val);
    }
    root->sum = root->left->sum + root->right->sum;
  }
  
  int sumRange(SegmentTreeNode* root, int i, int j) {    
    if (i == root->start && j == root->end) {
      return root->sum;
    }
    int mid = root->start + (root->end - root->start) / 2;
    if (j <= mid) {
      return sumRange(root->left, i, j);
    } else if (i > mid) {
      return sumRange(root->right, i, j);
    } else {
      return sumRange(root->left, i, mid) + sumRange(root->right, mid + 1, j);
    }
  }

};

segmentTree如果想要更节约时间的话，还有lazy操作，可以看我之前的文章：https://blog.csdn.net/weixin_43107805/article/details/89430826