字典树（trie）——杨子曰数据结构

字典树（trie）——杨子曰数据结构

先扔一道题：HDU - 1251统计难题
就是说给你一堆字符串，再是一堆询问，问你以这个字符串为前缀的字符串有多少个？

---

今天我们来曰一个字符串中常用的数据结构——字典树（高雅的人称之为trie树（读作：踹树））
trie树有一下几个特点：
1.根节点是空的
2.每个节点上都会记录一个字符（除了根节点）
3.从根节点下面出发，往下走路径上记录字符串，So，两个串相同的前缀是它们后缀的公共祖先
我都觉得我没有讲清楚，相信你也一脸懵逼，于是我们来搞一个例子：
假设我们要把一下字符串放进trie：

aab
ab
abbc
abba
ac
bbb
bbc
ba
bac
cca

我们可以得到这样一棵trie树：
蓝色的节点表示这个节点是一个字符串的结尾，也就是从根到蓝色节点的路径上是是一个串

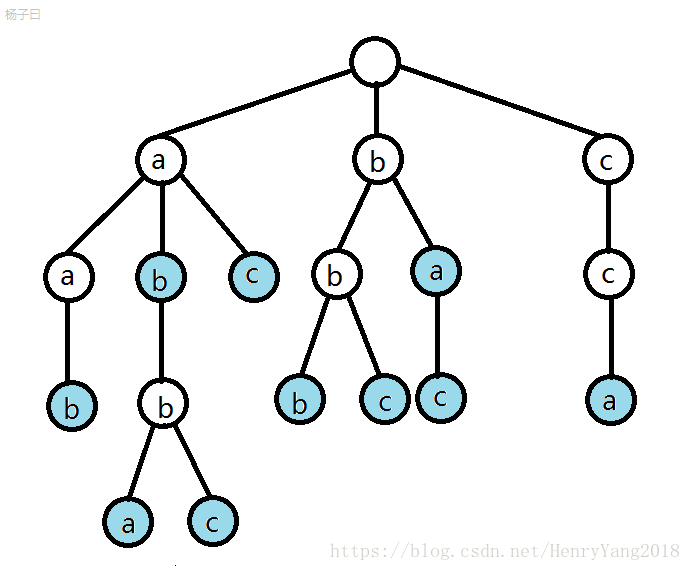
只要你是地球人就能秒懂
那我们怎么建树呢？，可以说是非常滴简单呀！！直接上代码：

                                      //tr[k][p]表示节点k的字符为p的儿子的编号
void build(string s){                 //我们要把s放进trie里
	int k=1;                          //根节点是1，我们现在在k节点
	for (int i=0;s[i];i++){
		int p=s[i]-'a';
		if (!tr[k][p]) tr[k][p]=++sum;//如果这个节点不存在，那就建一个,并把当前节点的这条边指向它
		k=tr[k][p];                   //继续往下走
	}
}

很显然trie能解决的问题都和前缀有很大关系，解决问题时我们要考虑在trie上是否要记录东西？记录什么东西？
这些东西可以是：这个节点是不是一个串的结尾，这个节点经过了几次……（我也一时半会儿举不出，尴尬）
到现在为止，我们会发现上面那个问题会变得灰常简单了，我们要在每个节点记录它在建树是时经过的次数，也就是所有字符串中，以根节点到这个节点路径上的字符串为前缀的字符串个数（←，很绕，自己模拟一下）
Then，对于每次查询我们从根出发，找到这个字符串末尾的节点，输出节点上记录的值就欧了。
代码走起：

int find(char *s){
	int k=1;
	for (int i=0;s[i];i++){
		int p=s[i]-'a';
		if (!tr[k][p]) return 0;//这个前缀不存在
		k=tr[k][p];
	}
	return num[k];
}

总结一波：建树复杂度O（n|s|），查询复杂度O（|s|），可以说是非常优啊！
OK，完事

---

c++代码：

#include
#include
using namespace std;

char s[100];
int sum=1;
int tr[500005][30],num[500005];

void build(char *s){
	int k=1;
	for (int i=0;s[i];i++){
		int p=s[i]-'a';
		if (!tr[k][p]) tr[k][p]=++sum;
		k=tr[k][p];
		num[k]++;
	}
}

int find(char *s){
	int k=1;
	for (int i=0;s[i];i++){
		int p=s[i]-'a';
		if (!tr[k][p]) return 0;
		k=tr[k][p];
	}
	return num[k];
}

int main(){
	while(gets(s) && s[0]) build(s);
	while(~scanf("%s",&s)){
		cout<<find(s)<<endl;
	}
	return 0;
}

注意：
对于有些题目，你要考虑把哪些字符串放进trie，推荐一道题：POJ - 1204 Word Puzzles
你以为字典树只能解决字符串的问题吗？推荐一道题：[HDU 4825 - Xor Sum]
(https://blog.csdn.net/HenryYang2018/article/details/81452474)

---

如果你还知道一个东西叫KMP的话（不知道，戳）
字典树是妈妈，KMP是爸爸，会有一个小孩纸叫做AC自动机（注意！不是自动AC机，他们有本质区别）
戳我学习自动AC AC自动机
他是一个用KMP的想法在trie树上实现的算法

于XJ机房607