平衡树之Treap(树堆)——杨子曰数据结构
平衡树之Treap(树堆)——杨子曰数据结构
来道题(Tyvj 1728 / HYSBZ - 3224):
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入x数
- 删除x数(若有多个相同的数,因只删除一个)
- 查询x数的排名(若有多个相同的数,因输出最小的排名)
- 查询排名为x的数
- 求x的前驱(前驱定义为小于x,且最大的数)
- 求x的后继(后继定义为大于x,且最小的数)
Input
第一行为n,表示操作的个数,下面n行每行有两个数opt和x,opt表示操作的序号(1<=opt<=6)
Output
对于操作3,4,5,6每行输出一个数,表示对应答案
Sample Input
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
Sample Output
106465
84185
492737
Hint
- n的数据范围:n<=100000
- 每个数的数据范围:[-2e9,2e9]
没有什么废话好说了这是我写过的最正经的博客了,咱们直接进入正题:
如果你知道什么是二叉查找树和平衡树你可以跳过这一段(你也可以看看,这很有意思)
首先你要知道一种树,它叫二叉查找树,这棵树只有一个性质:某个结点左子树中的权值都小于它,右子树中的所有权值都大于它,于是乎,你会发现这个数据结构就是为这道题量身定做的有没有!对于新加进来的数字,从根节点开始,比当前节点大就往左走,比当前节点小就往右走。你只需要记录每颗子树的大小,然后再胡乱搞搞就好了(下面会具体讲)
我们都知道出数据的人,一个比一个变态,你被卡的越惨,它们就越高兴,于是它们就制造了一种数据叫做:不断插入升序的数,每次插入时,这个数都不停地往右走,于是你会发现二叉查找树变成了一条链!所有的操作都变成O(n)了!!!
So,机智的人类就发明了一种牛逼的数据结构——平衡树
这种树就专门就专门用来防止二叉查找树退化成链,防止二叉查找树退化成链有n多种方法,于是就诞生了各种各样的平衡树:红黑树、AVL、Treap、伸展树、SBT、替罪羊树
我们今天就曰一种:Treap
先来讲一讲这个英文单词是怎么造出来的:Treap=Tree+heap(?特别粗暴有没有)
机智的你一定发现了,它就是二叉查找树和堆的结合(So,如果你不会堆的话:戳)
它的核心思想就是给树上的每个节点都取一个随机值(rd[i]),在维护二叉查找树的同时去维护这个随机值成一个大根堆(你喜欢小根堆也行),只要是人品正常的人,最终出来的二叉查找树是比较平衡的
黑喂狗:
先来了解一下Treap上的每个节点都要保存那些信息:
- v[i]:节点i的权值,就是题目中所要操作的数
- num[i]:由于数字可能会重复,我们要把重复的数字存在同一个节点上,这就记录了给节点上有一个v[i]
- sz[i]:以节点i为根节点的子树中记录了多少给数字
- rd[i]:随机产生的一个数,把它们维护成大(小)根堆
- ch[i][0/1]:节点i的左/右儿子编号(可以通过异或运算找到它的兄弟)
首先我们要看的是,假设插入数或删除了一个数后,我们的大根对被破坏了肿么办?
这就涉及到一个操作——旋转(rotate)就是在保证了二叉查找树的同时维护了这个随机值的大根堆
比方说,这是树的一部分(节点上的数字是编号):

现在rd[1]
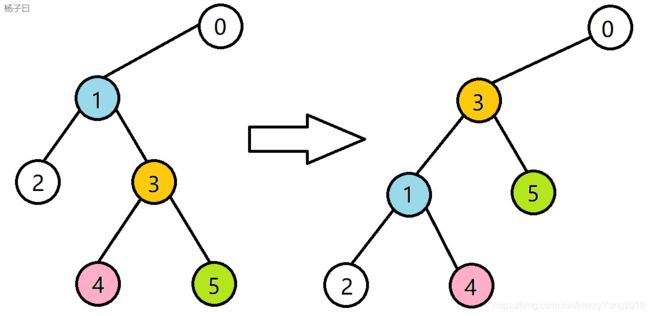
具体实现是这样滴:
把1的的右儿子赋成它的右儿子(也就是3)的左儿子,再把3的左儿子赋成1,最后再把0的左儿子赋成3
我们来讲一下为神马这样做可以同时维护二叉查找树和大根堆捏?
先来讲二叉查找树:
首先在插入或删除时,我们本身就是根据二叉查找树的性质来的(下面会详细讲怎么来)So,左图是维护好的二叉查找树,So,我们可以得到:v[3]>v[4]>v[1],因此1可以成为3的左儿子,4可以成为1的右儿子
再来曰大根堆:
由于在每次插入或删除结束后,要马上进行旋转操作,So,每次在堆中不和谐的只有可能是一个数而我们在插入或删除或删除时都是先做到叶子,再一点一点往上转的,So,当出现一组父子关系破坏了大根堆时,都是儿子惹的货,再上图中,只有3是不和谐的,因此我们可以得到rd[3]>rd[1]>rd[2],rd[4],rd[5],所以转成右图一点问题也没有
如果上面两段看不懂不要慌张,你只需要记住当rd[3]>rd[1]像图中那样转,同时维护了二叉查找树和大根堆
上图图中所示的是左旋,地球人都知道有一种东西叫右旋,就给张图吧(由于我太懒了,所以就把左右的树反转了一下,懂就行了,滑稽)
void rotate(int &o,int d){//d=0表示左旋,d=1表示右旋。下面的注释以左旋为例
int k=ch[o][d^1];//k是即将变成爸爸的儿子
ch[o][d^1]=ch[k][d];//把o的的右儿子赋成它的右儿子(也就是k)的左儿子
ch[k][d]=o;//再把k的左儿子赋成o
maintain(o);
maintain(k);//保证此时树上所记录的东西正确
o=k;//最后再把最顶上节点(就是我们图中所示的0)的左儿子赋成k
}
关于最后那个o=k我再多说几句:注意我函数的定义是传进了地址的,我在里面改了o,在外面我也会改掉我想改的东西(比如:图中所示的0的儿子),把这篇博客看完以后再回来看这个地方,你就理解了
maintain函数其实就是要维护一下sz的值:
void maintain(int o){
sz[o]=sz[ch[o][0]]+sz[ch[o][1]]+num[o];
}
旋转操作我们就结束了,准备工作完成!
接下来我们用二叉查找树逐一解决题目让我们做的操作:
- 插入x数(insert)
之前已经提到过了,我们从根节点出发,如果x小于当前节点的值,就走到左儿子,大于当前节点的值,就走到右儿子,有没有发现这其实就是一个二分,知道走到记录x的节点,或者一个空节点为止,当我们把x安放好后,要从下往上回溯,判断是否维护了大根堆,一单发现了不和谐现象,马上旋转
代码走起:
void insert(int &o,int val){
if (!o){
o=++sum;
sz[o]=num[o]=1;
v[o]=val;
rd[o]=rand();
return;
}
if (v[o]==val){
num[o]++;
sz[o]++;
return;
}
int d=(val>v[o]);
insert(ch[o][d],val);
if (rd[o]<rd[ch[o][d]]) rotate(o,d^1);
maintain(o);
}
- 删除x数(del)
如果我们想要删掉x,就得先在二叉查找树里找到x,我就不多说了吧(小就往左走,大就往右走),当我们找到这个x后:
如果这个节点上记录了多个x,那我们就把个数减1,美滋滋
如果这个节点上只有一个x:
①但是这个节点没有儿子,嗯,直接删掉,美滋滋
②如果这个节点有儿子,也就是说如果我把这个节点直接删掉的话,它的儿子就凌空了,肿么办捏?
这时候我们又要开始旋转了,我们可以把这个节点一直旋转到叶子节点,然后就可以开心地把它删掉了,但是注意旋转的时候需要维护rd的大根堆,So,如果转到的节点有两个儿子,就得把大的转上来,如果只有一个儿子,我就不多说了……
别忘了删完要maintain一下,这就有点像线段树的pushup
上代码:
void del(int &o,int val){
if (!o) return;
if (val<v[o]) del(ch[o][0],val);
else if (val>v[o]) del(ch[o][1],val);
else{
if (!ch[o][0] && !ch[o][1]){
num[o]--;sz[o]--;
if (num[o]==0) o=0;
}
else if (ch[o][0] && !ch[o][1]){
rotate(o,1);
del(ch[o][1],val);
}
else if (!ch[o][0] && ch[o][1]){
rotate(o,0);
del(ch[o][0],val);
}
else{
int d=(rd[ch[o][0]]>rd[ch[o][1]]);
rotate(o,d);
del(ch[o][d],val);
}
}
maintain(o);
}
- 查询x数的排名(rk)
还是那句话,我们要在树中找到x,找x的过程中如果往右走了,说明这个节点和这个节点的左子树中记录的所有数字都比x要小,我们就可以累加到当前的答案里,这完全就是一个二分,走到x的节点时答案+1就是最终排名,因为它要输出的是最小排名,Very easy
随手打出代码:
int rk(int o,int val){
if (!o) return 0;
if (v[o]==val) return sz[ch[o][0]]+1;
if (v[o]>val) return rk(ch[o][0],val);
if (v[o]<val) return sz[ch[o][0]]+num[o]+rk(ch[o][1],val);
}
- 查询排名为x的数(find)
这个操作和上面的rk几乎是一样的,你需要看的是当前节点左子树的sz,这样你就可以确定x在左子树还是在右子树中了,不过一定要注意:如果在右子树,记得把当前的排名减去左子树的sz
上代码:
int find(int o,int val){
if (!o) return 0;
if (sz[ch[o][0]]>=val) return find(ch[o][0],val);
else if (val>sz[ch[o][0]]+num[o]) return find(ch[o][1],val-(sz[ch[o][0]]+num[o]));
else return v[o];
}
- 求x的前驱
其实还是一个二分的实现过程,如果这个数小于等于当前节点,那么它的前驱也一定在左子树,否则,它的前驱有可能就是当前节点,或者在右子树,那我们就拿这两种情况取个max
走起:
int pre(int o,int val){
if (!o) return -inf;
if (v[o]>=val) return pre(ch[o][0],val);
else return max(v[o],pre(ch[o][1],val));
}
- 求x的后继
与上面完全相反(懒得说了(~﹃~)~zZ)
直接上代码:
int suc(int o,int val){
if (!o) return inf;
if (v[o]<=val) return suc(ch[o][1],val);
else return min(v[o],suc(ch[o][0],val));
}
至此,六个操作全部实现!
OK,完事
c++模板(Tyvj 1728 / HYSBZ - 3224):
#include于HG机房&TJQ高层小区