线段树（六）可持久化线段树 （主席树）——杨子曰算法

线段树（六）可持久化线段树 （主席树）——杨子曰算法

传送门：线段树集合

---

突然意识到一个问题，线段树应该是数据结构不应该说是杨子曰算法，算了算了……（逃

---

先来一道模板题：可持久化数组

---

这道题和以前的区别就在于他要查询历史的信息，也就是我们要把历史版本的信息也记录下来

“那我们对每一个历史版本都开一颗线段树”

这就是莽夫的行为，现在我们要解决的是内存和时间的问题

我们就需要用到可持久化线段树了

黑喂狗：

---

我们先来思考一下上面那个莽夫的行为：那我们对每一个历史版本都开一颗线段树

你会发现它非常浪费，而且没必要，原因如下：
这是一颗线段树（注意！可持久化线段树都是动态开点）

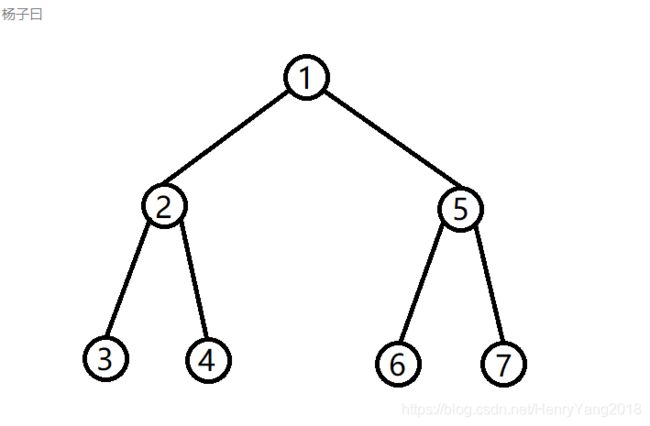
对于一颗线段树我们更改了一个节点上的信息，只有从它到根节点这条路径上的节点会被修改：

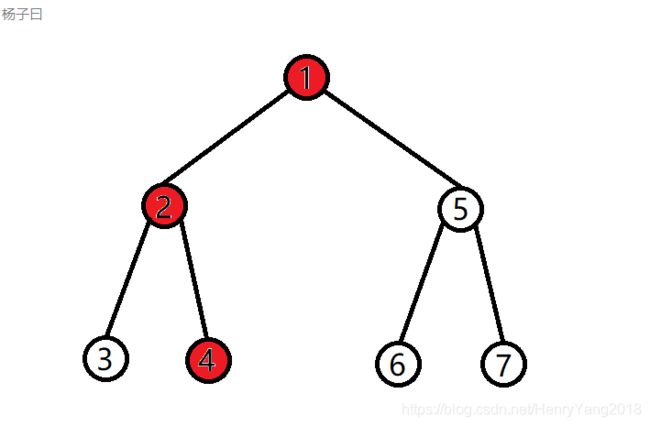
也就是相邻两个版本的线段树只有一条路径是不同的，而其他的都一样

那新的版本的线段树我们可不可以只建一条路径，其他的都沿用原来的？这就是可持久化线段树的中心思想了

比如我们要更改节点4，在保留原线段树的基础上建这样一条链：

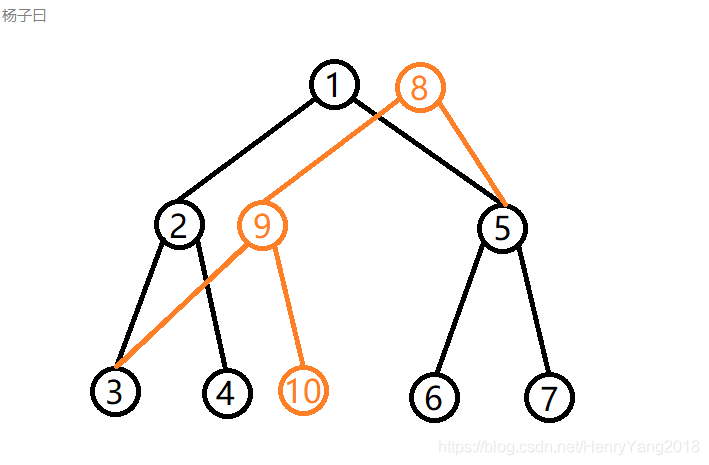
节点8，9，10就是在更改了节点4以后的节点1，2，4，（那么我们称节点1是节点8的前驱，节点2是节点9的前驱，节点4是节点10的前驱）比方说我们现在来看节点2，它的右儿子的信息改过了，So，节点9的右儿子就是10，但节点2的左儿子3没有发生任何变化，So，节点9的左儿子还是3，节点8也是一样的道理

这时，我们要记录版本2的根节点是8：rt[2]=8（rt[i]表示第i个版本的线段树的根节点，最开始rt[1]=1）

这样一来，对于每次更新我们都只需要多开log n个节点就可以了，So，空间和时间的复杂度：O(m log n)

---

我们来实现一下最上面的那到模板题由于它是单点查询某一个位置上的值，So，叶子节点上面的节点不许要记录任何信息，也就是我们不需要任何pushup
build就和原来完全一样（注意要动态开点，我觉得不会动态开点的童鞋也应该能看懂）：

void build(int l,int r,int &nod){
	nod=++tot;
	if (l==r){
		tr[nod].v=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(l,mid,tr[nod].ls);
	build(mid+1,r,tr[nod].rs);
}

接下来就是update，也就是我们可持久化线段树的核心了

首先，我们一路update下来的同时要建一个条新的链，So，update的时候我们所在的节点都是我们当前要新建的

我们在写update时候要把当前节点的前驱也传进去，还是看下面的注释比较清楚：

void update(int l,int r,int k,int val,int pre,int &nod){//nod表示我们当前走到的要新开的节点，pre是它的前驱
	nod=++tot;
	tr[nod]=tr[pre];//把它的前驱的信息暂时赋给当前这个节点
	if (l==r){
		tr[nod].v=val;//叶子节点
		return;
	}
	int mid=(l+r)/2;
	if (k<=mid) update(l,mid,k,val,tr[pre].ls,tr[nod].ls);//更新的节点在左子树，所以当前节点的左儿子是要新建的
	else update(mid+1,r,k,val,tr[pre].rs,tr[nod].rs); //更新的节点在右子树，所以当前节点的右儿子是要新建的

现在如果我们要新建一个版本是在版本v的基础上更新出来的，我们可以在主程序中这样写：
（显然rt[v]是rt[++cnt]的前驱，cnt是当前版本数）

update(1,n,k,val,rt[v],rt[++cnt]);

然后query的部分和原来就是完全一样的：

int query(int l,int r,int k,int nod){
	if (l==r) return tr[nod].v;
	int mid=(l+r)/2;
	if (k<=mid) return query(l,mid,k,tr[nod].ls);
	else return query(mid+1,r,k,tr[nod].rs); 
}

如果我们要查询版本v上的某一个值主程序长这样：
（版本v这棵线段树的根节点就是rt[v]，So，我们从rt[v]出发）

printf("%d\n",query(1,n,k,rt[v]));

这道题就被我们切掉了

（【洛谷P3919】【模板】可持久化数组）C++代码：

#include
using namespace std;

const int maxn=1000005;

struct Tree{
	int ls,rs,v;
}tr[maxn*35];

int n,m;
int a[maxn],rt[maxn],cnt=0,tot=0;

void build(int l,int r,int &nod){
	nod=++tot;
	if (l==r){
		tr[nod].v=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(l,mid,tr[nod].ls);
	build(mid+1,r,tr[nod].rs);
}

void update(int l,int r,int k,int val,int pre,int &nod){
	nod=++tot;
	tr[nod]=tr[pre];
	if (l==r){
		tr[nod].v=val;
		return;
	}
	int mid=(l+r)/2;
	if (k<=mid) update(l,mid,k,val,tr[pre].ls,tr[nod].ls);
	else update(mid+1,r,k,val,tr[pre].rs,tr[nod].rs); 
}

int query(int l,int r,int k,int nod){
	if (l==r) return tr[nod].v;
	int mid=(l+r)/2;
	if (k<=mid) return query(l,mid,k,tr[nod].ls);
	else return query(mid+1,r,k,tr[nod].rs); 
}

int main(){
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	build(1,n,rt[0]);
	while(m--){
		int v,opt,k,val;
		scanf("%d%d",&v,&opt);
		if (opt==1){
			scanf("%d%d",&k,&val);
			update(1,n,k,val,rt[v],rt[++cnt]);
		}
		else{
			scanf("%d",&k);
			printf("%d\n",query(1,n,k,rt[v]));
			rt[++cnt]=rt[v];
		}
	}
	return 0;
}

---

接下来我们再来看一道用可持久化线段树解决的经典的问题：静态区间第K小

我们先来思考一下怎么用普通的线段树解决整个序列的第k小

“排序以后输出第k个”（请不要砸场 ，想想线段树怎么搞）

我们要注意到n的范围相对较小，$a_i$的范围较大，而且我们只关心每一个$a_i$的排名，So，我们完全可以对$a_i$进行离散化，假设现在的a数组是我们已经离散好了的，那么我们是不是可以用叶子节点为它建一个桶，线段树上的每个节点[l,r]表示权值再区间[l,r]里的数的个数（维护的就是两个儿子的和）

我们在query第k小的时候走到当前节点[l,r]，看一看左子树的值和k的大小关系，如果左子树的值>=k，就说明说在区间[l,mid]里面的数比k多，那么第k小的数一定在左区间，如果左子树的值

走到叶子节点l=r时，l就是答案

int query(int l,int r,int k,int nod){
	if (l==r) return l;
	int mid=(l+r)/2;
	int tmp=tr[tr[nod].ls].v;
	if (k<=tmp) return query(l,mid,k,tr[nod].ls);
	else return query(mid+1,r,k-tmp,tr[nod].rs);
}

但是现在的查询区间[l,r]不是固定的怎们办呢？我们可不可以搞一个类似前缀和的东西来解决这个问题：

我们对每一个下标区间[1,i]建一棵上面说的那种线段树，建好以后，如果我们要查询的区间是[l,r]（这里的l和r是下标的，而不是权值的，不要弄混了），虽然这个区间的线段树我们可能没有建过，但是我们可以在脑子里面想象一下这颗线段树的样子，这颗线段树节点nod上的值就是区间[1,r]那颗线段树对应节点上的值减去区间[1,l-1]那颗线段树对应节点上的值

然后就被我们解决了

但是这要建n棵线段树咧！无论是时间还是空间都是承受不住的呀！

这不是上面刚刚学完可持久化线段树吗！

我们来看区间[1,i]和区间[1,i+1]这两颗线段树是不是只有一条链是不一样的，就是a[i+1]这个数的贡献，会在$[a_{i+1},a_{i+1}]$这个叶子节点上++，既然只有一条链是不一样的，那我们就把i作为i+1的前驱update开一条链出来就行了

---

（【洛谷P3834】【模板】可持久化线段树 1（主席树））c++代码：

#include
using namespace std;

const int maxn=500005;

struct Tree{
    int ls,rs,v;
}tr[maxn*35];

int n,m,tot=0;

int rt[maxn],a[maxn],b[maxn];

void pushup(int nod){
    tr[nod].v=tr[tr[nod].ls].v+tr[tr[nod].rs].v;
}

void update(int l,int r,int k,int val,int pre,int &nod){
    nod=++tot;
    tr[nod]=tr[pre];
    if (l==r){
        tr[nod].v+=val;
        return;
    }
    int mid=(l+r)/2;
    if (k<=mid) update(l,mid,k,val,tr[pre].ls,tr[nod].ls);
    else update(mid+1,r,k,val,tr[pre].rs,tr[nod].rs);
    pushup(nod);
}

int query(int l,int r,int k,int nodl,int nodr){
    if (l==r) return l;
    int mid=(l+r)/2;
    int tmp=tr[tr[nodr].ls].v-tr[tr[nodl].ls].v;
    if (k<=tmp) return query(l,mid,k,tr[nodl].ls,tr[nodr].ls);
    else return query(mid+1,r,k-tmp,tr[nodl].rs,tr[nodr].rs);
}

int main(){
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        b[i]=a[i];
    }
    sort(b+1,b+n+1);
    int num=unique(b+1,b+n+1)-b-1;
    rt[0]=0;
    for (int i=1;i<=n;i++){
        int k=lower_bound(b+1,b+num+1,a[i])-b;
        update(1,num,k,1,rt[i-1],rt[i]);
    }
    while(m--){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        int tmp=query(1,num,k,rt[l-1],rt[r]);
        printf("%d\n",b[tmp]);
    }
    return 0;
} 

OK，完事

感谢chhokmah大佬的讲解

于HG机房