GAN的Loss的比较研究（4）——Wasserstein Loss理解（2）

关于Wasserstein Distance的计算，似乎还有一个简单一点的推导方法，在《BEGAN: Boundary Equilibrium Generative Adversarial Networks》中给出了一个推导的过程：
Wasserstein Distance的定义式如下：

W(ℙr,ℙg)=infγ∈Π(ℙr,ℙg)E(x,y)∼γ[‖x−y‖](1) W ( P r , P g ) = inf γ ∈ Π ( P r , P g ) E ( x , y ) ∼ γ [ ‖ x − y ‖ ] ( 1 )

根据Jensen不等式有：

infE[|x1−x2|]≥inf|E[x1−x2]|=|E(x1)−E(x2)|(2) inf E [ | x 1 − x 2 | ] ≥ inf | E [ x 1 − x 2 ] | = | E ( x 1 ) − E ( x 2 ) | ( 2 )

于是代入（1）有：

W(ℙr,ℙg)≥|Ex∼ℙr(fθ(x))−Ex∼ℙg(fθ(x))|=|m1−m2|(3) W ( P r , P g ) ≥ | E x ∼ P r ( f θ ( x ) ) − E x ∼ P g ( f θ ( x ) ) | = | m 1 − m 2 | ( 3 )

fθ(x) f θ ( x ) 表示由判别器（Discriminator）决定的映射，不同分布的随机变量（ x∼ℙr x ∼ P r 和 x∼ℙg x ∼ P g ）经过 fθ(x) f θ ( x ) 映射后，就可得到要比较的分布。通过求这两个变换随机分布的均值差的绝对值（1次范数），定义这两个变换分布的距离。对于判别器而言，我们希望（3）越大越好，在判别器达到最优时，若真图判别都比假图判别大，这样可以去掉绝对值符号，就有（4）：

W(ℙr,ℙg)≥Ex∼ℙr(fθ(x))−Ex∼ℙg(fθ(x))(4) W ( P r , P g ) ≥ E x ∼ P r ( f θ ( x ) ) − E x ∼ P g ( f θ ( x ) ) ( 4 )

最大化（4）可定义Loss_D（取反，求最小值），生成器的Loss_G与此作用相反，取反号，并去掉无关项，有如下（5）~(8）：

Loss_D=−Ex∼ℙr(fθ(x))+Ex∼ℙg(fθ(x))(5)θ∗=argminθLoss_D(6) L o s s _ D = − E x ∼ P r ( f θ ( x ) ) + E x ∼ P g ( f θ ( x ) ) ( 5 ) θ ∗ = arg ⁡ min θ L o s s _ D ( 6 )

Loss_G=−Ex∼ℙg(fθ(x))=−Ez∼ℤ(fθ(gω(x))(7)ω∗=argminωLoss_G(8) L o s s _ G = − E x ∼ P g ( f θ ( x ) ) = − E z ∼ Z ( f θ ( g ω ( x ) ) ( 7 ) ω ∗ = arg ⁡ min ω L o s s _ G ( 8 )

以上计算过程与上一篇文章 《GAN的Loss的比较研究（3）——Wasserstein Loss理解（1）》的（5）、（6）是相同，但注意在这个推导过程中，没有对 fθ(x) f θ ( x ) 有任何要求。

以上过程可以小结如下：
真图的概率分布是 ℙr P r ，假图的概率分布是 ℙg P g ，用判别器（Discriminator）将其映射到另一个概率分布空间，然后用两个分布的重心之间的距离来衡量距离。如下图：

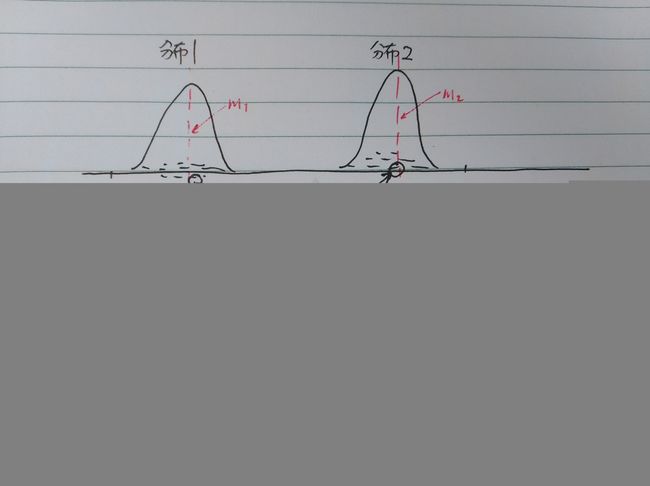
上图的解释如下： ℙr P r 抽样得到 xr x r ，它经过映射 fθ(⋅) f θ ( ⋅ ) 变换到[0,1]上，然后计算这部分样本映射后的均值，也就是分布2的重心 m2 m 2 ，同理，对于假图亦如此处理。

这个过程推导没问题，也简单许多，但实际训练时，生成器（Generator）却无法收敛。因为， ℙr P r 和 ℙg P g 流型根本可能是不连通的，即Discriminator可以很早就训练成了最优判别器，无法给Generator提供后向的梯度信息，与前述的KL距离不能收敛的问题原因是一致的。仔细比较本文的公式(5)与上一篇（《Wasserstein Loss理解（1）》）的公式（6），差异仅仅在对 fθ(x) f θ ( x ) 有没有约束，前文是有约束的： fθ(x) f θ ( x ) 必须满足Lipschitz条件，而本文中（5）并无要求，这个要求就是是否收敛的关键。
解决了这个问题，又出现了新问题：为什么《BEGAN: Boundary Equilibrium Generative Adversarial Networks》就可以收敛呢？
BEGAN与一般的GAN的结构不同，如下图：

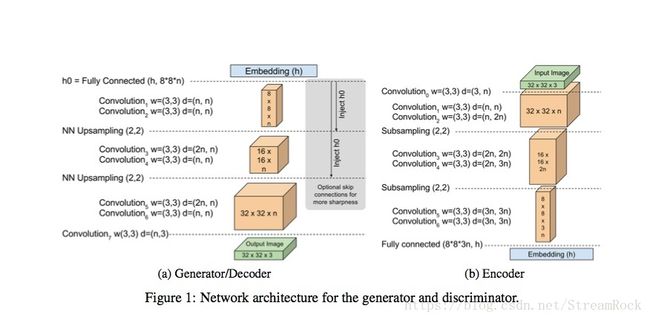
它的判别器（Discriminator）由Auto-Encoder实现，编码得到的Embedding (h)与生成器（Generator）的输入随机变量是同维度的，是不是由于Auto-Encoder压缩了两个随机分布（ ℙr P r 和 ℙg P g ）的维度，将两个随机分布(即：由真图经过判别器的Encoder生成的真图Code的分布 ℙRealCode P R e a l C o d e ，以及由假图经过Encoder生成的假图Code的分布 ℙFakeCode P F a k e C o d e )的流型变成了有重叠的部分，从而使简单的两分布概率重心距离可以作为分布差异的度量？判别器的Auto-Encoder就像是生成器的引导器，将生成器生成空间的流型引导到真实图像空间流型上去，而且再进一步压缩维度，使两者的Code的流型进一步接近，为它们有部分重合提供了有力的支持，如下：

上图中红框内C表示的就是图像经过Encoder后得到的Code，真图Code与假图Code的流型若是重叠的，则可能可以完成分布的迁移。
另外，能令BEGAN收敛，以及多样性的还有一条措施，就是反馈比例控制，如下：

(x)=|x−D(x)|(9)D=(x)−kt⋅(G(zD))(10)G=(G(zG))(11)kt+1=kt+λk(γ(x)−(G(zG)))(12) L ( x ) = | x − D ( x ) | ( 9 ) L D = L ( x ) − k t ⋅ L ( G ( z D ) ) ( 10 ) L G = L ( G ( z G ) ) ( 11 ) k t + 1 = k t + λ k ( γ L ( x ) − L ( G ( z G ) ) ) ( 12 )

因为判别器是Auto-Encoder，其输出是与输入相同维度的图像，（9）表示Auto-Encoder的输入与输出的差的范数， D L D 表示判别器的Loss， G L G 表示生成器的Loss， zG和zD z G 和 z D 都是生成器的噪声输入，前者是求 G L G 时的抽样，后者是求 D L D 的抽样。
（10）和（12）中 (x) L ( x ) 表示从真图中采样，Auto-Encoder输入与输出的差，而 (G(z)) L ( G ( z ) ) 表示生成器根据噪声激励产生的假图送人Auto-Encoder，输入和输出的差异。（12）反映的是输入是真图和假图条件下，Auto-Encoder范数的差异，即原图恢复的好坏程度。如果没有什么差异，则要增强判别器作为Auto-Encoder对真图的恢复能力，如果差异大，则要增加判别器的区分真假的判别功能。通过 kt k t 的反馈比例控制，实现了上述的均衡的目的。