1 线段树的定义
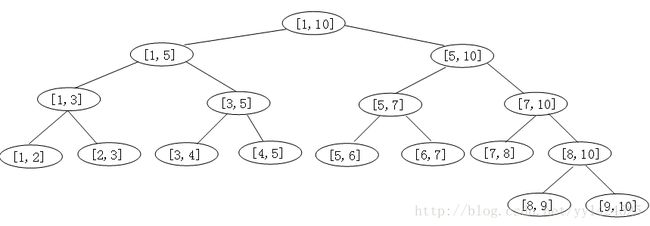
首先,线段树是一棵二叉树。它的特点是:每个结点表示的是一个线段,或者说是一个区间。事实上,一棵线段树的根结点表示的是“整体”区间,而它的左右子树也是一棵线段树,分别表示区间的左半边和右半边。树中的每个结点表示一个区间[a,b]。每一个叶子结点表示一个单位区间。对于每一个非叶结点所表示的结点[a,b],其左孩子表示的区间为[a,(a+b)/2],右孩子表示的区间为[(a+b)/2,b]。 用T(a, b)表示一棵线段树,参数a,b表示区间[a,b],其中b-a称为区间的长度,记为L。
线段树主要用于高效解决连续区间的动态查询问题,由于二叉结构的特性,使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
代码如下:
public class SegmentTree {
private E[] data;
private E[] tree;
private Merger merger;
public SegmentTree(E[] arr, Merger merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++)
data[i] = arr[i];
tree = (E[]) new Object[4 * arr.length];// 开启一个四倍大小的新数组
buildSegmentTree(0, 0, arr.length - 1);
}
private void buildSegmentTree(int treeIndex, int l, int r) {
if (l == r) {
// 代表当前这个treeIndex再没有左右子节点了,直接赋值吧
tree[treeIndex] = data[r];
return;
}
// 否则继续找到index的左右子树,继续遍历
int mid = (l + r) / 2;
int lChild = leftChild(treeIndex);
int rChild = rightChild(treeIndex);
buildSegmentTree(lChild, l, mid);
buildSegmentTree(rChild, mid + 1, r);
// 需要把俩边的子树的值加起来
tree[treeIndex] = merger.merge(tree[lChild], tree[rChild]);
}
public int getSize() {
return data.length;
}
public E get(int index) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal.");
return data[index];
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index) {
return 2 * index + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index) {
return 2 * index + 2;
}
public static void main(String[] args) {
Integer[] nums = { -2, 0, 3, -5, 2, -1 };
SegmentTree segTree = new SegmentTree<>(nums,
new Merger() {
@Override
public Integer merge(Integer a, Integer b) {
return a + b;
}
});
System.out.println(segTree);
System.out.println(segTree.query(1, 3));
segTree.set(1, 1);
System.out.println(segTree.query(1, 3));
}
// 返回区间[queryL, queryR]的值
public E query(int queryL, int queryR) {
if (queryL < 0 || queryL >= data.length || queryR < 0
|| queryR >= data.length || queryL > queryR)
throw new IllegalArgumentException("Index is illegal.");
return query(0, 0, data.length - 1, queryL, queryR);
}
// 在以treeIndex为根的线段树中[l...r]的范围里,搜索区间[queryL...queryR]的值
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
// treeIndex 二叉树的节点的下标
// l,r线段树每个节点代表的区间
if (l == queryL && r == queryR) {
return tree[treeIndex];
}
int mid = (l + r) / 2;
int lChild = leftChild(treeIndex);
int rChild = rightChild(treeIndex);
if (queryL > mid) {
return query(rChild, mid + 1, r, queryL, queryR);
} else if (queryR < mid + 1) {
return query(lChild, l, mid, queryL, queryR);
}
// 如果上面俩都没进去的话,代表当前的查询区间融合了左右子树
// 这个时候我们需要两边都分别的查询一下,然后汇总
E lRes = query(lChild, l, mid, queryL, mid);
E rRes = query(rChild, mid + 1, r, mid + 1, queryR);
return merger.merge(lRes, rRes);
}
// 将index位置的值,更新为e
public void set(int index, E e) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal");
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
// 在以treeIndex为根的线段树中更新index的值为e
private void set(int treeIndex, int l, int r, int index, E e) {
if (l == r) {
// 代表当前的treeindex就是index了
tree[treeIndex] = e;
return;
}
int mid = (l + r) / 2;
int lChild = leftChild(treeIndex);
int rChild = rightChild(treeIndex);
if (index > mid) {
set(rChild, mid + 1, r, index, e);
} else {
set(lChild, l, mid, index, e);
}
tree[treeIndex] = merger.merge(tree[lChild], tree[rChild]);
}
}