刘汝佳《算法竞赛入门经典(第二版)》习题(六)
刘汝佳《算法竞赛入门经典(第二版)》第四章习题(4-1~4-3)
习题4-1 象棋(Xiangai,ACM/ICPC Fuzhou 2011,UVa1589)
考虑一个象棋残局,其中红方有n(2≤n≤7)个旗子,黑方只有一个将。红方除了有一个帅(G)之外还有3种可能的棋子:车(R),马(H),炮(C),并且需要考虑“蹩马腿”与将和帅不能照面(将、帅如果同在一条直线上,中间又不隔着任何棋子的情况下,先走的一方获胜)的规则。
输入所有棋子的位置,保证局面合法并且红方已经将军。你的任务是判断红方是否已经把黑方将死。关于中国象棋的相关规则请参见原题。
原题描述
Description
Xiangqi is one of the most popular two-player board games in China. The game represents a battle between two armies with the goal of capturing the enemy’s “general” piece. In this problem, you are given a situation of later stage in the game. Besides, the red side has already “delivered a check”. Your work is to check whether the situation is “checkmate”.
Now we introduce some basic rules of Xiangqi. Xiangqi is played on a 10×9 board and the pieces are placed on the intersections (points). The top left point is (1,1) and the bottom right point is (10,9). There are two groups of pieces marked by black or red Chinese characters, belonging to the two players separately. During the game, each player in turn moves one piece from the point it occupies to another point. No two pieces can occupy the same point at the same time. A piece can be moved onto a point occupied by an enemy piece, in which case the enemy piece is “captured” and removed from the board. When the general is in danger of being captured by the enemy player on the enemy player’s next move, the enemy player is said to have “delivered a check”. If the general’s player can make no move to prevent the general’s capture by next enemy move, the situation is called “checkmate”.
We only use 4 kinds of pieces introducing as follows:
General: the generals can move and capture one point either vertically or horizontally and cannot leave the “palace” unless the situation called “flying general” (see the figure above). “Flying general” means that one general can “fly” across the board to capture the enemy general if they stand on the same line without intervening pieces.
Chariot: the chariots can move and capture vertically and horizontally by any distance, but may not jump over intervening pieces
Cannon: the cannons move like the chariots, horizontally and vertically, but capture by jumping exactly one piece (whether it is friendly or enemy) over to its target.
Horse: the horses have 8 kinds of jumps to move and capture shown in the left figure. However, if there is any pieces lying on a point away from the horse horizontally or vertically it cannot move or capture in that direction (see the figure below), which is called “hobbling the horse sleg”.
Now you are given a situation only containing a black general, a red general and several red chariots, cannons and horses, and the red side has delivered a check. Now it turns to black side’s move. Your job is to determine that whether this situation is “checkmate”.
Input
The input contains no more than 40 test cases. For each test case, the first line contains three integers representing the number of red pieces N (2<=N<=7) and the position of the black general. The following n lines contain details of N red pieces. For each line, there are a char and two integers representing the type and position of the piece (type char ‘G’ for general, ‘R’ for chariot, ‘H’ for horse and ‘C’ for cannon). We guarantee that the situation is legal and the red side has delivered the check.
There is a blank line between two test cases. The input ends by 0 0 0.
样例输入和样例输出:
解析:
思路很简单,对于黑方将所有可行的下一步棋,红方的所有棋子都进行模拟攻击,根据攻击结果判断红方是否已经把黑方将死(或者按棋盘来进行搜索也可以AC,毕竟棋盘只有10行9列,应该不会超时,但明显是按棋子搜索更好,因为棋子最多只有7个)。思路不难但坑点很多:
1.小心棋盘越界。
2.将和帥的活动范围只有r行c列(1≤r≤3,4≤c≤6),对将的当前位置,对应的下一步位置以及路线数量都不同。
3.馬能否进行攻击的条件比较特殊,需要仔细考虑。
4.红方棋子相对于黑方将的位置不同,攻击路线也有所不同。
5.将与帥不能处在可以攻击对方的位置,否则红方必输。
(以为完了?想太多了…)
6.由于下一步是黑方走,因此要考虑到帥可能会吃掉红方(除将外)的棋子,而红方少一个棋子后不一定就将不死黑方(很多人死在这一点上)。
上述坑点都要考虑到,不然写的代码即使测试用例过了也还是会WA(或者拿不到满分)。
下面的代码并不是标准的比赛代码,因为虽然策略优,但是代码量较大,为了优化程序运行时间(其实这种思路对于这道题大可不必,我强迫症- -)添加了很多代码。主要看各函数的功能就行(代码注释讲得很清楚):
源代码:
#include
#include
using namespace std;
char chess[11][10];//棋盘
const int movH[8][2] = {{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2},{-2,-1},{-2,1}};//馬的走位
//棋子
struct Chess
{
char type;
int x;
int y;
};
//由馬的走位推出“馬脚”的位置
int isMove (int i)
{
if(i > 0)
return -1;
else if (i < 0)
return 1;
else
return 0;
}
//帥的攻击路线
bool G (int x, int y, int target_x, int target_y)
{
int i;
if (y != target_y)//如果帥与目标不在同一纵轴上,则必定无法攻击成功
return false;
//将的攻击路线上是否有别的棋子
for (i = x-1; i > target_x; i--)
if (isalpha(chess[i][y]))
return false;
return true;
}
//車的攻击路线
bool R (int x, int y, int target_x, int target_y)
{
int i;
if (x != target_x && y != target_y)
return false;
else
{
//按照車在敌方将的上下左右四个位置有不同的攻击路线(炮也一样)
if (x == target_x)
{
if (y < target_y)//車在将的左边
for (i = y+1; i <= target_y; i++)
{
if (isalpha(chess[x][i]))
return false;
else
continue;
}
else if (y > target_y)//車在将的右边
for (i = y-1; i >= target_y; i--)
{
if (isalpha(chess[x][i]))
return false;
else
continue;
}
}
else if (y == target_y)
{
if (x < target_x)//車在将的上方
for (i = x+1; i <= target_x; i++)
{
if (isalpha(chess[i][y]))
return false;
else
continue;
}
else if (x > target_x)//車在将的下方
for (i = x-1; i >= target_x; i--)
{
if (isalpha(chess[i][y]))
return false;
else
continue;
}
}
}
return true;
}
//馬的攻击路线
bool H (int x, int y, int target_x, int target_y)
{
int i;
for (i = 0; i < 8; i++)
if (x+movH[i][0] == target_x && y+movH[i][1] == target_y)
if (!isalpha(chess[i+isMove(movH[i][0])][i+isMove(movH[i][1])]))//“馬脚”处是否有棋子
return true;
return false;
}
//炮的攻击路线
bool C (int x, int y, int target_x, int target_y)
{
int i,cnt = 0;
if (x != target_x && y != target_y)
return false;
else
{
if (x == target_x)
{
if (y < target_y)
for (i = y+1; i <= target_y; i++)
{
if (isalpha(chess[x][i]))
cnt++;
else
continue;
}
else if (y > target_y)
for (i = y-1; i >= target_y; i--)
{
if (isalpha(chess[x][i]))
cnt++;
else
continue;
}
}
else if (y == target_y)
{
if (x < target_x)
for (i = x+1; i <= target_x; i++)
{
if (isalpha(chess[i][y]))
cnt++;
else
continue;
}
else if (x > target_x)
for (i = x-1; i >= target_x; i--)
{
if (isalpha(chess[i][y]))
cnt++;
else
continue;
}
}
}
if (cnt == 1)//炮与攻击目标之间有且只有一个棋子才能攻击成功
return true;
else
return false;
}
//红方所有棋子分别对目标位置进行攻击
bool isKill (Chess* p, int n, int target_x, int target_y)
{
int cnt = 0;
for (int i = 0; i < n; i++)
{
if (p[i].type == 'G')
{
if (G(p[i].x, p[i].y, target_x, target_y))
cnt++;
}
else if (p[i].type == 'R')
{
if (R(p[i].x, p[i].y, target_x, target_y))
cnt++;
}
else if (p[i].type == 'C')
{
if (C(p[i].x, p[i].y, target_x, target_y))
cnt++;
}
else if (p[i].type == 'H')
{
if (H(p[i].x, p[i].y, target_x, target_y))
cnt++;
}
else
continue;
}
if (cnt && !isalpha(chess[target_x][target_y]))
return true;
else if (isalpha(chess[target_x][target_y]) && cnt > 1)//若黑方将的下一步会吃掉红方一棋子(不包括将与帥之间的攻击),那么红方必须有其他棋子能成功进行下一步攻击
return true;
else
return false;
}
int main (void)
{
char c;
int n,t_x,t_y;
while ((cin >> n >> t_x >> t_y) && n && t_x && t_y)
{
memset(chess, '*', sizeof(chess));
Chess* p = new Chess[7];
chess[t_x][t_y] = 'g';
int i,x,y;
for (i = 0; i < n; i++)
{
cin >> c >> x >> y;
chess[x][y] = c;
p[i].type = c;
p[i].x = x;
p[i].y = y;
}
bool way1 = true, way2 = true, way3 = true, way4 = true;
//先对帥的位置进行判断,如果将与帥处于可以互相攻击的位置,那么红方必输
for (i = 0; i < n; i++)
if (p[i].type == 'G')
if (G(p[i].x, p[i].y, t_x, t_y))
{
cout << "NO\n";
return 0;
}
//对黑方"将"所有可行的下一步棋进行模拟攻击
if (t_x-1 >= 1)
{
way1 = false;
if (isKill(p, n, t_x, t_y-1))
way1 = true;
}
if (t_x+1 <= 3)
{
way2 = false;
if (isKill(p, n, t_x, t_y+1))
way2 = true;
}
if (t_y-1 >= 4)
{
way3 = false;
if (isKill(p, n, t_x-1, t_y))
way3 = true;
}
if (t_y+1 <= 6)
{
way4 = false;
if (isKill(p, n, t_x+1, t_y))
way4 = true;
}
if (way1 && way2 && way3 && way4)
cout << "YES\n";
else
cout << "NO\n";
delete []p;
}
return 0;
} 运行结果:
习题4-2正方形(Squares,ACM/ICPC World Finals 1990,UVa201)
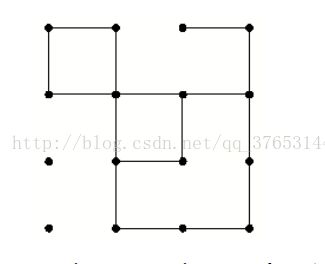
有n行n列(2≤n≤9)的小圆点,还有m条线段连接其中的一些黑点。统计这些线段连成了多少个正方形(每种边长分别统计)。
行从上到下编号为1~n,列从左到右编号为1~n。边用Hij和Vij表示,分别代表边(i,j)-{i,j+1}和(i,j)-(i+1,j)。
原题描述
A children’s board game consists of a square array of dots that contains lines connecting some of the pairs of adjacent dots. One part of the game requires that the players count the number of squares of certain sizes that are formed by these lines. For example, in the figure shown below, there are 3 squares — 2 of size 1 and 1 of size 2. (The “size” of a square is the number of lines segments required to form a side.)
Your problem is to write a program that automates the process of counting all the possible squares.
Input
The input file represents a series of game boards. Each board consists of a description of a square array of n2 dots (where 2 ≤ n ≤ 9) and some interconnecting horizontal and vertical lines. A record for a single board with n2 dots and m interconnecting lines is formatted as follows:
Line 1: n the number of dots in a single row or column of the array Line 2: m the number of interconnecting lines
Each of the next m lines are of one of two types:
Hij indicates a horizontal line in row i which connects
the dot in column j to the one to its right in column j +1
or
Vij indicates a vertical line in column i which connects
the dot in row j to the one below in row j + 1
Information for each line begins in column 1. The end of input is indicated by end-of-file. The first
record of the sample input below represents the board of the square above.
Output
For each record, label the corresponding output with ‘Problem #1’, ‘Problem #2’, and so forth. Output for a record consists of the number of squares of each size on the board, from the smallest to the largest. lf no squares of any size exist, your program should print an appropriate message indicating so. Separate output for successive input records by a line of asterisks between two blank lines, like in the sample below.
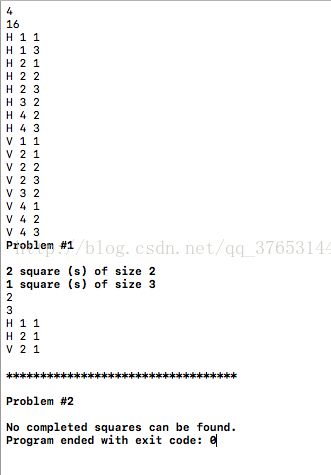
样例输入和样例输出:
解析:
扫描起始点(以正方形的左上角为起始点),判断正方形的横边和竖边是否缺失。除了输出格式有较多要求外这道题没什么难度。
如果在不超时的情况下不在意那点运行时间的话,直接扫描所有点即可,但会扫描到很多一开始就不可能构成正方形的点。比如有4行4列的点,对于边长为2的正方形来说,只需要扫描前两行和前两列即可,因为以其余的点为起始点,即使有边也不可能构成边长为2的正方形。
源代码:
#include
using namespace std;
int H[10][10];
int V[10][10];
int judge (int len, int n)
{
int sum = 0, num = n/len;
for (int i = 1; i < num+1; i++)
for (int j = 1; j < num+1; j++)
{
int k;
bool ok = true;
for (k = j; k < j+num; k++)
if (!H[i][k] && !H[i+num][k])
{
ok = false;
break;
}
for (k = i; k < i+num; k++)
if (!V[k][j] && !V[k][j+num])
{
ok = false;
break;
}
if (ok)
sum++;
}
return sum;
}
int main (void)
{
int n,m,kase = 1;
while (cin >> n >> m)
{
int i,j,k;
char c;
memset(H, 0, sizeof(H));
memset(V, 0, sizeof(V));
for (k = 0; k < m; k++)
{
cin >> c >> i >> j;
if (c == 'H')
H[i][j] = 1;
else if (c == 'V')
V[i][j] =1;
else
continue;
}
if (kase-1)
cout << "\n**********************************\n\n";
cout << "Problem #" << kase++ << endl << endl;
int len = 1,cnt = 0;
while (len < n)
{
if (judge(len, n))
{
cnt++;
cout << judge(len, n) << " square (s) of size " << len << endl;
}
len++;
}
if (!cnt)
cout << "No completed squares can be found.\n";
}
return 0;
} 运行结果:
习题4-3黑白格(Othello ,ACM/ICPC World Finals 1992,UVa220)
你的任务是模拟黑白棋游戏的进程。黑白棋的规则为:黑白双方轮流放棋子,每次必须让新放的棋子“夹住”至少一枚对方棋子,然后把所有被新放棋子“夹住”的对方棋子替换成己方棋子。一段连续(横、竖或者斜向)的同色棋子被“夹住”的条件是两端都是对方棋子(不能是空位)。
输入一个8*8的棋盘以及当前下一次操作的游戏者,处理3种指令:
1.L指令打印所有合法操作,按照从上到下,从左到右的顺序排列(没有合法操作时输出No legal move)。
2.Mrc指令放一枚棋子在(r,c)。如果当前游戏者没有合法操作,则是先切换游戏者再操作。输入保证这个操作是合法的。输出操作完毕后黑白方的棋子总数。
3.Q指令退出游戏,并打印当前棋盘(格式同输入)。
原题描述
Othello is a game played by two people on an 8 x 8 board, using disks that are white on one side andblack on the other. One player places disks with the white side up and the other player places diskswith the black side up. The players alternate placing one disk on an unoccupied space on the board.In placing a disk, the player must bracket at least one of the other color disks. Disks are bracketedif they are in a straight line horizontally, vertically, or diagonally, with a disk of the current player’scolor at each end of the line. When a move is made, all the disks that were bracketed are changed tothe color of the player making the move. (It is possible that disks will be bracketed across more thanone line in a single move.)
Input
The first line of the input is the number of games to be processed. Each game consists of a boardconfiguration followed by a list of commands. The board configuration consists of 9 lines. The first 8specify the current state of the board. Each of these 8 lines contains 8 characters, and each of thesecharacters will be one of the following:
‘-’ indicating an unoccupied square
‘B’ indicating a square occupied by a black disk
‘W’ indicating a square occupied by a white disk
The ninth line is either a ‘B’ or a ‘W’ to indicate which is the current player. You may assume thatthe data is legally formatted.
Then a set of commands follows. The commands are to list all possible moves for the current player,make a move, or quit the current game. There is one command per line with no blanks in the input.
Output
The commands and the corresponding outputs are formatted as follows:
List all possible moves for the current player.The command is an ‘L’ in the first column of theline. The program should go through the board and print all legal moves for the current playerin the format (x, y) where x represents the row of the legal move and y represents its column.These moves should be printed in row major order which means:
1) all legal moves in row number i will be printed before any legal move in row number j if jis greater than iand
2) if there is more than one legal move in row number i, the moves will be printed in ascendingorder based on column number.
All legal moves should be put on one line. If there is no legal move because it is impossible for thecurrent player to bracket any pieces, the program should print the message ‘No legal move.’
Make a move. The command is an ‘M’ in the first column of the line, followed by 2 digits in thesecond and third column of the line. The digits are the row and the column of the space to placethe piece of the current player’s color, unless the current player has no legal move. If the currentplayer has no legal move, the current player is first changed to the other player and the movewill be the move of the new current player. You may assume that the move is then legal. Youshould record the changes to the board, including adding the new piece and changing the colorof all bracketed pieces. At the end of the move, print the number of pieces of each color on theboard in the format ‘Black - xx White - yy’ where xx is the number of black pieces on theboard and yy is the number of white pieces on the board. After a move, the current player willbe changed to the player that did not move.
Quit the current game. The command will be a ‘Q’ in the first column of the line. At this point,print the final board configuration using the same format as was used in the input. This terminatesinput for the current game.
You may assume that the commands will be syntactically correct. Put one blank line betweenoutput from separate games and no blank lines anywhere else in the output.
样例输入和样例输出:
Sample Input
2
--------
--------
--------
---WB---
---BW---
--------
--------
--------
W
L
M35
L
Q
WWWWB---
WWWB----
WWB-----
WB------
--------
--------
--------
--------
B
L
M25
L
Q
Sample Output
(3,5) (4,6) (5,3) (6,4)
Black - 1 White - 4
(3,4) (3,6) (5,6)
--------
--------
----W---
---WW---
---BW---
--------
--------
--------
No legal move.
Black - 3 White - 12
(3,5)
WWWWB---
WWWWW---
WWB-----
WB------
--------
--------
--------
--------
解析:
遍历棋盘,以一棋子为中心有8条路线,根据路线按题目要求写即可。这类题目都是思路简单但细节处理比较繁琐。对于这类题目最好是将问题细分,采用模块化编程来做,不然就只有一大坨代码的话,上个厕所回来都不记得分析到哪了……
源代码:
#include
#include
#include
#include
using namespace std;
char chess[10][10];
//判断坐标是否合法操作
bool isLegal (char player, int r, int c)
{
char con = '\0';
bool ok = false;
int next[8][2] = {{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1},{0,-1},{-1,-1}};
if (player == 'B')
con = 'W';
else if (player == 'W')
con = 'B';
for (int i = 0; i < 8; i++)
{
int x = r+next[i][0], y = c+next[i][1];
if (x >= 1 && x <= 8 && y >= 1 && y <= 8 && chess[x][y] == con)//判断相邻位置是否存在与目标棋子不同的棋子
{
x += next[i][0], y += next[i][1];
while (x >= 1 && x <= 8 && y >= 1 && y <= 8)//在第一层基础上往一个方向找下去,判断是否存在与目标棋子相同的棋子
{
if (!isalpha(chess[x][y]))//若中间有空缺则不合法
break;
else if (chess[x][y] == player)
{
ok = true;
break;
}
x += r+next[i][0], y += c+next[i][1];
}
if (ok)
break;
}
else
continue;
}
return ok;
}
//L指令
void L (char &player)
{
int i, j, sum = 0;
bool first = true;
//扫描棋盘(从上到下,从左到右),找出合法操作的坐标并输出
for (i = 1; i <= 8; i++)
for (j = 1; j <= 8; j++)
{
if (!isalpha(chess[i][j]) && isLegal(player, i, j))
{
if (first)
{
cout << "(" << i << "," << j << ")";
first = false;
}
else
cout << " (" << i << "," << j << ")";
sum++;
}
}
if (!sum)
{
cout << "No legal move.\n";
if (player == 'B')
player = 'W';
else if (player == 'W')
player = 'B';
}
else
cout << endl;
}
//M指令
void M (char &player, int r, int c)
{
char con = '\0';
int i, j;
if (player == 'B')
con = 'W';
else if (player == 'W')
con = 'B';
// if (!isLegal(player, r, c))
// {
// if (player == 'B')
// player = 'W';
// else if (player == 'W')
// player = 'B';
// }
chess[r][c] = player;//落子
int next[8][2] = {{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1},{0,-1},{-1,-1}};//8个落子方向
for (i = 0; i < 8; i++)
{
int x = r+next[i][0], y = c+next[i][1];
if (x >= 1 && x <= 8 && y >= 1 && y <= 8 && chess[x][y] == con)//查找相邻位置(第1圈)
if (x+next[i][0] >= 1 && x+next[i][0] <= 8 && y+next[i][1] >= 1 && y+next[i][1] <= 8 && chess[x+next[i][0]][y+next[i][1]] == player)//查找次相邻位置(第2圈)
{
chess[x][y] = player;
break;
}
}
//统计黑白棋子数
int B = 0, W = 0;
for (i = 1; i <= 8; i++)
for (j = 1; j <= 8; j++)
{
if (chess[i][j] == 'B')
B++;
else if (chess[i][j] == 'W')
W++;
else
continue;
}
if (player == 'B')
player = 'W';
else if (player == 'W')
player = 'B';
cout << "Black -" << setw(2) << B << " White -" << setw(2) << W << endl;
}
//Q指令
void Q (void)
{
int i, j;
//打印当前棋盘
for (i = 1; i <= 8; i++)
{
int line = 0;
for (j = 1; j <= 8; j++)
{
cout << chess[i][j];
line++;
}
if (line == 8)
cout << endl;
}
}
int main (void)
{
int T;
cin >> T;
while (T--)
{
memset(chess, '\0', sizeof(chess));
int i, j;
string s;
for (i = 1; i <= 8; i++)
{
cin >> s;
for (j = 0; j < s.size(); j++)
chess[i][j+1] = s[j];
}
char player;
while (cin >> player)
{
string order;
while (cin >> order)
{
if (order[0] == 'L')
L(player);
else if (order[0] == 'M')
{
int r, c;
r = order[1]-'0';
c = order[2]-'0';
M(player, r, c);
}
else if (order[0] == 'Q')
{
Q();
break;
}
else
break;
}
break;
}
}
return 0;
}