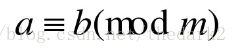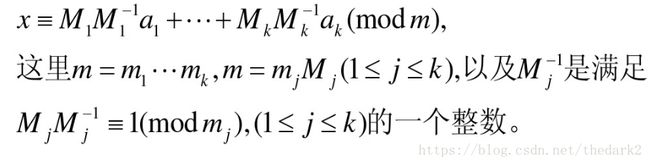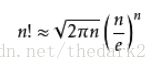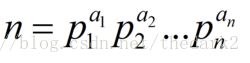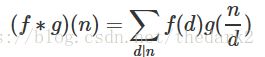数论知识点总结
算数基本定理(唯一分解定理)
任何一个大于1的自然数![]() ,都可以唯一分解成有限个质数的乘积
,都可以唯一分解成有限个质数的乘积 ![]()
,这里 ![]() 均为质数,其诸指数
均为质数,其诸指数 ![]() 是正整数。
是正整数。
这样的分解称为 ![]() 的标准分解式。
的标准分解式。
费马小定理
假如p是质数,且gcd(a,p)=1,那么![]()
实际上,它是欧拉定理的一个特殊情况
即
卡迈克尔数
卡迈克尔数的定义是对于合数n,如果对于所有正整数b,b和n互素,都有同余式 ![]() 成立,则合数n为Carmichael数
成立,则合数n为Carmichael数
素数和合数
素数分布的规律:自然数增加1倍后,素数增长趋势是:逐渐也增加1倍。1e7->173756个 极限 1e6->2e4左右
O(N)素数筛法:一个合数可以表示成若干个素数的积
比如说 i = 6 =2 * 3 , A = p1 * p2 * p3 .. * pn , 其中pi为素数 ,p1最小 ,只筛到p1 * i即可
我们只筛 最小的 2 * i 不筛3 * i ;
for(int i=2;i素数的判断:
常规素数判断O(sqrt(n)3)
int isPrime(int n)
{ //返回1表示判断为质数,0为非质数,在此没有进行输入异常检测
float n_sqrt;
if(n==2 || n==3) return 1;
if(n%6!=1 && n%6!=5) return 0;
n_sqrt=floor(sqrt((float)n));
for(int i=5;i<=n_sqrt;i+=6)
{
if(n%(i)==0 | n%(i+2)==0) return 0;
}
return 1;
} Miller-Rabin算法
速度快,而且可以判断 <2^63的数
const int S=20;//随机算法判定次数,S越大,判错概率越小
//计算 (a*b)%c. a,b都是long long的数,直接相乘可能溢出的
// a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
a%=c;
b%=c;
long long ret=0;
while(b)
{
if(b&1){ret+=a;ret%=c;}
a<<=1;
if(a>=c)a%=c;
b>>=1;
}
return ret;
}
//计算 x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
if(n==1)return x%mod;
x%=mod;
long long tmp=x;
long long ret=1;
while(n)
{
if(n&1) ret=mult_mod(ret,tmp,mod);
tmp=mult_mod(tmp,tmp,mod);
n>>=1;
}
return ret;
}
//以a为基,n-1=x*2^t a^(n-1)=1(mod n) 验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
long long ret=pow_mod(a,x,n);
long long last=ret;
for(int i=1;i<=t;i++)
{
ret=mult_mod(ret,ret,n);
if(ret==1&&last!=1&&last!=n-1) return true;//合数
last=ret;
}
if(ret!=1) return true;
return false;
}
// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数,但概率极小)
//合数返回false;
bool Robin_Miller(long long n)
{
if(n<2)return false;
if(n==2)return true;
if((n&1)==0) return false;//偶数
long long x=n-1;
long long t=0;
while((x&1)==0){x>>=1;t++;}
for(int i=0;i分解因子:Pollard_rho 算法
int pollard_rho(int n, int c)///c为自己设定的某值
{
int x, y, d, i = 1, k = 2;
x = rand() % (n - 1) + 1;
y = x;
while (true)
{
++i;
x = (modular_multi(x, x, n) + c) % n;
d = gcd(y - x, n);
if (1 < d && d < n)
return d;
if (x == y)
return n;
if (i == k)
y = x, k <<= 1;
}
}容斥原理
定义:如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。(A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C)
![]()
![]()
同余
设m!=0,若m|a-b,即a-b=km,则称b同余于b模m记为
实际也就是a%m=b
同余的性质
若m>=1,gcd(a,m)=1,则存在c使得ca同余于1mod m
我们把c称为a对模m的逆(元),记做
逆元的求法
- 欧拉定理
- 费马小定理(欧拉定理的特殊情况)
- Exgcd(gcd(a,MOD)=1)
模运算
a%c+b%c=(a+b)%c //减法同样适用
a%c*b%c=a*b%c
a/b%c=a*inv(b)%c
中国剩余定理
设m1…mk是两两互素的正整数,那么对任意整数a1…ak
一次同余方程组x%mj=aj 1<=j<=k必有解且解数是1事实上这个同余方程组的解是
除法定理和余数
除法定理:对于任意整数a和任意整数n,存在唯一的整数q和r,使得a=qn+r,其中0<= r< n。
值q称为除法的商,值r=a (mod n)称为除法的余数
公约数与最大公约数
d是a的约数并且也是b的约数,则d是a和b的公约数。
两个不同时为0整数a和b的最大公约数表示为gcd(a,b)
欧几里得算法
定理:gcd(a,b) = gcd(b,a mod b)
证明: a可以表示成a = kb + r,则r = a mod b
1.假设d是a,b的一个公约数,则有
a|d, b|d,而r = a - kb,因此r|d
因此d是(b,a mod b)的公约数,证明充分性
2.假设d 是(b,a mod b)的公约数,则
b|d , r|d ,但是a = kb +r
因此d也是(a,b)的公约数,证明必要性
因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等。
当b=0时,(a,0)的最大公约数是a
gcd(a,b)的性质
定理: 如果a,b时不全为0的任意整数,则gcd(a,b)是a与b的线性组合ax+by的最小正元素即ax+by=gcd(a,b)
推论1:对于任意整数a,b ,如果d|a且d|b则d|gcd(a,b)
推论2:对于所有整数a和b以及任意非负整数n,gcd(an,bn)=n*gcd(a,b)。
推论3:对所有正整数n,a和b,如果n|ab并且gcd(a,n)=1,则n|b
拓展欧几里得算法
定理: 对于不完全为0的非负整数a,b,gcd(a,b) 表示a和b的最大公约数d,必然存在整数对x,y使得gcd(a,b)=d=ax+by。
对于gcd(a,b)=d,对(a,b)用gcd辗转相除得(d,0)。此时把a=d,b=0;带入方程显然x=1,y等于任意值由此可以得出exgcd的递归出口逆推出ax+by=d的所有解
最小公倍数LCM
LCM(a,b)=a*b/gcd(a,b)不过一般写成a/gcd(a,b)*b
关于N!:
威尔逊定理
p|(p-1)!+1 if and only if p is a prime
斯特林公式
积性函数
定义:积性函数指对于所有互质的整数a和b有性质f(ab)=f(a)f(b)的数论函数。
狄利克雷卷积
定义f,gf,g两个函数的狄利克雷卷积(∗)(∗)运算为:
欧拉函数
在数论,对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1)
其中p1, p2……pn为x的所有质因数,x是不为0的整数。
欧拉定理引理
①:如果n为某一个素数p,则φ(p)=p-1
②:如果n为某一个素数p的幂次,那么φ(p^a)=(p-1)*p^(a-1)
③:如果n为任意两个数a和b的积,那么φ(a*b)=φ(a)*φ(b)
④:设n=(p1^a1)*(p2^a2)*……*(pk^ak) (为N的分解式)
那么φ(n)=n*(1-1/p1)*(1-1/p2)*……*(1-1/pk)
欧拉定理
若n,a为正整数,且n,a互质,则:
![]()
莫比乌斯函数
莫比乌斯反演定理
设 和 是定义在正整数集合上的两个函数,定义如下。
则
自然数幂和与伯努利数 https://blog.csdn.net/whai362/article/details/43148939
拉格朗日插值法详解 https://www.cnblogs.com/ECJTUACM-873284962/p/6833391.html