MD5密码的简单分析与代码实现

MD5算法是一种Hash函数的加密算法，输入的序列长度小于2^64比特，输出的长度则为固定的128比特，是一种单向加密。是通过直接构造复制的非线性关系实现单向性。大体的流程如下图所示：

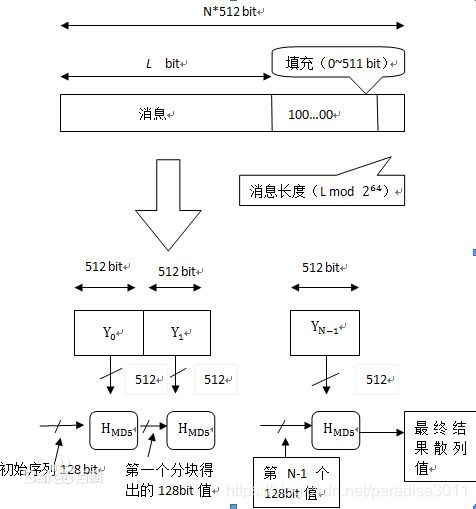
算法的具体过程如下：

1. 附加填充位

在明文（二进制序列）的后面填充一个1和若干个0使得消息的长度模512与448同余。若原来的明文长度大于模512大于448，则填充的下一个512分组。例如原来的消息长度为500，则填充之后的长度为512+448。最后的64位存放消息的长度，不够的在后面补0直到64位为止。

2. 初始化向量

MD5使用32位的寄存器A,B,C,D，最开始存放的是4个固定的值：
A=0x01234567 B=0x89ABCDEF C=0xFEDCBA98 D=0x76543210
同时，在寄存器里面其实的小端序存储，在代码中实际上我们要变换顺序，例如A=0x67452301。

3. 分组处理

分组处理包括4轮。对应上图的HMD5。明文分成若干个512比特的分组，将4个寄存器里面的值和每一个512位的分组进行迭代，最后的散列值即为最后的MD5值。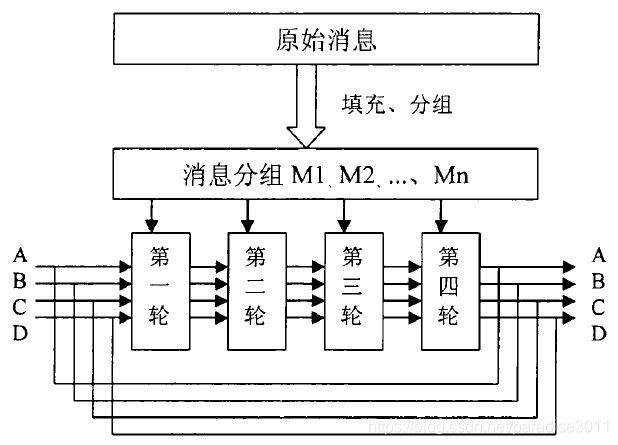
512位的分组又分解为16个32位分组，对应到每一轮的16个步函数里面，对应的索引在代码中列出。4轮结束后将得到的向量与初始的进行模2^32加。

4. 步函数

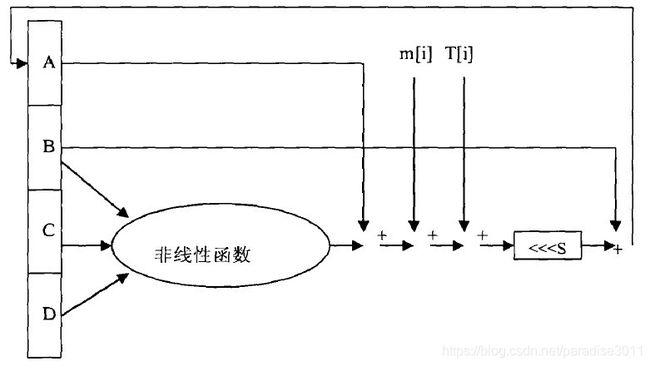
如图所示，A分别与B,C,D的非线性函数，m[i]（明文的32位分组），T[i]（伪随机常数）进行模加厚循环左移一定的位数，与B模加后赋给B，B->C，C->D，D->A。

附上MD5完整的python代码：

#coding=utf-8

str1 = "iscbupt"

AA = 0x67452301
BB = 0xefcdab89
CC = 0x98badcfe
DD = 0x10325476
#伪随机数T
T = [0xD76AA478,0xE8C7B756,0x242070DB,0xC1BDCEEE,0xF57C0FAF,0x4787C62A,0xA8304613,0xFD469501,
	 0x698098D8,0x8B44F7AF,0xFFFF5BB1,0x895CD7BE,0x6B901122,0xFD987193,0xA679438E,0x49B40821,
	 0xF61E2562,0xC040B340,0x265E5A51,0xE9B6C7AA,0xD62F105D,0x02441453,0xD8A1E681,0xE7D3FBC8,
	 0x21E1CDE6,0xC33707D6,0xF4D50D87,0x455A14ED,0xA9E3E905,0xFCEFA3F8,0x676F02D9,0x8D2A4C8A,
	 0xFFFA3942,0x8771F681,0x6D9D6122,0xFDE5380C,0xA4BEEA44,0x4BDECFA9,0xF6BB4B60,0xBEBFBC70,
	 0x289B7EC6,0xEAA127FA,0xD4EF3085,0x04881D05,0xD9D4D039,0xE6DB99E5,0x1FA27CF8,0xC4AC5665,
	 0xF4292244,0x432AFF97,0xAB9423A7,0xFC93A039,0x655B59C3,0x8F0CCC92,0xFFEFF47D,0x85845DD1,
	 0x6FA87E4F,0xFE2CE6E0,0xA3014314,0x4E0811A1,0xF7537E82,0xBD3AF235,0x2AD7D2BB,0xEB86D391]
#循环左移位数
S = [7,12,17,22,7,12,17,22,7,12,17,22,7,12,17,22,5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20,
	 4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23,6,10,15,21,6,10,15,21,6,10,15,21,6,10,15,21,]
#每一个步函数所用到的m
index = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12,
		 5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2,0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9]

def Not(m):							#比特非运算
	list_m = list(str(bin(m)[2:]).zfill(32))		#高位是0的时候容易舍去，应该补上
	for i in range(0,len(list_m)):
		list_m[i] = str((int(list_m[i])+1)%2)
	return int("".join(list_m),2)

def move(x,s):						#循环左移s位
	x = str(bin(x)[2:]).zfill(32)	#整形计算时容易将最高位0去掉，移位时应该补上
	x = x[s:]+x[:s]
	return int(x,2)

def reserve(x,n):						#小端序存储应该改变顺序
	k = ""
	for i in range(n/8,0,-1):
		k = k+x[(i-1)*8:i*8]
	return k

def fill(m):						#附加填充位
	mo = len(m)%512
	if mo!=448:
		m = m+"1"
		while len(m)%512!=448:
			m = m+"0"
	b = str(bin(len(str1)*8))[2:].zfill(64)
	b = reserve(b,64)
	m = m+b
	return m

def init_Vector(x):                #int转换成字符比特流
	x = str(bin(x)[2:]).zfill(32)
	return x

def step(a,b,c,d,r,s,m):			#步函数
	A = int(a,2)
	B = int(b,2)
	C = int(c,2)
	D = int(d,2)
	A = (A+F(B,C,D,r))&0xFFFFFFFF
	k = reserve(m,32)
	A = (A+int(k,2))&0xFFFFFFFF
	A = (A+T[r*16+s])&0xFFFFFFFF
	A = move(A,S[r*16+s])
	A = (A+B)&0xFFFFFFFF
	A,B = B,A
	A,C = C,A
	A,D = D,A
	return init_Vector(A),init_Vector(B),init_Vector(C),init_Vector(D)

def F(b,c,d,r):					#四个非线性函数
	if r==0:
		x = (b&c)|(Not(b)&d)
	if r==1:
		x = (b&d)|(c&Not(d))
	if r==2:
		x = b^c^d
	if r==3:
		x = c^(b|Not(d))
	return x

def iteration(a,b,c,d,m):		#进行64轮迭代
	A = a
	B = b
	C = c
	D = d
	M = []
	for i in range(0,16):		#m为明文分组
		M.append(m[:32])
		m = m[32:]
	for i in range(0,4):
		for j in range(0,16):
			A,B,C,D = step(A,B,C,D,i,j,M[index[i*16+j]])
	A = reserve(init_Vector((int(A,2)+int(a,2))&0xFFFFFFFF),32)
	B = reserve(init_Vector((int(B,2)+int(b,2))&0xFFFFFFFF),32)
	C = reserve(init_Vector((int(C,2)+int(c,2))&0xFFFFFFFF),32)
	D = reserve(init_Vector((int(D,2)+int(d,2))&0xFFFFFFFF),32)
	return A,B,C,D

def Encrypt(m):
	m = fill(m)
	a = init_Vector(AA)
	b = init_Vector(BB)
	c = init_Vector(CC)
	d = init_Vector(DD)
	for i in range(0,len(m)/512):
		a,b,c,d = iteration(a,b,c,d,m)
	print hex(int(a,2))[2:]+hex(int(b,2))[2:]+hex(int(c,2))[2:]+hex(int(d,2))[2:]
	
if __name__ == '__main__':
	m =""
	for i in str1:
		m += str(bin(ord(i))[2:]).zfill(8)
	Encrypt(m)