洛谷图基础，最短路与连通性

P1363 幻想迷宫

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1505;
bool a[MAXN][MAXN];
int visit[MAXN][MAXN][3];
int f[4][2] = {
      {
     1,0},{
     -1,0},{
     0,1},{
     0,-1} };
int n, m;
int bx, by;
bool f1;
//看了题解才弄出来的，这题恶心的点有几个
//1个是如何避免弄到父节点（即上一个递归过来的点），如果用visit判断，那不行，因为我们判断能无限是得基于visit为true得基础上，所以好方法就是对于visit开3为，0记录是否访问，1和2记录访问得点得x，y坐标
void dfs(int x, int y,int lx,int ly) {
     
	if (f1)return;
	//如果访问过了，并且第一次记录的坐标与这一次不重复
	if (visit[x][y][0] && (visit[x][y][1] != lx || visit[x][y][2] != ly)) {
     
		f1 = 1;
		return;
	}
	//对于图x,y点，第一次记录坐标为lx，ly
	visit[x][y][0] = 1, visit[x][y][1] = lx, visit[x][y][2] = ly;
	for (int i = 0;i < 4;i++) {
     
		int xx = (x + f[i][0] + n) % n, yy = (y + f[i][1] + m) % m;
		int lxx = lx + f[i][0], lyy = ly + f[i][1];
		//如果可以访问
		if (!a[xx][yy]) {
     
		//这个判断对我来说是难点，首先前2个判断是否是访问过的点（即访问后的点或是否是父节点）后面一个判断如果点是（0，0）或者（n，m）
			if (visit[xx][yy][1] != lxx || visit[xx][yy][2] != lyy || !visit[xx][yy][0])
				dfs(xx, yy, lxx, lyy);
		}
	}
}
int main() {
     
	ios::sync_with_stdio(false);
	while (cin >> n >> m) {
     
		f1 = 0;
		memset(a, 0, sizeof(a));
		memset(visit, 0, sizeof visit);
		for (int i = 0;i < n;i++) {
     
			for (int j = 0;j < m;j++) {
     
				char ch;
				cin >> ch;
				if (ch == '#')a[i][j] = 1;
				if (ch == 'S')bx = i, by = j;
			}
		}
		dfs(bx, by, bx, by);
		if (f1)cout << "Yes" << endl;
		else cout << "No" << endl;
	}
}

P1127 词链

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1005;
int n;
string s[MAXN];
int out[26], in[26];
int p=-1, q=-1;
vector<string>ans;
string res;
bool flag = false;
vector<string>edge[26];
map<string, int>m;
//cmp用来找字典序最小的
bool cmp(string a, string b) {
     
	return a < b;
}
//这种题其实找连通路
void dfs(int f,int num) {
     
//如果找到了答案
	if (num == n) {
     
		int si = ans.size();
		for (int i = 0;i < si;i++) {
     
			res += ans[i];
			res += '.';
		}
		res.pop_back();
		flag = true;
		return;
	}
	//按字典序排序
	sort(edge[f].begin(), edge[f].end(),cmp);
	int sii = edge[f].size();
	for (int i = 0;i <sii;i++) {
     
	//寻找可以使用的边（单词）
		if (m[edge[f][i]] > 0) {
     
			m[edge[f][i]]--;
			ans .push_back( edge[f][i]);//可以的单词入ans
			int len = edge[f][i].length();
			dfs(edge[f][i][len - 1] - 'a', num + 1);//继续dfs，如果最后可以，flag=true
			if (flag == false){
     //如果最后不能成为词链
				ans.pop_back();
				m[edge[f][i]]++;//回溯
			}
			else return;//找到了直接return，加快程序
		}
	}
}

int main() {
     
	cin >> n;
	for (int i = 1;i <= n;i++) {
     
	//初始化所有数据
		cin >> s[i];
		m[s[i]]++;//记录一个单词有几个
		int len = s[i].length();
		int last = s[i][len - 1] - 'a';
		int begin = s[i][0] - 'a';
		in[last]++;
		out[begin]++;
		edge[begin].push_back(s[i]);//构成图，起点为第一个字母，终点是最后一个字母
	}
	int num = 0;
	for (int i = 0;i < 26;i++) {
     
		if (in[i] != out[i]) {
     //遇到出入度不同num++
			num++;
			if (in[i] - out[i] == 1)q = i;
			if (in[i] - out[i] == -1)p = i;
		}
	}
	if (num != 0 && num != 2) {
     
		cout << "***" << endl;//连通只有num为0和2的回路和通路2种情况

	}
	else if (num == 0) {
     //回路
		int fir = 0;
		while (in[fir] == 0)fir++;//找字典序最小的起始点
		dfs(fir, 0);
		if (res != "")cout << res << endl;
		else cout << "***" << endl;//假如基图不连通，res为空，输出***
	}
	else if (num==2&&p != -1 && q != -1) {
     
		dfs(p, 0);
		if (res != "")cout << res << endl;
		else cout << "***" << endl;//假如基图不连通，res为空，输出***
	}
	else cout << "***" << endl;//num==2,p和q有个是-1，我也不知道有没有这种可能，但是加了复杂度没啥变化
}

P1629 邮递员送信

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e3+5;
const int INF = 1e9 + 7;
int n, m;
int dis[MAXN];
bool ans[MAXN];
struct node {
     
	int x, dis_x;
	bool operator <(const node& b) const{
     
		return dis_x>b.dis_x;
	}
};
struct Edge {
     
	int x, y, w;
};
//0记录正向图，1记录反向图
//1到所有点最短距离为正向图1到所有点最短距离
//所有点到1最短距离为反向图1到所有点最短距离
vector<Edge>edge[MAXN][2];
int dj(int t) {
     
	for (int i = 1;i <= n;i++) {
     
		dis[i] = INF;
	}
	memset(ans, 0, sizeof ans);//上面是初始化，ans表示是否确定是最短路
	//下面是迪杰斯特拉算法
	priority_queue<node>q;
	dis[1] = 0;
	q.push({
      1,0 });
	while (!q.empty()) {
     
		node now = q.top();
		q.pop();
		if (ans[now.x])continue;
		ans[now.x] = true;
		for (int i = 0;i < edge[now.x][t].size();i++) {
     
			Edge e = edge[now.x][t][i];
			if (ans[e.y])continue;
			if (dis[e.y] > dis[e.x] + e.w) {
     
				dis[e.y] = dis[e.x] + e.w;
				q.push({
     e.y,dis[e.y]});
			}
			
		}
	}
	//顺便把路径和求一下
	int res = 0;
	for (int i = 1;i <= n;i++) {
     
		res += dis[i];
	}
	return res;
}

int main() {
     
	ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		int from, to, w;
		cin >> from >> to >> w;
		edge[from][0].push_back({
      from,to,w });
		edge[to][1].push_back({
      to,from,w });//存反向边
	}
	int res = 0;
	res += dj(0);//求正向路
	res += dj(1);//求反向路
	cout << res << endl;

}

P1144 最短路计数

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e6+5;
const int INF = 1e9 + 7;
const int mod = 100003;
int n, m;
int dis[MAXN];
int ans[MAXN];
bool vis[MAXN];
vector<int>edge[MAXN];
void bfs() {
     
	queue<int>q;
	q.push(1);
	dis[1] = 0;
	ans[1] = 1;
	vis[1] = 1;
	while (!q.empty()) {
     
		int f = q.front();
		q.pop();
		for (int i = 0;i < edge[f].size();i++) {
     
			int now = edge[f][i];
			//如果这个点是第一次访问，由于边权值为1，bfs肯定访问到最短路，所以更新dis和vis
			if (!vis[now]) {
     
				vis[now] = 1;
				dis[now] = dis[f]+1;
				q.push(now);
			}
			//对于所有再次遍历到now的点，观察其当前父节点的dis，所以等式不等于，说明f父亲结点并不是连向
			if (dis[now] == dis[f] + 1)ans[now] = (ans[now] + ans[f]) % mod;
		}
	}
}
int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		int a, b;
		cin >> a >> b;
		edge[a].push_back(b);
		edge[b].push_back(a);
	}
	bfs();
	for (int i = 1;i <= n;i++) {
     
		cout << ans[i]%mod << endl;
	}
	return 0;
}

P1462 通往奥格瑞玛的道路

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e4+5;
const int INF = 2e9 + 7;
const int mod = 100003;
int n, m, b;
int dis[MAXN];
bool vis[MAXN];
struct Node {
     
	int x, f,dis_x;
	bool operator < (const Node& a)const {
     
		return dis_x > a.dis_x;
	}
}node[MAXN];
struct Edge {
     
	int from, to, c;
};//迪杰斯特拉算法建立边与点
vector<Edge>edge[5 * MAXN];
bool dj(int mf) {
     
	memset(vis, 0, sizeof vis);
	for (int i = 1;i <= n;i++)dis[i] = INF;//初始化
	priority_queue<Node>q;
	if (node[1].f > mf)return false;//二分费用，mf是二分到的，我们走的城市不能超过mf
	q.push({
      node[1].x,node[1].f,0 });
	dis[1] = 0;
	while (!q.empty()) {
     
		Node now = q.top();
		q.pop();
		if (vis[now.x])continue;
		if (now.dis_x > b)return false;//这算法每次都会得到一个点的最短路，如果最短都超过了b，那么肯定不行
		vis[now.x] = true;
		if (now.x == n)return true;//如果到了n就可以返回了true，因为我们这算法判断最大费用mf时是否可以到n
		for (int i = 0;i < edge[now.x].size();i++) {
     
			Edge p = edge[now.x][i];
			if (node[p.to].f > mf) {
      vis[p.to] = true;continue; }//用vis，防止一些多余操作
			if (vis[p.to])continue;
			if (dis[p.to] > dis[now.x] + p.c) {
     
				dis[p.to] = dis[now.x] + p.c;
				q.push({
      p.to,node[p.to].f,dis[p.to] });
			}
		}
	}
	//下面3行加不加无所谓，只是为了更直观的判断，因为dis<=b肯定的，不然会在循环中弄掉，
	if (dis[n] <= b)
		return true;
	else return false;
}
int main() {
     
	cin >> n >> m >> b;
	int maxf = 0;
	for (int i = 1;i <= n;i++) {
     
		cin >> node[i].f;
		node[i].x = i, node[i].dis_x = INF;
		if (node[i].f > maxf)maxf = node[i].f;
	}
	for (int i = 1;i <= m;i++) {
     
		int a, b, c;
		cin >> a >> b >> c;
		edge[a].push_back({
      a,b,c });
		edge[b].push_back({
      b,a,c });
	}
	int l = 1,r = maxf;
	if (!dj(maxf)) {
      cout << "AFK" << endl; }
	else {
     
		while (l < r) {
     //看到最大值中的最小值问题几乎都是二分
			int mid = (l + r) / 2;
			if (dj(mid))r = mid;
			else l = mid + 1;
		}
		cout << l << endl;
	}
}

P3387【模板】缩点

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e4+5;
const int INF = 2e9 + 7;
const int mod = 100003;
int n, m;
int w[MAXN];
int num[MAXN], low[MAXN];
int scc[MAXN],ans[MAXN];
int in[MAXN];
int dfn =0,cnt= 0;
stack<int>st;
vector<int>edge[MAXN];
//这题和hdu1827很像，都是缩点+拓扑，建议读者先看一题再练一题
//dfs求缩点
void dfs(int u) {
     
	low[u] = num[u] = ++dfn;
	st.push(u);
	for (int i = 0;i < edge[u].size();i++) {
     
		int v = edge[u][i];
		//这边不是割点割边的知识，所以不用判断是不是父节点，哪怕是，也会再else'if那把low值更新成一样，方便缩点
		if (num[v] == 0) {
     
			dfs(v);
			low[u] = min(low[v], low[u]);
		}
		else if (scc[v] == 0)low[u] = min(low[u], num[v]);
	}
	if (low[u] == num[u]) {
     //一旦到这，所有的一个环的点都在st中
		cnt++;//标记环，进行缩点
		int now;
		do {
     
			now = st.top();
			st.pop();
			scc[now] = cnt;
			ans[cnt] += w[now];
		} while (now != u);
	}
}
vector<int>e[MAXN];
int res[MAXN];
int topo() {
     

	queue<int>q;
	for (int i = 1;i <= cnt;i++) {
     
		if (in[i] == 0) {
      q.push(i); res[i] = ans[i]; }
	}
	int maxn = 0;
	while (!q.empty()) {
     
		int now = q.front();
		q.pop();
		for (int i = 0;i < e[now].size();i++) {
     
			int v = e[now][i];
			in[v]--;
			//拓扑+dp
			res[v] = max(res[v], res[now] + ans[v]);
			if (in[v] == 0) {
     
				q.push(v);
			}
		}
	}
	for (int i = 1;i <= cnt;i++) {
     
		if (maxn < res[i])maxn = res[i];
	}
	return maxn;
}
	int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= n;i++)cin >> w[i];
	for (int i = 1;i <= m;i++) {
     
		int from, to;
		cin >> from >> to;
		edge[from].push_back(to);
	}
	for (int i = 1;i <= n;i++) {
     
		if (!num[i])dfs(i);
	}
	//建立缩点后的边
	for (int i = 1;i <=n;i++){
     
		for (int j = 0;j < edge[i].size();j++) {
     
			int p = edge[i][j];
			if (scc[i] == scc[p])continue;
			in[scc[p]]++;
			e[scc[i]].push_back(scc[p]);
		}
	}
	
	cout << topo() << endl;
}

P2341 【USACO03FALL】【HAOI2006】受欢迎的牛 G

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e4+5;
const int INF = 2e9 + 7;
const int mod = 100003;
int n, m;
int w[MAXN];
int num[MAXN], low[MAXN];
int scc[MAXN],ans[MAXN];
int in[MAXN],out[MAXN];
int dfn =0,cnt= 0;
stack<int>st;
vector<int>edge[MAXN];
vector<int>e[MAXN];
int pp;
//其实只要知道这题的核心就不难，这题就是找缩点后出度为0的点，如果有多个，那么不可能

void dfs(int u) {
     //日常tarjan
	num[u] = low[u] = ++dfn;
	st.push(u);
	for (int i = 0;i < edge[u].size();i++) {
     
		int v = edge[u][i];
		if (!num[v]) {
     
			dfs(v);
			low[u] = min(low[v], low[u]);
		}
		else if (scc[i] == 0) {
     
			low[u] = min(low[u], num[v]);
		}
	}
	if (low[u] == num[u]) {
     
		int now;
		cnt++;
		do {
     
			now = st.top();
			st.pop();
			scc[now] = cnt;
			ans[cnt]++;
		} while (now != u);
	}
}
void solve() {
     
	int ff = 0;
	for (int i = 1;i <= cnt;i++) {
     
		if (out[i] == 0) {
     
			if (ff) {
     
				cout << 0 << endl;
				return;
			}
			ff = i;
		}
	}
	cout << ans[ff] << endl;
}
int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		int from, to;
		cin >> from >> to;
		edge[from].push_back(to);
	}
	for (int i = 1;i <= n;i++) {
     
		if (!num[i]) {
     dfs(i); }//这里不用判断有几个图，毕竟有向图判断有几个图比较难，后面solve会删选情况
	}
	for (int i = 1;i <= n;i++) {
     
		for (int j = 0;j < edge[i].size();j++) {
     
			int v = edge[i][j];
			if (scc[i] == scc[v])continue;
			out[scc[i]]++;
		}
	}
	solve();
}

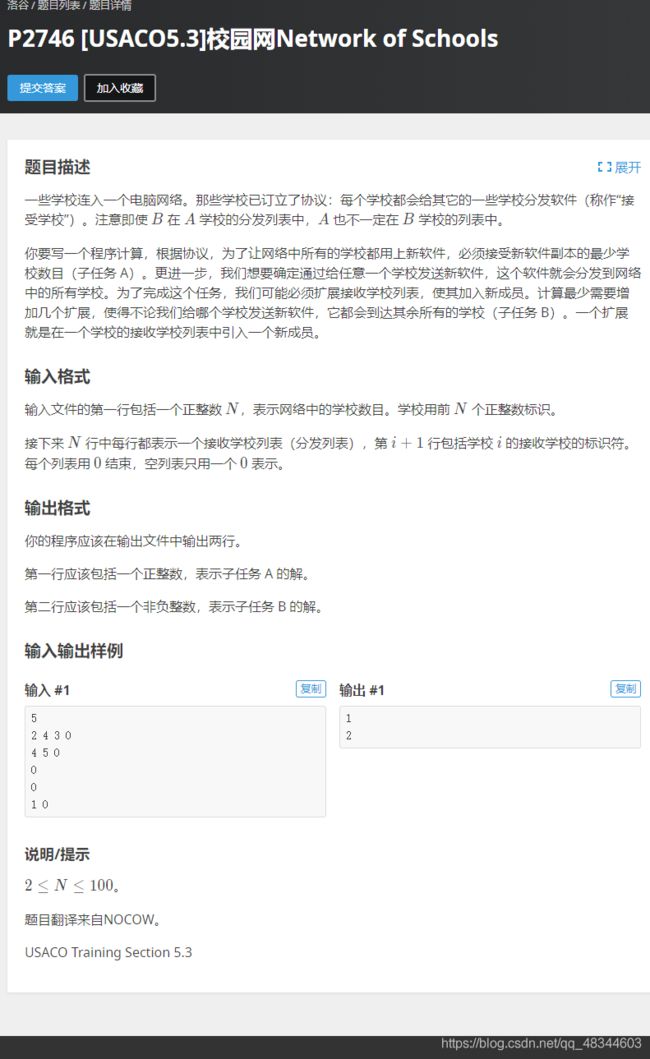
P2746 [USACO5.3]校园网Network of Schools

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e4+5;
const int INF = 2e9 + 7;
const int mod = 100003;
int n;
int w[MAXN];
int num[MAXN], low[MAXN];
int scc[MAXN],ans[MAXN];
int in[MAXN],out[MAXN];
int dfn =0,cnt= 0;
stack<int>st;
vector<int>edge[MAXN];
vector<int>e[MAXN];
int pp;
//tarjan+缩点
void dfs(int u) {
     
	low[u] = num[u] = ++dfn;
	st.push(u);
	for (int i = 0;i < edge[u].size();i++) {
     
		int v = edge[u][i];
		if (num[v] == 0) {
     
			dfs(v);
			low[u] = min(low[v], low[u]);
		}
		else if (scc[v] == 0) {
     
			low[u] = min(low[u], num[v]);
		}
	}
	if (low[u] == num[u]) {
     
		int now;
		cnt++;
		do {
     
			now = st.top();
			st.pop();
			scc[now] = cnt;
		} while (now != u);
	}
}
int res1, res2;
//第一问就是求有个入度为0的点
//第二问就是给你个有向图，问加几条边可以使他强连通

void solve() {
     
	for (int i = 1;i <= cnt;i++) {
     
		if (in[i] == 0)res1++;//第一问直接统计
		if (out[i] == 0)res2++;//第二问比较图出度为0与入度为0的点的较大值
		
	}
	res2 = max(res2, res1);
	if (cnt == 1)res2 = 0;//如果缩点缩成一个点，那么就要特判
	cout << res1 << endl;
	cout << res2 << endl;
}
int main() {
     
	cin >> n;
	for (int i = 1;i <= n;i++) {
     
		int to;
		cin >> to;
		while (to != 0) {
     
			edge[i].push_back(to);
			cin >> to;
		}
	}
	for (int i = 1;i <= n;i++) {
     
		if (!num[i])dfs(i);
	}
	for (int i = 1;i <= n;i++) {
     
		for (int j = 0;j < edge[i].size();j++) {
     
			int v = edge[i][j];
			if (scc[v] == scc[i])continue;
			in[scc[v]]++, out[scc[i]]++;
		}
	}
	solve();
}

P2047 [NOI2007]社交网络

//点少，所以floyed，其次floye途中顺便把2点之间的最短路条数弄出
//对于过了v的最短路条数，假设起始点是i，终点为j，当一个i到v的距离+v到j的距离等于i到j 的距离时，v就是再最短路上，那么这个条数就等于i到v最短路的条数*v到j的最短路条数
//同时我们不能让i，j，v互相相等，因为题目写了s！=v啥的
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 105;
int mp[MAXN][MAXN];
ll num[MAXN][MAXN];
double ans[MAXN] = {
      0 };
int n, m;
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 1;i < MAXN;i++) {
     
		for (int j = 1;j < MAXN;j++) {
     
			mp[i][j] = 999999999;
		}
	}
	for (int i = 1;i <= m;i++) {
     
		int a, b, w;
		cin >> a >> b >> w;
		mp[a][b] = w;
		mp[b][a] = w;
		num[a][b] = num[b][a] = 1;//记得最短路条数初始化
	}
	for (int k = 1;k <= n;k++) {
     
		for (int i = 1;i <= n;i++) {
     
			for (int j = 1;j <= n;j++) {
     
				if (mp[i][j] > mp[i][k] + mp[k][j]) {
     
					mp[i][j] = mp[i][k] + mp[k][j];
					num[i][j] = num[i][k] * num[k][j];//若不初始化，则num一直是0
				}
				else if (mp[i][j] == mp[i][k] + mp[k][j]) {
     
					num[i][j]+= num[i][k] * num[k][j];
				}
			}
		}
	}
	for (int k = 1;k <= n;k++) {
     
		for (int i = 1;i <= n;i++) {
     
			for (int j = 1;j <= n;j++) {
     
				if (k == i || k == j || i == j)continue;
				if (mp[i][k] + mp[k][j] == mp[i][j]) {
     
					ans[k] += 1.0 * num[i][k] * num[k][j] / num[i][j];
				}
			}
		}
	}
	for (int i = 1;i <= n;i++) {
     
		cout << fixed << setprecision(3) << ans[i] << endl;
	}
	return 0;
}

P2966 [USACO09DEC]Cow Toll Paths G

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 255;
int mp[MAXN][MAXN];
int dis[MAXN][MAXN];
int val[MAXN];
int md[MAXN][MAXN];
int ran[MAXN];
int n, m,p;
struct Node {
     
	int id, val;
	bool operator<(const Node& a) const{
     
		return val < a.val;
	}
};//按点权排序
Node node[MAXN];
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m >> p;

	for (int i = 1;i <= n;i++) {
      cin >> node[i].val; node[i].id = i; }
	sort(node + 1, node + n + 1);
	for (int i = 1;i <= n;i++) {
     
		ran[node[i].id] = i;//排完序后将每个点的id改为我们按点权拍完的id
	}
	memset(mp, 0x3f, sizeof mp);
	for (int i = 1;i <= n;i++)mp[i][i] = 0;
	for (int i = 1;i <= m;i++) {
     
		int a, b, w;
		cin >> a >> b >> w;
		mp[ran[a]][ran[b]] = mp[ran[b]][ran[a]] = min(mp[ran[a]][ran[b]],w);//防止重边
	}
	memset(dis, 0x3f, sizeof dis);
	for (int k = 1;k <= n;k++) {
     
		for (int i = 1;i <= n;i++) {
     
			for (int j = 1;j <= n;j++) {
     
				if (i == j)continue;
				if (mp[i][j] > mp[i][k] + mp[k][j]) {
     
					mp[i][j] = mp[i][k] + mp[k][j];//因为我们是按点权排序的，所以在k不断递增过程中，后面的mp[i][j]只能通过这步然后加上点权更新，如果这个没更新，那么后面的dis肯定不会更新，（但是在初始状态每个dis都是很大时会更新）
				}
				int maxn = max(node[k].val, max(node[i].val, node[j].val));
				dis[i][j] = min(dis[i][j], mp[i][j] + maxn);
			}
		}
	}
	for (int i = 1;i <= p;i++) {
     
		int s,t;
		cin >> s >> t;
		cout << dis[ran[s]][ran[t]] << endl;
	}
	return 0;
}

P3379 【模板】最近公共祖先（LCA）

//0.我们得预处理各个点得深度，即dep数组，初始化倍增的点，即nex数组
//1.对于给定的2个点，我们让dep大的点往上移动，与另一个点保持dep相同
//2.dep保持相同时，判断两点是否重合，重合则为公共点
//3.不重合，同时向上移动，移动到最后一个不重叠的点（再向上就会重叠）
//4.得到最后一个不重叠的点，再往上移动一位
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 5e5 + 5;
int n, m,s;
vector<int>edge[MAXN];
int dep[MAXN];
int nex[MAXN][21];
void dfs( int x,int fa) {
     
	dep[x] =dep[fa]+1 ;
	nex[x][0] = fa;
	for (int i = 1;(1 << i) <= dep[x];i++) {
     
		nex[x][i] = nex[nex[x][i - 1]][i - 1];
	}
	for (int i = 0;i < edge[x].size();i++) {
     
		int v = edge[x][i];
		if (v!=fa) {
     
			dfs(v,x);
		}
	}
}//dfs为步骤0，预处理
int lca(int a, int b) {
     
	if (dep[a] < dep[b])swap(a, b);
	for (int i = 20;i >= 0;i--) {
     
		if (dep[a] - (1 << i) >= dep[b])a = nex[a][i];
	}//步骤1
	if (a == b)return a;//步骤2
	for (int i = 20;i >= 0;i--) {
     
		if (nex[a][i] != nex[b][i]) {
     
			a = nex[a][i], b = nex[b][i];
		}
	}//步骤3
	return nex[a][0];//步骤4
}
int main(){
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m >> s;
	for (int i = 1;i <= n-1;i++) {
     
		int a, b;
		cin >> a >> b;
		edge[a].push_back(b);
		edge[b].push_back(a);
	}
	dfs( s,0);
	for (int i = 1;i <= m;i++) {
     
		int a, b;
		cin >> a >> b;
		cout << lca(a, b) << endl;
	}
}

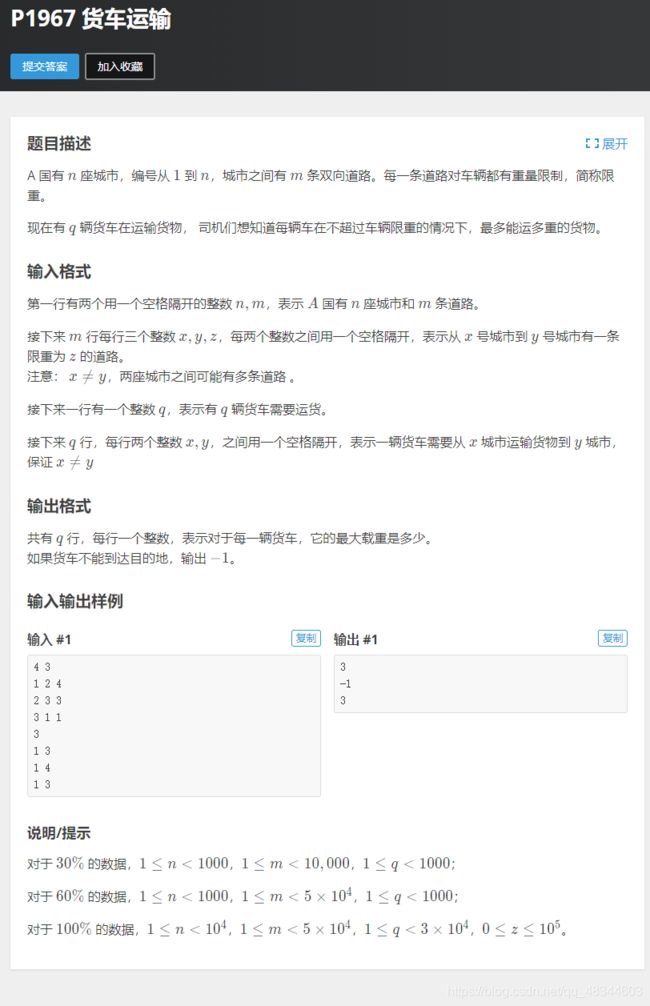
P1967 货车运输

//恶心的一批的一题，主要是我LCA刚学，对LCA倍增维护值不熟悉，折磨我一上午
//1.存图，得到最大生成树，并查集，图论建边
//2.dfs得到深度以及预处理
//3.维护f与w数组值
//4.lca
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e4 + 5;
int n, m, t;
int fa[MAXN];
int f[MAXN][21];
int d[MAXN];
int w[MAXN][21];
bool vis[MAXN];
int findf(int x) {
     
	if (x != fa[x]) fa[x] = findf(fa[x]);
	return fa[x];
}//步骤1并查集
struct Edge {
     
	int from, to, w;
	bool operator<(const Edge& a)const {
     
		return w > a.w;
	}
};//步骤一建图
const int MAXM = 5e4 + 5;
Edge e[MAXM];
vector<Edge>edge[MAXN];
void dfs(int x) {
     
	vis[x] = true;
	for (int i = 0;i < edge[x].size();i++) {
     
		int v = edge[x][i].to;
		if (vis[v])continue;
		w[v][0] =edge[x][i].w;//边权化作点权
		d[v] = d[x] + 1;//深度加一
		f[v][0] = x;//父节点
		dfs(v);
	}
}//步骤2预处理各个点的初始值
int lca(int a, int b) {
     
	int ans = 999999999;
	if (d[a] < d[b])swap(a, b);
	for (int i = 20;i >= 0;i--) {
     
		if (d[a] - (1 << i) >= d[b]) {
     
			ans = min(w[a][i], ans);
			a = f[a][i];
		}
	}
	if (a == b)return ans;
	for (int i = 20;i >= 0;i--) {
     
		if (f[a][i] != f[b][i]) {
     
			ans = min(ans, min(w[a][i], w[b][i]));
			a = f[a][i];
			b = f[b][i];
		}
	}
	ans = min(ans, min(w[a][0], w[b][0]));
	return ans;
}//步骤4，在倍增lca中得到值
int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		cin >> e[i].from >> e[i].to >> e[i].w;
	}
	sort(e + 1, e + 1 + m);
	for (int i = 1;i <= n;i++) {
      fa[i] = i;}
	for (int i = 1;i <= m;i++) {
     
		int f1 = findf(e[i].from);
		int f2 = findf(e[i].to);
		if (f1 == f2)continue;
		else {
     
			fa[f1] = f2;
			edge[e[i].from].push_back({
      e[i].from,e[i].to,e[i].w });
			edge[e[i].to].push_back({
      e[i].to,e[i].from,e[i].w });
		}
	}//生成树
	for (int i = 1;i <= n;i++) {
     
		if (!vis[i]) {
     
			d[i] = 1;
			dfs(i);
			w[i][0] = 999999999;
			f[i][0] = i;
		}
	}//对所有点存在的边就行预处理
	for (int i = 1;i <= 20;i++) {
     
		for (int j = 1;j <= n;j++) {
     
			f[j][i] = f[f[j][i - 1]][i - 1];//这个就是j^i=j^(i/2)*j^(i/2)
			w[j][i] = min(w[j][i - 1], w[f[j][i - 1]][i - 1]);//这个意思是min[j,j+2^i]=min(min[j,(j+2^1)/2],min[(j+2^1)/2,j+2^i]
		}
	}//步骤3
	int q;
	cin >> q;
	for (int i = 1;i <= q;i++) {
     
		int from, to;
		cin >> from >> to;
		if (findf(from)!= findf(to)) {
     
			cout << -1 << endl;
			continue;//如果没连通，就输出-1
		}
		else cout << lca(from, to) << endl;
	}
}

P1991 无线通讯网

//最小生成树，得到的最大的几个边可以用那个卫星
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e3 + 5;
int n, m, t;
int fa[MAXN];
int f[MAXN][21];
int d[MAXN];
int w[MAXN][21];
bool vis[MAXN];
int findf(int x) {
     
	if (x != fa[x]) fa[x] = findf(fa[x]);
	return fa[x];
}//最小生成树，并查集
struct Node {
     
	int x,y,id;
}node[MAXN];
struct Edge {
     
	Node a, b;
	double dis;
	bool operator<(const Edge& x) {
     
		return dis < x.dis;
	}//生成树排序
};
vector<Edge>e;
vector<Edge>edge;
double getdis(Node a, Node b) {
     
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}//得到距离
int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		cin >> node[i].x >> node[i].y;
		node[i].id = i;
	}
	for (int i = 1;i <= m;i++) {
     
		for (int j = 1;j <= m;j++) {
     
			if (i == j)continue;
			e.push_back({
      node[i],node[j],getdis(node[i],node[j]) });
		}
	}
	sort(e.begin(), e.end());
	int sz = e.size();
	for (int i = 1;i <= m;i++)fa[i] = i;
	for (int i = 0;i < sz;i++) {
     
		Edge now = e[i];
		int a = now.a.id;
		int b = now.b.id;
		double dis = now.dis;
		int z1 = findf(a), z2 = findf(b);
		if (z1 == z2)continue;
		fa[z1] = z2;
		edge.push_back({
      node[a],node[b],dis });
	}
	sort(edge.begin(), edge.end());
	int len = edge.size();
	if (n == 1) {
     
		cout << fixed << setprecision(2)<< edge[len - 1].dis << endl;
	}
	else {
     
		double minn = edge[len - 1-(n-1)].dis;
		cout <<fixed<<setprecision(2)<< minn << endl;
	}
}

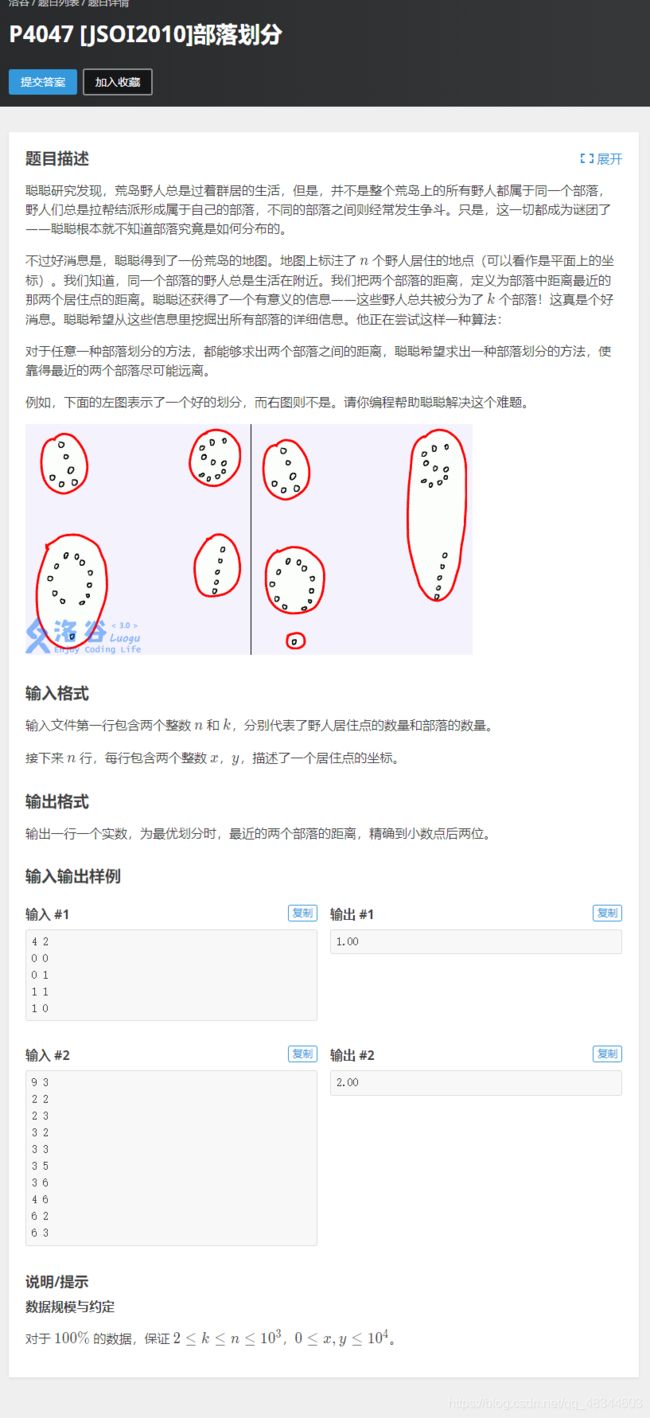
P4047 [JSOI2010]部落划分

//这题难在了思路，答案就是和上一题的一样
//为何是最小生成树，因为假设2个最近部落的最远距离是x，那么表示部落里任何野人的距离不会大于x，假设大于x，我们完全可以将那两个部落连起来，把那个和其他野人距离大于x的隔离得到一个部落
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN = 1e3 + 5;
int n, m, t;
int fa[MAXN];
int f[MAXN][21];
int d[MAXN];
int w[MAXN][21];
bool vis[MAXN];
int findf(int x) {
     
	if (x != fa[x]) fa[x] = findf(fa[x]);
	return fa[x];
}
struct Node {
     
	int x,y,id;
}node[MAXN];
struct Edge {
     
	Node a, b;
	double dis;
	bool operator<(const Edge& x) {
     
		return dis < x.dis;
	}
};
vector<Edge>e;
vector<Edge>edge;
double getdis(Node a, Node b) {
     
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int main() {
     
	cin >> n >> m;
	for (int i = 1;i <= n;i++) {
     
		cin >> node[i].x >> node[i].y;
		node[i].id = i;
	}
	for (int i = 1;i <= n;i++) {
     
		for (int j = 1;j <= n;j++) {
     
			if (i == j)continue;
			e.push_back({
      node[i],node[j],getdis(node[i],node[j]) });
		}
	}
	sort(e.begin(), e.end());
	int sz = e.size();
	for (int i = 1;i <= n;i++)fa[i] = i;
	for (int i = 0;i < sz;i++) {
     
		Edge now = e[i];
		int a = now.a.id;
		int b = now.b.id;
		double dis = now.dis;
		int z1 = findf(a), z2 = findf(b);
		if (z1 == z2)continue;
		fa[z1] = z2;
		edge.push_back({
      node[a],node[b],dis });
	}
	sort(edge.begin(), edge.end());
	int len = edge.size();
	double minn = edge[len - 1-(m-2)].dis;
	cout <<fixed<<setprecision(2)<< minn << endl;
}

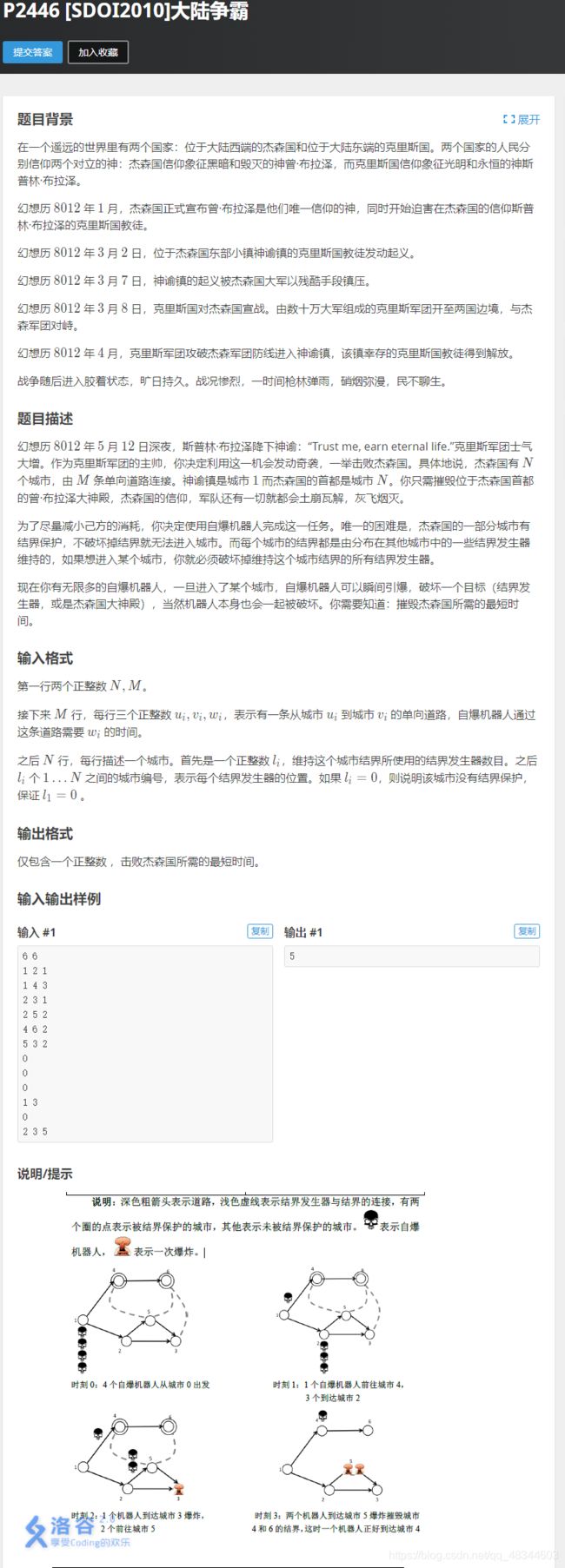
P2446 [SDOI2010]大陆争霸

//迪杰斯特拉+限制+类似是拓扑的算法
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAXN =3e3 + 5;
const int INF = 0x3f3f3f3f;
int n, m, t;
struct Edge {
     
	int from, to, w;
};
vector<Edge>edge[MAXN];
struct Node {
     
	int id, dis_n;
	bool operator<(const Node& a)const {
     
		return dis_n > a.dis_n;
	}
};
int dis[MAXN];
int arr[MAXN];
int into[MAXN];
bool isdone[MAXN];
vector<Edge>e[MAXN];
int in[MAXN];
bool vis[MAXN];
void dj() {
     
//我们的dis表示最终达到该店的最小距离，arr表示达到该点的距离（但是可能正在被守护着），into表示守护该点的所有点的最大距离
//所以我们dis=max(arr,into)
	memset(dis, 0x3f, sizeof dis);
	memset(arr, 0x3f, sizeof arr);
	priority_queue<Node>q;
	dis[1] = arr[1]=into[1]=0;
	q.push({
      1,0 });
	while (!q.empty()) {
     
		Node now = q.top();
		q.pop();
		int u = now.id;
		if (isdone[u])continue;
		isdone[u] = true;
		for (int i = 0;i < edge[u].size();i++) {
     
			int v = edge[u][i].to;
			int w = edge[u][i].w;
			if (isdone[v])continue;
			if (arr[v] > dis[u] + w) {
     
				arr[v] = dis[u] + w;//到达v点，但可能被守护着
				if (in[v] == 0) {
     //如果没被守护，或者守护全被打了
					dis[v] = max(into[v], arr[v]);//得到dis值
					q.push({
     v,dis[v]});
				}	
			}
		}
		for (int i = 0;i < e[u].size();i++) {
     //这是建立了守护的图，类似拓扑的算法
			int v = e[u][i].to;
			into[v] = max(into[v], dis[u]);//into表示的是守护v这点的城市已经被到达的距离
			in[v]--;//因为是守护的图，所以遍历u的边，v相当于少了个边
			if (in[v] == 0) {
     //如果这个点没守护了，我们就行判断他的距离
				dis[v] = max(arr[v], into[v]);//分为arr大与into大的情况，arr大（也可以是INF），表示我们从起点到那个点很远，我们把守护的城市都打了，还没有到，into大，就说明我们早就到了这个城市，但是守护他的很远，我们得先破掉守护他得
				q.push({
      v,dis[v] });
			}

		}
	}
}


int main() {
     
	std::ios::sync_with_stdio(false);
	cin >> n >> m;
	for (int i = 1;i <= m;i++) {
     
		int from, to, w;
		cin >> from >> to >> w;
		edge[from].push_back({
      from,to,w });
	}
	
	for (int i = 1;i <= n;i++) {
     
		int c;
		cin >> c;
		if (c == 0)continue;
		for (int j = 1;j <= c;j++) {
     
			int from;
			cin >> from;
			e[from].push_back({
     from,i,INF});
			in[i]++;
		}
	}
	dj();
	cout << dis[n] << endl;
}