P1351 联合权值（树形DP）

题目描述

无向连通图 G 有 n个点，n−1 条边。点从 1到 n依次编号,编号为 i 的点的权值为 Wi，每条边的长度均为 111。图上两点 (u,v) 的距离定义为 u点到 v点的最短距离。对于图 G上的点对 (u,v)，若它们的距离为 2，则它们之间会产生Wv×Wu的联合权值。

请问图 G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入格式

第一行包含 1 个整数 n。

接下来 n−1 行,每行包含 2个用空格隔开的正整数 u,v表示编号为 u和编号为 v的点之间有边相连。

最后 11行,包含 nnn 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图 G 上编号为 i的点的权值为 Wi。

输出格式

输出共 1 行,包含 2个整数，之间用一个空格隔开,依次为图 G上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007取余。

输入输出样例

输入 #1

5  
1 2  
2 3
3 4  
4 5  
1 5 2 3 10 

输出 #1

20 74

说明/提示

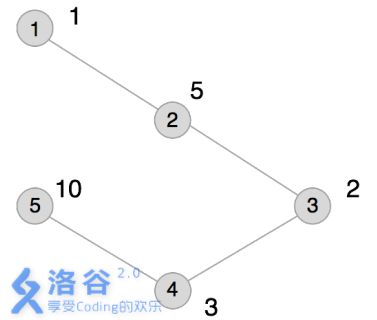
本例输入的图如上所示，距离为2 的有序点对有(1,3)( 1,3)(1,3) 、(2,4)( 2,4)(2,4) 、(3,1)( 3,1)(3,1) 、(3,5)( 3,5) (3,5)、(4,2)( 4,2)(4,2) 、(5,3)( 5,3) (5,3)。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30%的数据，1

对于60%的数据，1

对于100%的数据，1

保证一定存在可产生联合权值的有序点对。

题解

这道题的mod很毒瘤

1. maxans不能mod，因为题目中说了sumans比较大，要取模，而没有说maxans

2. 在计算过程中，sumans可能为负值，所以每次要单独再+mod%mod一下

做法的话，考虑这里的(u,v)是间隔为2的节点，那么我们首先可以想到60%（实际是70%）的做法：

枚举一个点i，找出他的邻接点adj1 和 邻接点的邻接点adj2，然后对adj1和adj2一通乱搞

100%的做法：

注意这里为了表示方便：fa也是son ，明白就好

对于节点u的儿子：son1,son2,....sonn

设其中最大的儿子和次大的儿子为 f_maxson  ,  s_maxson

则u的联合权值之和为  

这样理解：联合权值就是u的任意两个儿子两两组合的乘积，就得到上面的式子了，最后一项是为了除去自己和自己相同的情况

#include
#include
#include
#include
using namespace std;
const int N=200000*2+5;
const int mod=10007;
int head[N],nxt[N],adj[N],tot;
int w[N];
void add(int u,int v)
{
	tot++;
	nxt[tot]=head[u];
	head[u]=tot;
	adj[tot]=v;
}
inline long long mx(long long x,long long y)
{
	return x>y?x:y;
}
long long sumans,maxans;
void dfs(int u,int fa)
{
	long long sum_soni=0,sum_sona=0;
	int f_maxson=0,s_maxson=0;
	for(int i=head[u];i;i=nxt[i])
	{
		int v=adj[i];
		if(v!=fa)dfs(v,u);
		if(w[v]>s_maxson)
		{
			if(w[v]>f_maxson){s_maxson=f_maxson;f_maxson=w[v];}
			else s_maxson=w[v];
		}
		sum_sona+=1ll*w[v];
		sum_soni+=1ll*w[v]*w[v];
	}
	sumans+=((sum_sona%mod)*(sum_sona%mod)%mod-sum_soni%mod+mod)%mod;sumans=(sumans+mod)%mod;
	maxans=mx(maxans,(s_maxson*f_maxson));
}
int main()
{
	freopen("1351.in","r",stdin);
	freopen("1351.out","w",stdout);
	int n,i,x,y;
	scanf("%d",&n);
	for(i=1;i