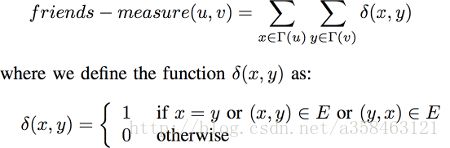社交网络中的Link Prediction
介绍
给你一段时间内的社交网络关系,我们能否预测出成员之间在未来的互动? 我们称该问题为Link prediction Problem.他还有另外一些常见的应用,比如社交网站的好友推荐,预测蛋白质间的相互影响,预测犯罪嫌疑人的关系,商品推荐等等。
在基于社交网络的Link predition问题中,我们通常要考虑社交网络所带有的特有的特质。所以我们先介绍一下社交网络的几个有趣的性质:
power law degree distribution
the small world phenomenon
the community structure (clustering effect)
etc
Power law degree distribution: 大部分人都只有很少的链接,但是有一小部分人,他们的链接的数量远远多于其他人。

Small-World Phenomenon: 或者叫六度空间,你和任何一个陌生人之间所间隔的人不会超过六个
community structure (clustering effect): 社交网络里面会有很多个小群体,他们都相互认识彼此。
那么到底要怎么去做link predction呢,目前传统的方法,有Path-based Methods,Neighbor-based Methods等等。下面是他们的介绍。
Path-based Methods
Graph Distance
一个最直接的预测方法就是计算两个结点间的距离,然后根据距离的大小来预测,两个结点越近那么就越容易在未来建立联系。但是在上百万的结点下直接用dijkstra算法是非常低效的。相反,我们可以利用small world phenomenon来提高我们的效率。
比如说要计算x,y两点距离,我们先初始化两个集合 S={x},D={y} S = { x } , D = { y } ,然后开始扩展S和D的集合,扩展的方法就是不断地把集合里面元素的邻居放进去,比如一开始就是把x的邻居放进集合S中,y的邻居放进D中,一直循环,直到S和D出现相同的元素为止。根据small world phenomenon来说,扩展的次数不会太多。另外效率起见,我们一般选择元素数量较少的那个来扩展。
Katz (Exponentially Damped Path Counts)
我们还可以考虑用x,y之间存在的路径的数量来衡量它们的距离。然而,路径有长有短,一般认为,那些很长的路径其实是没什么说服力的,于是引入指数衰减机制随着路径长度进行衰减。
β β 就是指数衰减的系数, pathl p a t h l 表示那些长度为l的路径。
Hitting Time
为了加快计算速度,可以使用蒙特卡洛的技术来估计x,y的路径的数量。从x出发,在附近随机的跳转,如果到达y,则记录下这次到达y的所需跳转次数。最后我们用 总跳转次数/到达y的次数 来表示距离。
其中 Hx,y H x , y 为总跳转次数/到达y的次数,我们取负H来表示评分,H越小表示越近则越好。
Rooted PageRank
然而,如果y是一个非常有影响力的人,那么很多人都能在非常少的跳转次数下到达y,为了减轻这效应,我们增加一个随机”reset”以及继续游走的机制。当到达y时,以概率 α α 跳回x,以 1−α 1 − α 继续随机游走。并记录下经过y的次数。
其中 πy π y 表示那么多次跳转经过y概率。
Neighbor-based Methods
Common Neighbors
当两个用户有着很多个相同的邻居,我们就认为这两个用户很有可能建立联系。所以两个用户的相似性就用他们相同邻居的数量表示:
其中 T(x) T ( x ) 表示x的邻居。实际上这个方法揭示了一个叫“closing a trangle”的现象
Jaccard’s Coefficient
然而Common Neighbors有一个很大的问题,假设有一个人有非常多的邻居,那么所有人都会倾向于预测跟他产生互动,为此,我们还要把他们邻居的数量考虑进去,于是我们认为,如果两个人共同邻居的数量在他们所有好友数量中占比越大,就认为可能建立联系。即
Adamic/Adar (Frequency-Weighted Common Neighbors)
这个方法同样是对Common Neighbors的改进,当我们计算两个相同邻居的数量的时候,其实每个邻居的“重要程度”都是不一样的,我们认为这个邻居的邻居数量越少,就越凸显它作为“中间人”的重要性,毕竟一共只认识那么少人,却恰好是x,y的好朋友。
Friendes-mearsure
既然两个人有相同的好友可以表达他们间的距离,那么我们可以把这一个思想推广,我们认为,他们的好友之间很有可能互为好友。我们就计算他们好友之间互为好友的数量作为评价标准。
Preferential Attachment
另外,如果两个用户拥有的好友数量越多,那么就越有可能更愿意去建立联系。也就是“富人越富”原则,基于这思想,用他们两个用户的好友数量的乘积作为评分。
Link Prediction with Personalized Social Influence
上面的方法只考虑了结构,现在介绍一种考虑了用户行为的方法,比如转发,评论,点赞等。
这里考虑一种低秩表达,S和T,使得未来会建立联系的用户i和用户j有,
其中(i,n)是那些不会建立联系的人。


用一个sigmoid函数来表达下一时刻会active的概率。这里的f使用了log函数,主要考虑了其影响是随着次数指数衰减的。
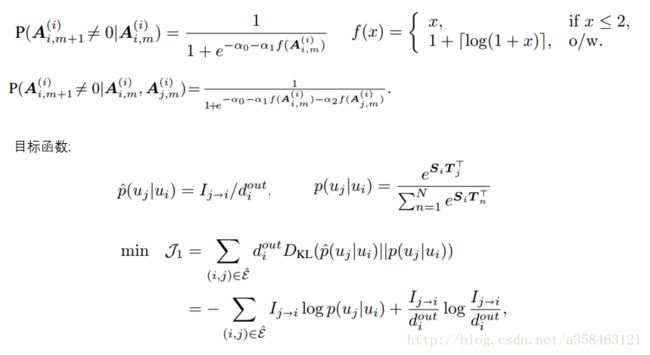
最后给出一个目标函数通过优化得到S和T。
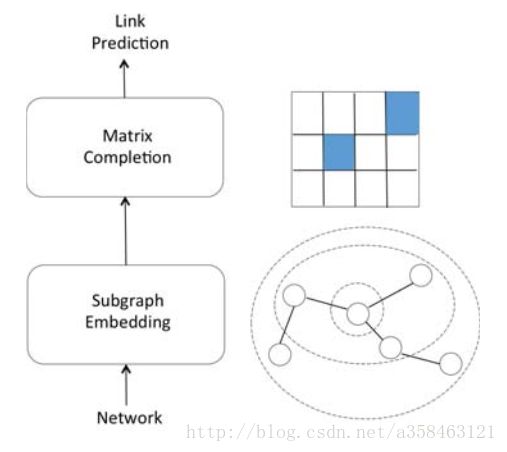
Link Prediction via Subgraph Embedding-Based Convex Matrix Completion
基本思想就是,每个结点,用广度优先搜索就可以得到不同深度的子图,然后利用这些结构信息来embedding,最后通过将不同深度得到的embedding concat在一起,就得到了这个结点的embedding. 最后就用这些embedding的余弦相似度来做link prediction.
References
What will Facebook friendships look like tomorrow?
Link Prediction via Subgraph Embedding-Based Convex Matrix Completion. *Zhu Cao, Linlin Wang, Gerard De melo.*AAAI 2018.
Link Prediction with Personalized Social Influence. Huo, Zepeng, Xiao Huang, Xia Hu. AAAI 2018。
作为分享主义者(sharism),本人所有互联网发布的图文均遵从CC版权,转载请保留作者信息并注明作者a358463121专栏:http://blog.csdn.net/a358463121,如果涉及源代码请注明GitHub地址:https://github.com/358463121/。商业使用请联系作者。