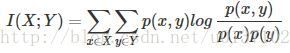TF-IDF
1. TF-IDF的原理
(1)为什么要进行TF-IDF处理
如果没有经过TF-IDF处理时,对下面的4个短文做了词频统计:
corpus=["I come to China to travel",
"This is a car polupar in China",
"I love tea and Apple ",
"The work is to write some papers in science"]
不考虑停用词,处理后得到的词向量如下:
[[0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 2 1 0 0]
[0 0 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0]
[1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0]
[0 0 0 0 0 1 1 0 1 0 1 1 0 1 0 1 0 1 1]]
如果我们直接将统计词频后的19维特征做为文本分类的输入,会发现有一些问题。比如第一个文本,我们发 现"come","China"和“Travel”各出现1次,而“to“出现了两次。似乎看起来这个文本与”to“这个特征更关系紧密。但是实际上”to“是一个非常普遍的词,几乎所有的文本都会用到,因此虽然它的词频为2,但是重要性却比词频为1的"China"和“Travel”要低的多。如果我们的向量化特征仅仅用词频表示就无法反应这一点。因此我们需要进一步的预处理来反应文本的这个特征,而这个预处理就是TF-IDF。
(2) TF-IDF的概述
TF-IDF是Term Frequency - Inverse Document Frequency的缩写,即“词频-逆文本频率”。它由两部分组成,TF和IDF。
前面的TF也就是我们前面说到的词频,我们之前做的向量化也就是做了文本中各个词的出现频率统计,并作为文本特征,这个很好理解。关键是后面的这个IDF,即“逆文本频率”如何理解。在上一节中,我们讲到几乎所有文本都会出现的"to"其词频虽然高,但是重要性却应该比词频低的"China"和“Travel”要低。我们的IDF就是来帮助我们来反应这个词的重要性的,进而修正仅仅用词频表示的词特征值。
概括来讲, IDF反应了一个词在所有文本中出现的频率,如果一个词在很多的文本中出现,那么它的IDF值应该低,比如上文中的“to”。而反过来如果一个词在比较少的文本中出现,那么它的IDF值应该高。比如一些专业的名词如“Machine Learning”。这样的词IDF值应该高。一个极端的情况,如果一个词在所有的文本中都出现,那么它的IDF值应该为0。
上面是从定性上说明的IDF的作用,那么如何对一个词的IDF进行定量分析呢?这里直接给出一个词xx的IDF的基本公式如下:
其中,NN代表语料库中文本的总数,而N(x)N(x)代表语料库中包含词xx的文本总数。为什么IDF的基本公式应该是是上面这样的而不是像N/N(x)这样的形式呢?这就涉及到信息论相关的一些知识了。感兴趣的朋友建议阅读吴军博士的《数学之美》第11章
上面的IDF公式已经可以使用了,但是在一些特殊的情况会有一些小问题,比如某一个生僻词在语料库中没有,这样我们的分母为0, IDF没有意义了。所以常用的IDF我们需要做一些平滑,使语料库中没有出现的词也可以得到一个合适的IDF值。平滑的方法有很多种,最常见的IDF平滑后的公式之一为:
有了IDF的定义,我们就可以计算某一个词的TF-IDF值了:
TF−IDF(x)=TF(x)∗IDF(x)TF−IDF(x)=TF(x)∗IDF(x)
其中TF(x)TF(x)指词xx在当前文本中的词频。
2.文本矩阵化,使用词袋模型,以TF-IDF特征值为权重。(可以使用Python中TfidfTransformer库)
实现文本矩阵化的方式有3种,分别是词袋模型、用CountVectorizer类和向量化之后再调用TfidfTransformer类进行预处理、直接用TfidfVectorizer完成向量化与TF-IDF预处理。
(1)词袋模型
1) 什么是词袋模型
词袋模型的主要的目的是找出进行分类建模的特征的找取,其步骤如下:
Bag-of-words词袋模型最初被用在信息检索领域,对于一篇文档来说,假定不考虑文档内的词的顺序关系和语法,只考 虑该文档是否出现过这个单词。假设有5类主题,我们的任务是来了一篇文档,判断它属于哪个主题。
a. 数据收集:在训练集中(主题类型已知)选择一些文档;
例如:
“It was the best of times,
it was the worst of times,
it was the age of wisdom,
it was the age of foolishness,”
b. 设计词汇:使用文档中的词来构建词袋;
•“it”
•“was”
•“the”
•“best”
•“of”
•“times”
•“worst”
•“age”
•“wisdom”
•“foolishness”
这是一个由包括24个词组成的语料库中其中包含10个词汇。
c. 创建文档向量
下一步是在每个文档中记录单词。目的是将自由文本的每个文档转换为一个文本向量,这样我们就可以将其用作机 器学习模型的输入或输出。
因为我们知道词汇有10,所以我们可以使用固定长度为10的文档,来表示向量中的每一个单词的位置。
最简单的设计方法是将单词的存在标记为布尔值,0表示缺席,1表示存在。使用我们的词汇表中列出的任意顺序排 列,我们可以通过第一个文档(“It was the best of times”),并将其转换为二进制向量。
d. 词汇管理
随着词汇量的增加,文档的向量表示也将随之增加。在前面的示例中,文档向量的长度等于已知单词的数量。你可以想象,对于一个非常大的语料库,比如成千上万的词汇量,向量的长度可能达到成千上万。此外,每个单一的文档可能包含词汇中已知的词汇量很少。
这就产生了很多零向量,称为稀疏向量(sparse vector)或稀疏表示(sparse representation)。
稀疏向量在建模时需要更多的内存和计算资源,大量的位置或维度使建模过程使用传统算法非常具有挑战性。
因此,当使用词袋(bag-of-words)模型时可以迫使其减小词汇量的大小。
解决办法:
(a)忽视案例、忽略标点符号、忽略没有太多信息的频繁单词(又被称为停止词),如“a”,“of”等、忽略没有太多信息的频繁单词(又被称为停止词),如“a”,“of”等。
(b)使用二元模型
例如,上一节的第一行文字中的双字:“It was the best of time”如下:
it was、“was the”、“was the”、“best of”、“of time”
2) 词袋模型的实现
(2) CountVectorizer类和向量化之后再调用TfidfTransformer
代码:
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer
corpus=["I come to China to travel",
"This is a car polupar in China",
"I love tea and Apple ",
"The work is to write some papers in science"]
vectorizer=CountVectorizer()
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(vectorizer.fit_transform(corpus))
print (tfidf)结果:
(0, 16) 0.4424621378947393
(0, 15) 0.697684463383976
(0, 4) 0.4424621378947393
(0, 3) 0.348842231691988
(1, 14) 0.45338639737285463
(1, 9) 0.45338639737285463
(1, 6) 0.3574550433419527
(1, 5) 0.3574550433419527
(1, 3) 0.3574550433419527
(1, 2) 0.45338639737285463
(2, 12) 0.5
(2, 7) 0.5
(2, 1) 0.5
(2, 0) 0.5
(3, 18) 0.3565798233381452
(3, 17) 0.3565798233381452
(3, 15) 0.2811316284405006
(3, 13) 0.3565798233381452
(3, 11) 0.3565798233381452
(3, 10) 0.3565798233381452
(3, 8) 0.3565798233381452
(3, 6) 0.2811316284405006
(3, 5) 0.2811316284405006(3)TfidfVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf2 = TfidfVectorizer()
re = tfidf2.fit_transform(corpus)
print re3.互信息的原理。
(1)点互信息
机器学习相关文献里面,经常会用到点互信息PMI(Pointwise Mutual Information)这个指标来衡量两个事物之间的相关性(比如两个词)
在概率论中,我们知道,如果x跟y不相关,则p(x,y)=p(x)p(y)。二者相关性越大,则p(x, y)就相比于p(x)p(y)越大。用后面 的 式子可能更好理解,在y出现的情况下x出现的条件概率p(x|y)除以x本身出现的概率p(x),自然就表示x跟y的相关程度。
举个自然语言处理中的例子来说,我们想衡量like这个词的极性(正向情感还是负向情感)。我们可以预先挑选一些正向情 感的词,比如good。然后我们算like跟good的PMI。
(2)互信息
用来评价一个事件的出现对于另一个事件的出现所贡献的信息量。
互信息即:
其衡量的是两个随机变量之间的相关性,即一个随机变量中包含的关于另一个随机变量的信息量。所谓的随机变量,即随 机试验结果的量的表示,可以简单理解为按照一个概率分布进行取值的变量,比如随机抽查的一个人的身高就是一个随机变 量。
可以看出,互信息其实就是对X和Y的所有可能的取值情况的点互信息PMI的加权和。因此,点互信息这个名字还是很形象 的。
4.使用第二步生成的特征矩阵,利用互信息进行特征筛选。
(1)特征筛选的原则
首先,‘无关特征’的过滤;比如:男女的比例和会不会下雨无关;
其次,‘多余特征’的过滤;比如:消费水平(税收水平)其中一个多余
(2) 利用互信息进行特征筛选
在对文本进行特征选择的时候,X表示某个词,Y表示类别,xi表示这个词的取值,在这里只有两种情况,出现和不出 现,yi表示某一类,可能两类可能多类。
xi 和yi同时出现在整个数据集中的概率:
联合概率
xi在 整个数据集中出现的概率:
词概率
yi在这个数据集中出现的概率:
类概率
对文本特征提取xi的取值只能是出现和不出现两种情况
使用互信息理论进行特征抽取是基于如下假设:在某个特定类别出现频率高,但在其他类别出现频率比较低的词条与该类的互信息比较大。通常用互信息作为特征词和类别之问的测度,如果特征词属于该类的话,它们的互信息量最大。由于该方法不需要对特征词和类别之问关系的性质作任何假设,因此非常适合于文本分类的特征和类别的配准工作。