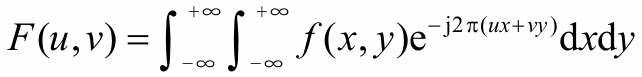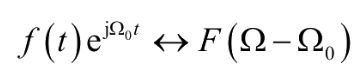图像基础——频率滤波

一维傅里叶变换

从物理效果看，傅立叶变换是将图像从空间域转换到频率域，傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。
图片在做完傅里叶变换后，每个角都是零频分量，所以要使用fftshift方法处理（相当于二四象限交换，一三象限交换），使得中间是低频，四周是高频。而中间的原点 是直流分量。

低频分量(低频信号)：代表着图像中亮度或者灰度值变化缓慢的区域，也就是图像中大片平坦的区域，描述了图像的主要部分，是对整幅图像强度的综合度量。

对应着图像变化剧烈的部分，也就是图像的边缘（轮廓）或者噪声以及细节部分。 主要是对图像边缘和轮廓的度量，而人眼对高频分量比较敏感。之所以说噪声也对应着高频分量，是因为图像噪声在大部分情况下都是高频的。

距离原点越远=频率越高=原图中灰度值的变化越频繁。
灰度值越大=幅值越大=原图中灰度值变化的范围越大。

相关数学公式

• 连续函数傅里叶正变换

• 连续函数傅里叶逆变换
  

• 离散函数傅里叶正变换
  

• 离散函数傅里叶逆变换
  

• 欧拉公式

• 相位、幅度、初相、频率

y = Asin(wx+r)
角速度：w
周期T = 2*pi/w
频率F = 1/T ，即一秒内完成周期性变换的次数
初相：r
相位：wx + r

画相关频谱图

将sin2*pi*x的单边频谱、双边频谱图画出。

import numpy as np
import matplotlib.pyplot as plt
# 生成单一正弦波，观看其频域上的函数
x = np.arange(0,5,0.005)
sin = np.sin(2*np.pi*x) #频率为1，角速度为2pi
y = np.fft.fft(sin)
def show(f,fft):
    n = 5  #采样区间
    interval = 0.005  #采样间隔
    fre = n/interval  #采样频率
    fft_y = np.abs(fft) / fre  #频率幅值归一化处理
    plt.figure(figsize=(10,5))
    plt.subplot(1,3,1)
    plt.plot(np.arange(0,n,interval),f)
    plt.xlabel('时间')
    plt.ylabel('振幅')
    plt.title('原始信号')
    plt.subplot(1,3,2)
    plt.plot(np.arange(fre),fft_y)
    plt.xlabel('频率')
    plt.ylabel('频幅')
    plt.title('双边振幅谱')
    plt.subplot(1,3,3)
    plt.plot(np.arange(fre/2),fft_y[range(int(fre/2))])
    plt.xlabel('频率')
    plt.ylabel('频幅')
    plt.title('单边振幅谱')
    plt.show()
show(sin,y)

继续上述代码，对3个正弦波形进行叠加，然后进行傅里叶变换。

# 生成单一正弦波，观看其频域上的函数
x = np.arange(0,5,0.005)
sin = np.sin(2*np.pi*x)
sin1 = np.sin(2*np.pi*20*x)
sin2 = np.sin(2*np.pi*60*x)
sin += sin1+sin2
y = np.fft.fft(sin)
show(sin,y)

下面生成方波的傅里叶频谱图。

x = np.zeros(1000)
x[::20] = 1
y = np.fft.fft(x)
show(x,y)

下面进行脉冲波的傅里叶变换

x = np.zeros(1000)
x[380:400] = np.arange(0,1,0.05)
x[400:420] = np.arange(1,0,-0.05)
y = np.fft.fft(x)
show(x,y)

二维傅里叶变换

相关数学公式

• 连续函数傅里叶正变换
  

从公式上可以看出，F(u,v)与f(x,y)与并不是一一对应的关系，F(u,v)所对应的不是某一个f（x，y）而是所有的f（x，y）与e^(-j2TT(ux/M+vy/N))的乘积的和。

• 连续函数傅里叶逆变换
  
• 离散函数傅里叶正变换
  
• 离散函数傅里叶逆变换
  

画相关频谱图

from skimage import data

camera = data.camera()
fft = np.fft.fft2(camera)
fft_shift = np.fft.fftshift(fft)  #默认中心点在左上角，转移至中心点
fft_y = np.log(np.abs(fft_shift))  #取模，用log函数映射
plt.figure(figsize=(9,9))
plt.subplot(1,2,1)
plt.imshow(camera, 'gray')
plt.title('原始图片')
plt.subplot(1,2,2)
plt.imshow(fft_y,'gray')
plt.title('傅里叶频谱')
plt.show()

上面就是我们经常看见的傅里叶谱，也叫功率图，越亮代表能量越大，幅角越大。垂直方向与水平方向都有白色的条纹，说明在垂直方向与水平方向低频部分很明显。

• 结论

傅里叶变换后的白色部分（即幅度较大的低频部分），表示的是图像中慢变化的特性，或者说是灰度变化缓慢的特性（低频部分）。
傅里叶变换后的黑色部分（即幅度低的高频部分），表示图像中快变化的特性，或者说是灰度变化快的特性（高频部分）。

傅里叶变换的性质

• 线性特性

若 f1(t)↔F1(Ω)，f2(t)↔F2(Ω)，则　af1(t)+bf2(t)↔aF1(Ω)+bF2(Ω)。

• 时延特性

若　f(t)↔F(Ω)，则：

时延（移位）特性说明波形在时间轴上时延，并不会改变信号幅度，仅使信号增加-Ωt0线性相位。

• 频移特性

若　f(t)↔F(Ω)，则

频移（调制）特性表明信号在时域中与复因子[插图]相乘，则在频域中将使整个频谱搬移Ω0。

• 尺度变换

若　f(t)↔F(Ω)，则

尺度特性说明，信号在时域中压缩，在频域中扩展；反之，信号在时域中扩展，在频域中就一定压缩；

• 时域微分特性
  

• 频域微分特性
  

• 时域卷积定理
  

两个时间函数的卷积运算变为两个频谱函数的相乘（代数）运算。

• 频域卷积定理
  

图像的频率滤波

频域滤波的基本步骤如下：

1. 对原始图像f(x,y)进行傅里叶变换得到F(u,v)
2. 将F(u,v)与传递函数H(u,v)进行卷积运算得到G(u,v)
3. 将G(u,v)进行傅里叶逆变换得到增强图像g(x,y)。

目前基于傅里叶变换的频域滤波主要包括低通滤波、高通滤波、带通滤波及同态滤波4类

低通滤波

理想低通滤波

理想低通滤波器的平滑作用非常明显，但由于变换有一个陡峭的波形，它的逆变换h(x,y)有强烈的振铃特性，使滤波后的图像产生模糊效果。因此，这种理想低通滤波在实际中并不采用。

from skimage import data,color

camera = color.rgb2gray(data.coffee())
fft = np.fft.fft2(camera)
fft_shift = np.fft.fftshift(fft)  #默认中心点在左上角，转移至中心点
D = 10   #截断频率
row,col = camera.shape
mask = np.zeros((row,col),np.uint8)
crow,ccol = int(row/2),int(col/2) #频谱中心点
for i in range(row):
    for j in range(col):
        if np.sqrt(i**2+j**2) <= D:
            mask[crow-D:crow+D,ccol-D:ccol+D] = 1
fft_shift = mask * fft_shift        
f_ishift = np.fft.ifftshift(fft_shift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)   #出来的是复数
img_back = (img_back-np.amin(img_back))/(np.amax(img_back)-np.amin(img_back))   #调整大小范围便于显示

Butterworth低通滤波器

与理想低通滤波器相比，高低频之间过渡较为平滑。


n=1时，过渡最平滑，即尾部包含有大量的高频成分，所以一阶Butterworth低通滤波器没有振铃现象；但随着n的增加，振铃现象会越来越明显。

高通滤波

理想高通滤波

理想高通滤波器的形状与低通滤波器的形状正好相反，其传递函数为：

camera = color.rgb2gray(data.coffee())
fft = np.fft.fft2(camera)
fft_shift = np.fft.fftshift(fft)  #默认中心点在左上角，转移至中心点
print(fft_shift)
print(fft_shift.shape)
D = 30
row,col = camera.shape
mask = np.zeros((row,col),np.uint8)
crow,ccol = int(row/2),int(col/2) #频谱中心点
mask[crow-D:crow+D,ccol-D:ccol+D] = 1
mask = 1- mask
fft_shift = mask * fft_shift        
f_ishift = np.fft.ifftshift(fft_shift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)   #出来的是复数
img_back = (img_back-np.amin(img_back))/(np.amax(img_back)-np.amin(img_back))   #调整大小范围便于显示

留下的遗问

1、对图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图？
2、距离原点越远，则说明频率越大。因此，窗口边缘处即为高频区域，原点周边即为低频区域。？源于这里