一文讲清楚动物模型中的母体效应
母体效应
母亲对后代生活环境的影响(泌乳能力,母性等),就是母亲带来的效应。
俗话说:“父挫,挫一个;母挫,挫一窝”。因为,母性效应很强大,母亲的影响力要甩父亲几条街。从遗传的角度,想要改良家族的基因和性格,男性找一个好的女性做配偶,比女性找一个好的男性做配偶,影响要更大。
想到这里,忽然感觉结婚时,给女方大量的彩礼,也可以理解了。
女性对后代影响大,不只是从遗传的角度,还有环境的作用,还有交互的作用,更别提还有线粒体遗传呢!
我一直对个体永久环境效应,母体遗传效应,母体永久环境效应傻傻分不清楚,构建模型时,总是知其然而不知其所以然,这种一瓶子不满半瓶子咣当的状态显然不是一个段子说得好的数据分析师应该具备的素养。
所以,
我就写篇博客介绍一下,顺便理清一下自己的思路。毕竟,你如果不炫富,别人怎么知道你有钱呢?你如果带着口罩,别人怎么知道你帅呢?你如果不看时间,别人怎么知道你有劳力士呢?你如果不写出来,怎么知道你有两把刷子呢?(高考作为排比句系列)
所以,
我就写博客,证明一下自己是一个有劳力士会讲段子帅气的数据分析师。
1. 几个概念
- 个体永久环境效应(Individual permanent environmental effect),也称为永久环境效应,一般是个体有重复值时可以将其剖分出来,比如鸡产蛋,猪产仔等。
- 母体遗传效应(Maternal genetic effect),一般我们将个体加性效应称为个体加性遗传效应,因为它会考虑个体间亲缘关系矩阵(A或者G或者H矩阵),如果母体作为随机因子,也考虑亲缘关系矩阵,就称为母体遗传效应。
- 母体环境效应(Maternal permanent environmental effect),也称为母体永久环境效应,在分析时作为随机因子,但是不考虑亲缘关系矩阵。
2. 母体效应包括两种
第一种:母体遗传效应,这里母体遗传效应也分为两种,一种是考虑母体遗传效应和个体加性效应协方差,一种是不考虑,不过默认都是考虑的。
第二种:母体环境效应,就是不考虑情缘关系矩阵,作为随机因子的那种模型。
3. 第一种:母体遗传效应
3.1 考虑母体遗传效应和个体加性效应协方差
模型书写:
y = X b + Z a + Z m g + e y = Xb + Za + Zm_g + e y=Xb+Za+Zmg+e
这里:
- Xb为固定因子
- Za为随机因子,个体加性效应
- Zm_g为随机因子,母体遗传效应
- e为残差
方差协方差结构:
G = V a r [ a m g ] = [ A σ a 2 A σ a m A σ a m A σ m g 2 ] G = Var\begin{bmatrix} a\\m_g \end{bmatrix} = \begin{bmatrix} A\sigma_a^2 & A\sigma_{am} \\ A\sigma_{am} & A\sigma_{m_g}^2\end{bmatrix} G=Var[amg]=[Aσa2AσamAσamAσmg2]
这里A为亲缘关系矩阵,可以看出加性和母体存在协方差,而且加性和母体都要考虑A矩阵。
示例数据+示例代码+示例结果
数据和代码:
# 载入软件包
# devtools::install_github("dengfei2013/learnasreml")
library(learnasreml)
# asreml属于商业版软件,需要购买,购买请联系:http://www.vsnc.com.cn/
library(asreml)
data("animalmodel.dat")
data("animalmodel.ped")
head(animalmodel.dat)
head(animalmodel.ped)
# m1 单性状动物模型
dat = animalmodel.dat
ped = animalmodel.ped
dat[dat==0] = NA
str(dat)
# 计算亲缘关系逆矩阵
# m1 单性状动物模型 + 母体遗传效应 + 加性效应和母体遗传效应互作
m1 = asreml(BWT ~ SEX + BYEAR, random= ~ str(~vm(ANIMAL,ainv) + vm(MOTHER,ainv), ~us(2):vm(ANIMAL,ainv)),
residual = ~ idv(units),data = dat)
summary(m1)$varcomp
vpredict(m1,h2 ~ V1/(V1+V2+V3+V4))
结果:
> summary(m1)$varcomp
component std.error z.ratio bound %ch
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!us(2)_1:1 1.66469827 0.9069349 1.8355213 P 0.0
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!us(2)_2:1 0.01602755 0.4968458 0.0322586 P 0.8
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!us(2)_2:2 1.35818328 0.4194201 3.2382408 P 0.0
units!units 2.19186868 0.6632651 3.3046644 P 0.0
units!R 1.00000000 NA NA F 0.0
> vpredict(m1,h2 ~ V1/(V1+V2+V3+V4))
Estimate SE
h2 0.3182506 0.1714373
从结果可以看出:
- 加性方差组分:1.665
- 加性和母体遗传协方差组分:0.016
- 母体遗传方差组分:1.35
- 残差方差组分:2.19
由此计算的遗传力为0.318
3.2 不考虑母体遗传效应和个体加性效应协方差
模型书写:
y = X b + Z a + Z m g + e y = Xb + Za + Zm_g + e y=Xb+Za+Zmg+e
这里:
- Xb为固定因子
- Za为随机因子,个体加性效应
- Zm_g为随机因子,母体遗传效应
- e为残差
方差协方差结构:
G = V a r [ a m g ] = [ A σ a 2 0 0 A σ m g 2 ] G = Var\begin{bmatrix} a\\m_g \end{bmatrix} = \begin{bmatrix} A\sigma_a^2 & 0\\ 0 & A\sigma_{m_g}^2\end{bmatrix} G=Var[amg]=[Aσa200Aσmg2]
这里A为亲缘关系矩阵,可以看出,不考虑加性和母体协方差,而且加性和母体都要考虑A矩阵。
示例数据+示例代码+示例结果
这里,将us变为diag,即不考虑协方差。
m2.1 = asreml(BWT ~ SEX + BYEAR, random= ~ str(~vm(ANIMAL,ainv) + vm(MOTHER,ainv), ~diag(2):vm(ANIMAL,ainv)),
residual = ~ idv(units),data = dat)
summary(m2.1)$varcomp
vpredict(m2.1,h2 ~ V1/(V1+V2+V3))
结果:
> summary(m2.1)$varcomp
component std.error z.ratio bound %ch
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!diag(2)_1 1.689122 0.5291361 3.192225 P 0.0
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!diag(2)_2 1.366709 0.3151848 4.336215 P 0.1
units!units 2.174346 0.3932961 5.528523 P 0.0
units!R 1.000000 NA NA F 0.0
> vpredict(m2.1,h2 ~ V1/(V1+V2+V3))
Estimate SE
h2 0.3229569 0.09621066
从结果可以看出:
- 加性方差组分:1.68
- 母体遗传方差组分:1.36
- 残差方差组分:2.17
由此计算的遗传力为0.32
另外一种写法:
可以和加性方差组分写法类似,直接用vm函数,这种写法比较简单,但是没有考虑加性和母体遗传效应的协方差。
# m2 单性状动物模型 + 母体遗传效应
m2.2 = asreml(BWT ~ SEX + BYEAR, random= ~ vm(ANIMAL,ainv) + vm(MOTHER,ainv),
residual = ~ idv(units),data = dat)
summary(m2.2)$varcomp
vpredict(m2.2,h2 ~ V1/(V1+V2+V3))
> summary(m2.2)$varcomp
component std.error z.ratio bound %ch
vm(ANIMAL, ainv) 1.689188 0.5292161 3.191868 P 0
vm(MOTHER, ainv) 1.366777 0.3153196 4.334578 P 0
units!units 2.174264 0.3932864 5.528448 P 0
units!R 1.000000 NA NA F 0
> vpredict(m2.2,h2 ~ V1/(V1+V2+V3))
Estimate SE
h2 0.3229663 0.09621819
可以看到结果完全一样。
4. 第二种:母体环境效应
模型书写:
y = X b + Z a + Z m + e y = Xb + Za + Zm + e y=Xb+Za+Zm+e
这里:
- Xb为固定因子
- Za为随机因子,个体加性效应
- Zm为随机因子,母体环境效应
- e为残差
方差协方差结构:
G = V a r [ a m g ] = [ A σ a 2 0 0 I σ m g 2 ] G = Var\begin{bmatrix} a\\m_g \end{bmatrix} = \begin{bmatrix} A\sigma_a^2 & 0\\ 0 & I\sigma_{m_g}^2\end{bmatrix} G=Var[amg]=[Aσa200Iσmg2]
这里A为亲缘关系矩阵,可以看出,不考虑加性和母体协方差,而且加性和考虑A矩阵,母体不考虑A矩阵。
这里的母体环境效应,不考虑亲缘关系矩阵,将其作为随机因子即可。
# m3 单性状动物模型 + 母体环境效应
m3 = asreml(BWT ~ SEX + BYEAR, random= ~ vm(ANIMAL,ainv) + MOTHER,
residual = ~ idv(units),data = dat)
summary(m3)$varcomp
vpredict(m3,h2 ~ V1/(V1+V2+V3))
结果:
> summary(m3)$varcomp
component std.error z.ratio bound %ch
MOTHER 1.104038 0.2398000 4.603997 P 0
vm(ANIMAL, ainv) 2.277785 0.4970861 4.582274 P 0
units!units 1.656900 0.3734446 4.436803 P 0
units!R 1.000000 NA NA F 0
> vpredict(m3,h2 ~ V1/(V1+V2+V3))
Estimate SE
h2 0.2191107 0.04364284
5. 同时考虑母体遗传效应和母体环境效应
模型书写:
y = X b + Z 1 a + Z 2 m g + Z 3 m e + e y = Xb + Z_1a + Z_2m_g +Z_3m_e + e y=Xb+Z1a+Z2mg+Z3me+e
这里:
- Xb为固定因子
- Za为随机因子,个体加性效应
- Zm_g为随机因子,母体遗传效应
- Zm为随机因子,母体环境效应
- e为残差
方差协方差结构:
G = V a r [ a m g m e ] = [ A σ a 2 A σ a m 0 A σ a m A σ m g 2 0 0 0 I σ m e 2 ] G = Var\begin{bmatrix} a\\m_g \\m_e \end{bmatrix} = \begin{bmatrix} A\sigma_a^2 & A\sigma_{am} & 0 \\ A\sigma_{am} & A\sigma_{m_g}^2 & 0 \\0 & 0 & I\sigma_{m_e}^2\end{bmatrix} G=Var⎣⎡amgme⎦⎤=⎣⎡Aσa2Aσam0AσamAσmg2000Iσme2⎦⎤
# m4 单性状动物模型 + 母体遗传效应 + 加性效应和母体遗传效应互作 + 母体环境效应
m4 = asreml(BWT ~ SEX + BYEAR, random= ~ str(~vm(ANIMAL,ainv) + vm(MOTHER,ainv), ~us(2):vm(ANIMAL,ainv)) + MOTHER,
residual = ~ idv(units),data = dat)
summary(m4)$varcomp
vpredict(m4,h2 ~ V1/(V1+V2+V3+V4+V5))
结果:
> summary(m4)$varcomp
component std.error z.ratio bound %ch
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!us(2)_1:1 1.688055506 0.9091111 1.85681974 P 0.0
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!us(2)_2:1 0.006385884 0.4954503 0.01288905 P 4.0
vm(ANIMAL, ainv)+vm(MOTHER, ainv)!us(2)_2:2 1.057027088 0.4405431 2.39937292 P 0.1
MOTHER 0.497693182 0.3694028 1.34729116 P 0.6
units!units 2.157268745 0.6628453 3.25455845 P 0.0
units!R 1.000000000 NA NA F 0.0
> vpredict(m4,h2 ~ V1/(V1+V2+V3+V4+V5))
Estimate SE
h2 0.3122311 0.1665252
5. 基因组选择的应用母体遗传效应?
GBLUP或者SSGBLUP(一步法)的好处是,传统动物模型能用的模型,基因组选择都可以使用。一些性状在分析时,需要考虑重复力模型,母体遗传,母体环境等模型,分析结果会更准确。
6. 终于填坑完成
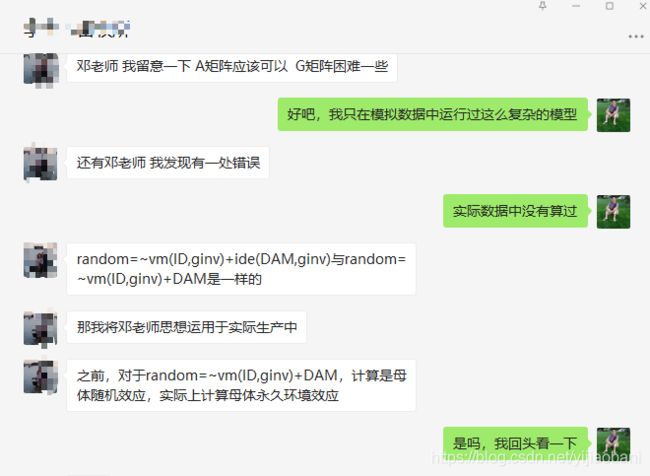
很多老师和同学和我交流,询问如何计算母体效应,如何计算母体遗传效应,如何计算母体环境效应,如何计算个体加性效应和母体遗传效应的交互等等,这次这篇博客一次性讲清楚了。
还有同学告诉我, 我之前的培训教程中,计算的母体效应,其实是母体环境效应(仅仅将母体作为随机因子,没有考虑系谱亲缘关系矩阵),我说我知道了,回头我写篇博客解释汇总一下。我看了一下聊天记录:2020年5月10号,这位同学,久等了。
7. 参考文献
张勤老师 2020年暑期summer school 统计遗传学暑期学校教材,中国农业大学
Lawrence R. Schaeffer, Linear Models and Animal Breeding, 2010
A R Gilmour, ASReml User Guide Release 4.1 Structural Specification, 2015
D G Butler, ASReml-R Reference Manual Version, 2018
终于写完了,赶紧三连吧,点赞,在看,发朋友圈。