OpenCV图像处理—— 滤波与模糊操作

        过滤可以移除图像中的噪音、提取感兴趣的可视特征、允许图像重采样等等。

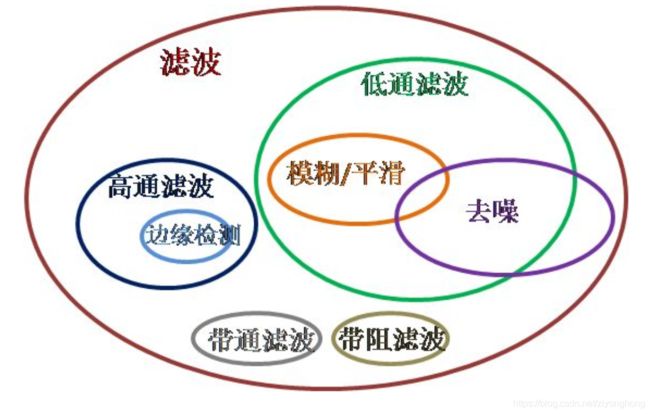
        频域分析将图像分成从低频到高频的不同部分。低频对应图像强度变化小的区域，而高频是图像强度变化非常大的区域。在频率分析领域的框架中，滤波器是一个用来增强图像中某个波段或频率并阻塞（或降低）其他频率波段的操作。滤波是对输入信号进行卷积处理的一个过程。

        模糊操作其实就是对每一个像素都取周边像素的平均值。

 

一、均值/中值/用户自定义模糊

      图片中一个方块区域（一般为3*3）内，中心点的像素为全部点像素值的平均值。均值滤波就是对于整张图片进行以下操作：

    均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。

   中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。

#均值模糊、中值模糊、自定义模糊    模糊是卷积的一种表象
import cv2 as cv
import numpy as np

def blur_demo(image):      #均值模糊  去随机噪声有很好的去燥效果
    dst = cv.blur(image, (1, 15))    #（1, 15）是垂直方向模糊，（15， 1）还水平方向模糊
    cv.namedWindow('blur_demo', cv.WINDOW_NORMAL)
    cv.imshow("blur_demo", dst)

def median_blur_demo(image):    # 中值模糊  对椒盐噪声有很好的去燥效果
    dst = cv.medianBlur(image, 5)
    cv.namedWindow('median_blur_demo', cv.WINDOW_NORMAL)
    cv.imshow("median_blur_demo", dst)

def custom_blur_demo(image):    # 用户自定义模糊
    kernel = np.ones([5, 5], np.float32)/25   #除以25是防止数值溢出
    dst = cv.filter2D(image, -1, kernel)
    cv.namedWindow('custom_blur_demo', cv.WINDOW_NORMAL)
    cv.imshow("custom_blur_demo", dst)

src = cv.imread('F:/Desktop/image/a.JPG')
cv.namedWindow('input_image', cv.WINDOW_NORMAL)
cv.imshow('input_image', src)

blur_demo(src)
median_blur_demo(src)
custom_blur_demo(src)

cv.waitKey(0)
cv.destroyAllWindows()

 

二、高斯模糊

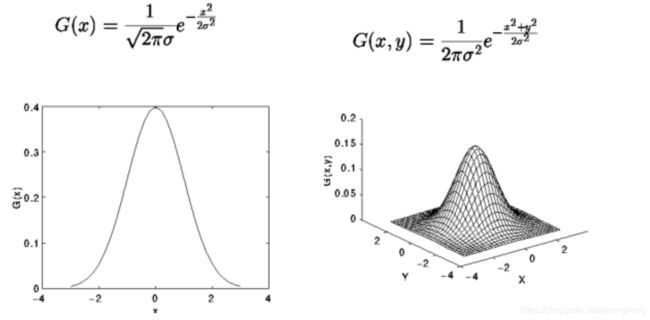
高斯模糊实质上就是一种均值模糊，只是高斯模糊是按照加权平均的，距离越近的点权重越大，距离越远的点权重越小。

高斯分布的一维和二维原理如下：

　补：高斯分布的标准差σ代表着数据的离散程度。如果σ较小，那么生成的模板的中心系数较大，而周围的系数较小，这样对图像的平滑效果就不是很明显；反之，σ较大，则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显。

 

#高斯模糊    轮廓还在，保留图像的主要特征  高斯模糊比均值模糊去噪效果好
import cv2 as cv
import numpy as  np


def clamp(pv):
    if pv > 255:
        return 255
    if pv < 0:
        return 0
    else:
        return pv

def gaussian_noise(image):
    h, w, c = image.shape
    for row in range(h):
        for col in range(w):
            s=np.random.normal(0,20,3)
            b = image[row, col, 0]  # blue
            g = image[row, col, 1]  # green
            r = image[row, col, 2]  # red
            image[row, col, 0] = clamp(b + s[0])
            image[row, col, 1] = clamp(g + s[1])
            image[row, col, 2] = clamp(r + s[2])
        cv.namedWindow("noise image", cv.WINDOW_NORMAL)
        cv.imshow("noise image", image)
        #ksize参数表示高斯滤波器模板大小。 ksize.width和ksize.height可以不同，
        # 但它们都必须是正数和奇数。或者，它们可以是零，即（0, 0），然后从σ计算出来。
        dst=cv.GaussianBlur(image,(15,15),0) #高斯模糊
        cv.namedWindow("Gaussian", cv.WINDOW_NORMAL)
        cv.imshow("Gaussian", dst)


src = cv.imread('F:/Desktop/image/a.JPG')
cv.namedWindow('input_image', cv.WINDOW_NORMAL)
cv.imshow('input_image', src)

gaussian_noise(src)
cv.waitKey(0)
cv.destroyAllWindows()

 

三、边缘保留滤波EPF

　　进行边缘保留滤波通常用到两个方法：高斯双边滤波和均值迁移滤波。

       双边滤波（bilateral filtering）的基本思路是同时考虑将要被滤波的像素点的空域信息（domain）和值域信息（range）。因此是一种非线性滤波方式，即同时考虑两方面的信息。

        图像在空间中变化缓慢，因此相邻的像素点会更相近。但是这个假设在图像的边缘处变得不成立。如果在边缘处也用这种思路来进行滤波的话，即认为相邻相近，则得到的结果必然会模糊掉边缘。因此考虑再利用像素点的值的大小进行补充，因为边缘两侧的点的像素值差别很大，因此会使得其加权的时候权重具有很大的差别，从而使得只考虑自己所属的一边的邻域。

      可以理解成先根据像素值对要用来进行滤波的邻域做一个分割或分类，再给该点所属的类别相对较高的权重，然后进行邻域加权求和，得到最终结果。

 

      meanShfit均值漂移算法是一种通用的聚类算法，它的基本原理是：对于给定的一定数量样本，任选其中一个样本，以该样本为中心点划定一个圆形区域，求取该圆形区域内样本的质心，即密度最大处的点，再以该点为中心继续执行上述迭代过程，直至最终收敛。

  

#边缘保留滤波（EPF）  高斯双边、均值迁移
import cv2 as cv
import numpy as np

def bi_demo(image):   #双边滤波
  #  bilateralFilter(src, d, sigmaColor, sigmaSpace)
  #src :处理的图形   d：在过滤期间使用的每个像素邻域的直径。
  #sigmaColor：色彩空间的标准方差，一般尽可能大。  sigmaSpace：坐标空间的标准方差(像素单位)，一般尽可能小。
    dst = cv.bilateralFilter(image, 0, 100, 15)
    cv.namedWindow("bi_demo", cv.WINDOW_NORMAL)
    cv.imshow("bi_demo", dst)

def shift_demo(image):   #均值迁移
   # pyrMeanShiftFiltering(src, sp, sr[, dst[, maxLevel[, termcrit]]])
   '''src:输入图像，8位，三通道图像。
     sp:漂移物理空间半径大小。
     sr:漂移色彩空间半径大小。
     dst:和源图象相同大小、相同格式的输出图象。
     maxLevel:金字塔的最大层数。
     termcrit:漂移迭代终止条件。'''

   dst = cv.pyrMeanShiftFiltering(image, 10, 50)
   cv.namedWindow("shift_demo", cv.WINDOW_NORMAL)
   cv.imshow("shift_demo", dst)
   

src = cv.imread('F:/Desktop/image/a.JPG')
cv.namedWindow('input_image', cv.WINDOW_NORMAL)
cv.imshow('input_image', src)

bi_demo(src)
shift_demo(src)

cv.waitKey(0)
cv.destroyAllWindows()