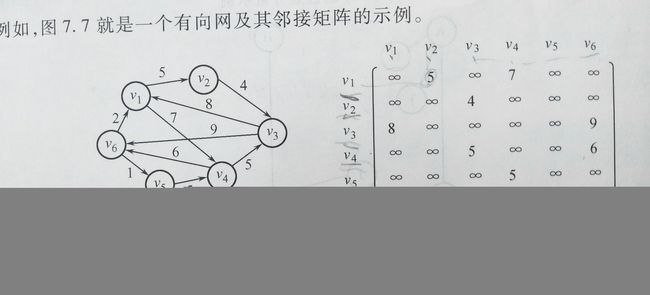
图的基础知识

顶点：Vertex
弧：Arc
弧尾：Tail
弧头：Head
A—>B(A是弧尾，B是弧头）
邻接：Adj
图：Graph

顶点v的度：是指和v相关联的边的数目
入度：以v为弧头的弧的数目
出度：以v为弧尾的弧的数目

邻接矩阵表示法：
采用两个数组来表示图：一个是用于存储顶点信息的一维数组，一个是用于存储图中顶点之间关联关系的二维数组，这个关联关系数组被称作邻接矩阵。

邻接矩阵和关联矩阵：
关联矩阵：m行n列，m表示顶点数，n表示弧数；关联矩阵每一行1的个数表示该顶点的度。
邻接矩阵：n行n列，n表示顶点数；该矩阵是一个对称矩阵，上三角和下三角镜面对称。
矩阵中的0和1可以被权值替代，达不到的边用无穷表示。

两个图：

两个图的邻接矩阵：

有向网及其邻接矩阵：

邻接矩阵表示法的定义C语言描述：

#define MAX_VERTEX_NUM 20  //最多顶点数 
#define INFINITY 32768  // 表示无穷 

typedef enum{DG,DN,UDG,UDN} GraphKind;  //图的种类 
typedef char VertexData;  //设立顶点数据为字符类型
typedef struct ArcNode{
	AdjType adj;  //弧的信息，要么是0值要么是1值 ,要么是权值 ，要么是无穷
	OtherInfo info;//弧的其他信息 
}ArcNode;
typedef struct {
	VertexData vertex[MAX_VERTEX_NUM]; //顶点的一维数组
	ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//邻接矩阵
	int vexnum;
	int arcnum;//图的顶点数和弧数
	GraphKind kind; //定义GraphType型的一个变量kind ，kind可以有四种情况 
}AdjMatrix;//邻接矩阵表示法

特殊说明这一句：typedef enum{DG,DN,UDG,UDN} GraphKind; //图的种类
这是枚举类型，
就像typedef char Datatype; 自定义一个类型Datatype,它代替了char型
typedef enum GraphKind; 自定义一个类型GraphKind,它代替了枚举类型enum,枚举了四种DG,DN,UDG,UDN，分别表示有向图，有向网，无向图，无向网。

采用邻接矩阵表示法创建有向图：

int LocateVertex(AdjMatrix *G,VertexData v)//求顶点的位置，在一维数组中找 
{
	int j=Error;
	int k;
	for(k=0;kvexnum;k++)
	{
		if(G->vertex[k]==v)
		{
			j=k;
			break;
		}
	}
	return j;
}

int CreateDN(AdjMatrix *G)  //创建一个有向网 
{
	int i,j,k;
	int weight;//权值 
	VertexData v1,v2;//顶点 
	scanf("%d%d",&G->arcnum,&G->vexnum);//输入弧数和点数 
	for(i=0;ivexnum;i++)
	{
		for(j=0;jvexnum;j++)
		{
			G->vertex[i][j].adj=INFINITY;//初始化每条弧的权值为无穷 
		}
	}
	for(i=0;ivernum;i++)
	{
		scanf("%c",&G->vertex[i]);//依次输入图的顶点数 
	}
	for(k=0;karcnum;k++)
	{
		scanf("%c,%c,%d",&v1,&v2,&weight);//输入两个顶点以及权值 
		i=LocateVextex(G,v1);//在一维数组中找到两个顶点 
		j=LocateVextex(G,v2);
		G->arcs[i][j].adj=weight;//将权值赋在两点间的弧上 
	}
	return(ok);
} 

结构体的定义

typedef struct ArcNode{
    int num;//权值 
    struct ArcNode *next;//指针域，存放具有相同出发点的弧 
}ArcNode;//弧结点 
typedef struct VNode{
    ArcNode *firstarc;//以该顶点为出发点的第一条弧 
}VNode;//顶点结点 
typedef struct Graph {
    VNode VNodeList[maxsize];//单链表 
    int n,e;//n是顶点数，e是弧数 
}Graph;//图 

创建图：

void bulidGraph(Graph *&g)
{
    g->n=6;
    g->e=7;
 
    VNode v0,v1 ,v2, v3 ,v4 ,v5,v6;//定义七个顶点 
    ArcNode *v01,*v03,*v04,*v14,*v12,*v20,*v32,*v56;//定义八条弧 
 
    v01=(ArcNode *) malloc(sizeof(ArcNode));
    v01->num=1;
    v03=(ArcNode *) malloc(sizeof(ArcNode));
    v03->num=3;
    v04=(ArcNode *) malloc(sizeof(ArcNode));
    v04->num=4;
    v14=(ArcNode *) malloc(sizeof(ArcNode));
    v14->num=4;
    v12=(ArcNode *) malloc(sizeof(ArcNode));
    v12->num=2;
    v20=(ArcNode *) malloc(sizeof(ArcNode));
    v20->num=0;
    v32=(ArcNode *) malloc(sizeof(ArcNode));
    v32->num=2;
    v56=(ArcNode *) malloc(sizeof(ArcNode));
    v56->num=6;
 
    v0.firstarc=v01;
    v1.firstarc=v14;
    v2.firstarc=v20;
    v3.firstarc=v32;
    v4.firstarc=NULL;
    v5.firstarc=v56;
    v6.firstarc=NULL;
 
    v01->next=v03;
    v03->next=v04;
    v14->next=v12;
    v32->next=NULL;
    v20->next=NULL;
    v12->next=NULL;
    v04->next=NULL;
    v56->next=NULL;
 
    g->VNodeList[0]=v0;
    g->VNodeList[1]=v1;
    g->VNodeList[2]=v2;
    g->VNodeList[3]=v3;
    g->VNodeList[4]=v4;
    g->VNodeList[5]=v5;
    g->VNodeList[6]=v6;
 
}

所显示出来的图：