基于C的查找算法
关键字:列表中数据元素的某一个数据项的值,(在数据库中又叫做码)用它可以区分数据元素的不同,该数据元素又可以称为是记录或者是元组(数据库基础,数据元素中包含很多个数据项,例如
学生(学号,性别,专业)其中学号就是关键字,唯一标识一个数据元素)
查找:查找列表中某个数据元素的数据项的值,与关键字一致。
查找算法分为三大类:
基于线性表查找法:顺序查找,折半查找,分块查找
基于树的查找法:二叉排序树,平衡二叉排序树,B树
计算式查找法:哈希法
基于线性表查找法:
==顺序查找算法==:存储结构通常用顺序结构,也可为链式结构
这里采用顺序结构
>**【算法思想】:在表的一端设置一个称为 “监视哨” 的附加单元,用来存放待查找元素的关键字。从表的另一端开始查找,如果在“监视哨”找到要查找元素的关键字,则返回失败的信息,否则返回相应下标**
**监视哨的作用:防止越界**
**首先定义一个数据类型:**
#define LINK_SIZE 20
typedef int KeyType;
typedef int OtherType;//用新定义的两种类型代替int型,方便以后更换为其他类型
typedef struct
{
KeyType key;
OtherType other_data;
}Recordtype;//记录的类型
typedef struct
{
Recordtype r[LINK_SIZE+1];//r[0]为监视哨单元
int len;
}RecordList;
变量other_data就相当于数据元素中除关键字以外的数据项
其次,在顺序表上查找元素
int seq_search(KeyType k,RecordList * st) //k用的是KeyType定义
{
int j;
j=st->len; //顺序表元素的个数
st->r[0].key=k; //st->r[0]单元作为监视哨
while(st->r[j].key!=k) //顺序表从后向前查找
j--;
return j; //j=0,找不到,j<>0,找到
}
while括号里需要的是前提条件,条件为真,继续执行循环;条件为假,跳出循环。
最后就是main函数
int main()
{
RecordList a;
int i,k;
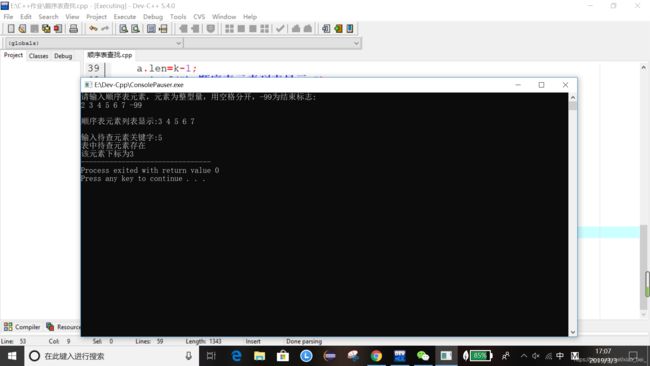
printf("请输入顺序表元素,元素为整型量,用空格分开,-99为结束标志:");
k=0;
scanf("%d",&i);/*得在循环条件之前先输入一个i,作为第一个值,进入到循环中。
如果没有这一句话 ,那么,后面的条件循环中的语句怎么摆放都是不正确的*/
while(i!=-99)
{
a.r[k++].key=i;//每一个数据元素都有关键字 ,这里的other_data没有表示
scanf("%d",&i);
}
a.len=k-1;
printf("\n顺序表元素列表显示:");
for(i=1;i<=a.len;i++)
{
printf("%d ",a.r[i].key);
}
printf("\n");
printf("\n输入待查元素关键字:");
scanf("%d",&i);
k=seq_search(i,&a);
if(k==0)
{
printf("表中待查元素不存在\n\n");
}
else
{
printf("表中待查元素存在\n");
printf("该元素下标为%d",k);
}
return 0;
}
折半查找:又称为二分查找
两个前提条件:1.必须采用顺序存储结构;2.必须按关键字大小有序排列
这就要求对无序的数据进行排序后在输入顺序表中。
【算法思想】:
首先将表 中间位置记录的关键字 与 查找关键字 进行比较,如果相等则查找成功,否则利用中间位置记录将表分为前、后两个子表,如果中间位置记录的关键字大于要查找的关键字,则在前一子表中进一步比较,否则,在后一子表中进行比较。
重复以上过程,直到找到满足条件的记录,此时查找成功,或者直到子表不存在位置,此时查找失败。
例:
折半查找和顺序查找的区别主要就是查找函数的区别以及折半查找前提需要排序,顺序查找需要一个监视哨,其他部分基本相同。
折半查找:
int bin_search(KeyType k,RecordList l)
{
int min,low,high;
low=1;high=l.len;//置初值
while(low折半查找法的优点是比较次数少,查找速度快,平均性能好;缺点是要求待查表为
有序表,且插入删除困难。因此,折半查找适用于不经常变动而查找频繁的有序表。
分块查找
分块查找法要求将链表组织成以下两种索引顺序结构。
1.首先将列表分成若干个块(子表)。一般情况下,块的长度均匀,最后一块可以不满。每块中元素任意排列,即块内无序,但块与块之间有序。
2.构造一个索引表。其中每个索引相对应一个块并记录每块的起始位置以及每块中的最大关键字,索引表按关键字有序排列。
索引存储结构:
存储结点信息时,建立索引表,索引表含有若干个索引项,索引项的一般形式:(关键字,地址),关键字表示一个结点,地址是指向结点的信息。可以通过索引的方法来操作相应位置的数据。
优点:
1.提高数据查找的速度
2.插入、删除时,只需要移动索引表中对应节点的存储地址,而不必移动节点中节点的数据。
缺点:
增加了索引表,所以降低了存储空间的利用率。
【算法思想】
首先将待查关键字与索引表中的最大关键字进行比较,以确定待查记录所在的快 ,运用二分查找到方法。
进一步用顺序查找的方法,在相应块中找到关键字k
typedef struct//索引表
{
int key;//最大关键字
int address;//起始地址
}IdxTable;
typedef IdxTable indxtable[3];//自定义一个IdxTable类型的数组变量
typedef struct//所有节点信息表
{
int key;
}NodeTable;
typedef NodeTable nodetable[18];//自定义一个NodeTable类型的数组变量
int IndxSearch_erfen(indxtable idx,int m,int key1)//二分查找,找到最大关键字
{
int left=0,right=m-1,mid;
while(left<=right)
{
mid=(left+right)/2;
if(idx[mid].key>=key1&&idx[mid-1].keykey1)
right=mid-1;
}
}
//顺序查找
int IndxSearch_shunxu(int n,int m,int key1,indxtable idx,nodetable r)
{//顺序查找,在可能含有待查关键字的块中顺序查找关键字
int b=n/m,i=IndxSearch_erfen(idx,m,key1);/*b表示每块的个数,n表示总数据元素的个数,
m表示分的块数*/
printf("在索引表的起始地址:%d\n",i);
int data_n=i+b;//数据表起始位置到某块终点的长度
while(i=data_n;二是r[i].key==key1
if(i>=data_n)
return -1;
else
return i;
}
**
基于树的查找法
**
1.二叉排序树,又称二叉查找树
定义:或者是一颗空树,或者是具有如下性质的二叉树:
1.若他的左子树不为空,则左子树上节点的值均小于根节点的值。
2.若他的右子树不为空,则右子树上节点的值均大于根节点的值。
3。它的左右子树又分别是二叉排序树。
注意:可以是数值间的大小,可以是ASCII码间的比较。
二叉排序树的存储结构同二叉树,使用二叉链表作为存储结构:
typedef struct node
{
Keytype key;
struct node * lchild,* rchild;
}BSTNode,* BSTree;
2.二叉排序树的插入
将根看成是一个结点,其左右子树又可以看成是颗二叉树,所以,此算法妙在使用递归算法
【算法思想】
若二叉排序树是空树,则key成为二叉排序树的根
若二叉排序树非空,
分三种情况:如果key的值等于节点的值,则停止插入;大于节点的值,则key插入到右子树;小于结点的值,插入到左子树。
void InsertBST(BSTree bst,Keytype key)
{
BSTNode s;
if(bst==NULL)
{
s=(BSTNode *)malloc(sizeof(BSTNode));
s->key=key;
s->lchild==NULL;
s->Rchild==NULL;
bst= &s;//s与bst是两种类型,一个是结构体整型,一个是结构体指针型
}
}
插入时不需要移动元素,不涉及树的整体改动。时间复杂度为O(log2 n)