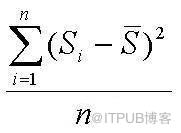Oracle分析函数五——统计分析函数
方差和标准差:
样本中各数据与样本平均数的差的平方和的平均数叫做样本方差;样本方差的算术平方根叫做样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。
数学上一般用E{[X-E(X)]^2}来度量随机变量X与其均值E(X)即期望的偏离程度,称为X的方差。
方差是标准差的平方
方差和标准差。方差和标准差是测算离散趋势最重要、最常用的指标。方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法。标准差为方差的平方根,用S表示。
StdDev返回expr的样本标准偏差。它可用作聚集和分析函数。它与stddev_samp的不同之处在于,当计算的输入数据只有一行时,stddev返回0,而stddev_samp返回null。
Oracle数据库中,标准偏差计算结果与variance用作集聚函数计算结果的平方根相等。该函数参数可取任何数字类型或是任何能隐式转换成数字类型的非数字类型。
STDDEV
功能描述:计算当前行关于组的标准偏离。(Standard Deviation)
SAMPLE:
STDDEV_SAMP
功能描述: 该函数计算累积样本标准偏离,并返回总体变量的平方根,其返回值与VAR_POP函数的平方根相同。(Standard Deviation-Sample)
SAMPLE:
它与stddev_samp的不同之处在于,当计算的输入数据只有一行时,stddev返回0,而stddev_samp返回null。
SELECT
department_id,
first_name||' '||last_name employee_name,
hire_date,
salary,
STDDEV_SAMP(salary) OVER (PARTITION BY department_id ORDER BY hire_date) AS cum_sdev
FROM employees
WHERE department_id in (20,30,60);
STDDEV和STDDEV_SAMP的区别
SELECT
first_name||' '||last_name employee_name,
hire_date,
salary,
STDDEV(salary) OVER (ORDER BY hire_date) "StdDev",
STDDEV_SAMP(salary) OVER (ORDER BY hire_date) AS cum_sdev
FROM employees
VAR_POP
功能描述:(Variance Population)该函数返回非空集合的总体变量(忽略null),VAR_POP进行如下计算:
(SUM(expr2) - SUM(expr)2 / COUNT(expr)) / COUNT(expr)
VAR_SAMP
功能描述:(Variance Sample)该函数返回非空集合的样本变量(忽略null),VAR_POP进行如下计算:
(SUM(expr*expr)-SUM(expr)*SUM(expr)/COUNT(expr))/(COUNT(expr)-1)
SAMPLE:
VARIANCE
功能描述:该函数返回表达式的变量,Oracle计算该变量如下:
如果表达式中行数为1,则返回0
如果表达式中行数大于1,则返回VAR_SAMP
SAMPLE:
SELECT
department_id,
first_name||' '||last_name employee_name,
hire_date,
salary,
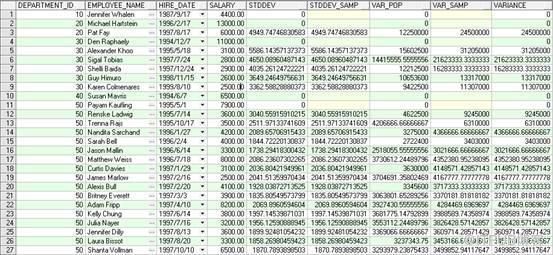
STDDEV(salary) OVER (PARTITION BY department_id ORDER BY hire_date) AS "STDDEV",
STDDEV_SAMP(salary) OVER (PARTITION BY department_id ORDER BY hire_date) AS "STDDEV_SAMP",
VAR_POP(salary) OVER (PARTITION BY department_id ORDER BY hire_date) AS "VAR_POP",
VAR_SAMP(salary) OVER (PARTITION BY department_id ORDER BY hire_date) AS "VAR_SAMP",
VARIANCE(salary) OVER (PARTITION BY department_id ORDER BY hire_date) AS "VARIANCE"
FROM employees
协方差分析是建立在方差分析和回归分析基础之上的一种统计分析方法。
方差分析是从质量因子的角度探讨因素不同水平对实验指标影响的差异。一般说来,质量因子是可以人为控制的。
回归分析是从数量因子的角度出发,通过建立回归方程来研究实验指标与一个(或几个)因子之间的数量关系。但大多数情况下,数量因子是不可以人为加以控制的。
两个不同参数之间的方差就是协方差
若两个随机变量X和Y相互独立,则E[(X-E(X))(Y-E(Y))]=0,因而若上述数学期望不为零,则X和Y必不是相互独立的,亦即它们之间存在着一定的关系。
定义
E[(X-E(X))(Y-E(Y))]称为随机变量X和Y的协方差,记作COV(X,Y),即COV(X,Y)=E[(X-E(X))(Y-E(Y))]。
COVAR_POP
功能描述:返回一对表达式的总体协方差。
SAMPLE:
COVAR_SAMP
功能描述:返回一对表达式的样本协方差
SAMPLE:
SELECT
a.department_id,
a.employee_id,
b.employee_id manager_id,
a.first_name||' '||a.last_name employee_name,
b.first_name||' '||b.last_name manager_name,
a.hire_date,
a.salary employee_salary,
b.salary manager_salary,
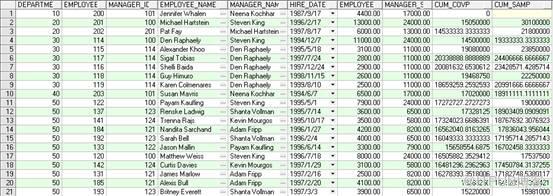
COVAR_POP(a.salary,b.salary) OVER (ORDER BY a.department_id,a.hire_date ) AS CUM_COVP,
COVAR_SAMP(a.salary,b.salary) OVER (ORDER BY a.department_id,a.hire_date ) AS CUM_SAMP
FROM employees a,employees b
WHERE a.manager_id=b.employee_id(+)
CORR
功能描述:返回一对表达式的相关系数,它是如下的缩写:
COVAR_POP(expr1,expr2)/STDDEV_POP(expr1)*STDDEV_POP(expr2))
从统计上讲,相关性是变量之间关联的强度,变量之间的关联意味着在某种程度
上一个变量的值可由其它的值进行预测。通过返回一个-1~1之间的一个数, 相关
系数给出了关联的强度,0表示不相关。
SELECT
a.department_id,
a.first_name||' '||a.last_name employee_name,
b.first_name||' '||b.last_name manager_name,
a.hire_date,
a.salary employee_salary,
b.salary manager_salary,
CORR(a.salary,b.salary) OVER (ORDER BY a.department_id,a.hire_date ) AS CORR
FROM employees a,employees b
WHERE a.manager_id=b.employee_id(+)
image036.jpg
image038.jpg
image040.jpg
image042.jpg
来自 “ ITPUB博客 ” ,链接:http://blog.itpub.net/6517/viewspace-611066/,如需转载,请注明出处,否则将追究法律责任。
转载于:http://blog.itpub.net/6517/viewspace-611066/