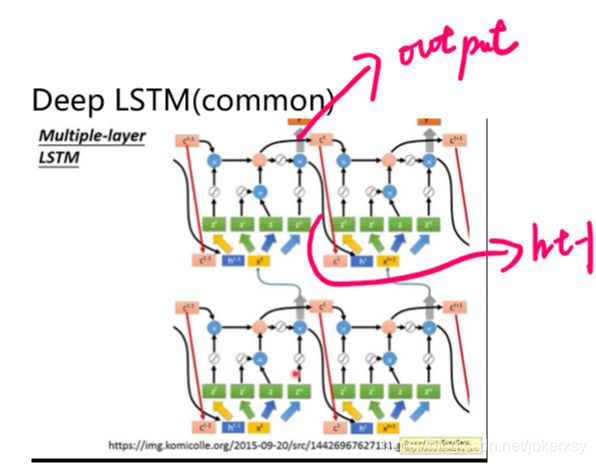
lstm&bilstm输入输出格式(附代码)

Lstm

self.lstm = nn.LSTM(input_size=self.input_size,
                    hidden_size=self.hidden_size,
                    num_layers = self.num_layers,
                    batch_first=True,
                    bidirectional=False,
                    dropout=self.dropout
                    ) 
self.fc1 = nn.Linear(self.hidden_size,int(self.hidden_size/2))
self.fc2 = nn.Linear(int(self.hidden_size/2), 2)

上图中的单向lstm模型的参数分别表示:

• input_size:词向量的维度

• hidden_size:输出层的维度(又称隐藏层，因为上一时间步的输出，会成为下一时间步的参数，如下图)
  

• num_layers:网络的层数

• batch_first:使得原来的 句子的单词数 * batchsize * 词向量维度，转变成batchsize * …

• bidirectional:是否是双向神经网络

• dropout:防止过拟合，一般设0.5，但只有训练集训练时需要dropout,也就是说在验证集、测试集跑模型时。应把dropout置为0

假如我们的输入(input_embeded)的规格如下:

input_embeded:
(batch_size * len_sen(句子长度，也就是句子有多少个单词) * input_size(单词的向量维度)

那经过lstm的输出共有三个，分别为:

output, (h_n, c_n) = self.lstm(input_embeded)

各自的规格分别为

• output:batch_size * len_sen * hidden_size
• h_n: (1*self.num_layers(lstm的层数)) * batch_size * hidden_size
• c_n: (1*self.num_layers) * batch_size * hidden_size

output容易理解，就是所有的输出。假设就一层lstm，那么h_n其实等于output[-1]，也就是说h_n保留的是最后一个时间步的输出，c_n保留的是最后一个时间步的记忆细胞。其中，h_n 是 c_n 经过一个tanh激活函数，在经过一个输出门，得到的。

在情感分类中，我们只需要h_n。并将它继续为给一些全连接层，最后输出，如下面代码所示:

output, (h_n, c_n) = self.lstm(input_embeded)  # h_n:最后一个时间步的输出(1*bi?2:1 * bs * hidden_size)，c_n:最后一层的记忆细胞
out = h_n.squeeze(0)  # 去除第一维
out = F.relu(out)
out_fc1 = self.fc1(out)
out = F.relu(out_fc1)
out_fc2 = self.fc2(out)
return F.log_softmax(out_fc2,dim=-1)

最终输出的规格为: batch_size * 2, 进一步与label进行比较。

BILSTM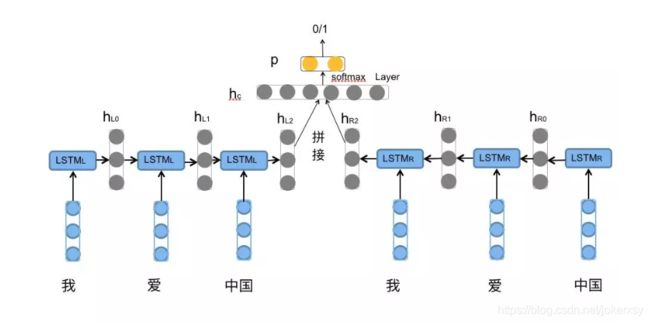

从上面的图可以看出，bilstm与lstm的不同在于，bilstm通过前向、后向，最终得到两个输出，也就是h_n，然后把他们进行拼接，接下去的步骤一样。

BILSTM代码如下

self.lstm = nn.LSTM(input_size=self.input_size,
                    hidden_size=self.hidden_size,
                    num_layers = self.num_layers,
                    batch_first=True,
                    bidirectional=self.bidirectional,
                    dropout=self.dropout
                    ) 
self.fc1 = nn.Linear(self.hidden_size * 2,self.hidden_size)
self.fc2 = nn.Linear(self.hidden_size, 2)                 

假设输入各种跟上面的LSTM一样，看一下输出的格式:
先经过lstm层，输出也是三个，如下:

output, (h_n, c_n) = self.lstm(input_embeded)

现在的h_n的规格为:
(2*self.num_layers(lstm的层数)) * batch_size * hidden_size

我们需要对h_n进行一开始的图中所示的拼接:

out = torch.cat([h_n[-1, :, :], h_n[-2, :, :]], dim=-1)

这一步得到的out的规格为:
bs * （2*hidden_size）

得到out，进一步经过一下全连接层，然后输出，代码如下:

out = F.relu(out)
out_fc1 = self.fc1(out)
out = F.relu(out_fc1)
out_fc2 = self.fc2(out)