2020-5-9模拟赛题解
前言
6 : 30 6:30 6:30 开考,我大概 8 : 00 8:00 8:00 把这套题拍好,充分吸取 NOI Online \texttt{NOI Online} NOI Online 的教训,所以每题都拍上了。
正文
T1
题目描述
在一个网格图中,每次可以从 ( x , y ) (x,y) (x,y)
- 向上移动到 ( x − 1 , y ) (x-1,y) (x−1,y);
- 向下移动到 ( x + 1 , y ) (x+1,y) (x+1,y)
- 向左移动到 ( x , y − 1 ) (x,y-1) (x,y−1)
- 向右移动到 ( x , y + 1 ) (x,y+1) (x,y+1)
求从 0 , 0 0,0 0,0 点出发,依此经过 ( x 1 , y 1 ) ∼ ( x n , y n ) (x_1,y_1)\sim (x_n,y_n) (x1,y1)∼(xn,yn) 的最短距离
分析
网格图中的最短距离 = = = 曼哈顿距离
曼哈顿距离 = = = 行的绝对值 + + + 列的绝对值
代码:
#include T2
题目描述
给出 n n n 个人的名字和他们的 Rating \texttt{Rating} Rating,求这 n n n 个人的排名(第 i i i 个人的排名定义为 Rating \texttt{Rating} Rating 比第 i i i 个人高的人数 + 1 +1 +1)
分析
这题的答案跟名字没有关系,而且数据范围很小。
这样的话,我们怎么做都可以。
我的话是对这个数组进行排序,然后暴力查找这个最早出现在第几个(因为排名 = = = Rating \texttt{Rating} Rating 比他高的人数 + + + 1 1 1)
代码
#include T3
题目描述
有 4 4 4 个人 A,B,C,D \texttt{A,B,C,D} A,B,C,D,每个人有一个实力值。分别为 a , b , c , d a,b,c,d a,b,c,d
你现在要把他们分成两个队伍,要求每个队伍里都得有人,并且使两队实力值之和的差最小。
分析
这题直接暴力找出所有方法就好了。
并没有什么技巧。
代码
#include T4
题目描述
一个序列,你可以用一个单位的时间从头部或尾部拿走一个数字,并得到这个数的值。你拿走这个数后,其他没有被拿走的数字就会全部 − 1 -1 −1。
分析
这题的话很显然有一个结论,那就是吃的顺序不会影响到答案。
这样就简单了,我们求遍和,再把该减的减去就行了。
代码
#include T5
题目描述
子序列的定义:序列 a \texttt{a} a 是 b \texttt{b} b 的子序列,当且仅当从 b \texttt{b} b 中删除若干个元素能得到 a \texttt{a} a。
小 R \texttt{R} R 有两个序列 a \texttt{a} a, b \texttt{b} b,
要求你找到一个最长的序列c,满足以下条件中的任何一个:
c是a的子序列但不是b的子序列;
c是b的子序列但不是a的子序列;
因为出题人不会写
spj,所以就只要你输出c的最长长度即可.
如果找不到,就输出0.
分析
这题其实并不复杂。
- 如果两个序列不完全相同,显然答案 = = = max { \max\{ max{ 第 1 1 1 个序列的长度,第 2 2 2 个序列的长度 } \} }
- 如果两个序列完全相同,答案自然是 0 0 0。
代码
#include T6
题目描述
有 n n n 个石头,第 i i i 个石头的坐标为 a i a_i ai,不保证 a i a_i ai 有序。
你只能往前跳,并且你必须从 0 0 0 开始,中途踩到所有的石头并最后跳到坐标为m的位置。
你有一个能力值 G G G, G G G 不是定值在一次跳跃中不会变化,但在一次跳跃中你每次能跳跃的距离不能大于你的能力值 G G G。
有时候你可能跳不到石头上,这时候你就会落到河里.安全起见,你只能落水不超过 k k k 次。
求出为了使落水不超过 k k k 次,你至少需要的能力值。
分析
这个直接二分 G G G,看落水次数是否 ≤ k \leq k ≤k 就行了。
代码
#include T7
题目描述
有一个长为 n n n 的序列 a 1 , a 2 , ∼ , a n a_1,a_2,\sim,a_n a1,a2,∼,an。
记 s ( L , R ) = max { a [ L ] , a [ L + 1 ] , . . . . . , a [ R ] } − min { a [ L ] , a [ L + 1 ] , . . . a [ R ] } ( L ≤ R ) s(L,R) = \max\{a[L],a[L+1],.....,a[R]\}-\min\{a[L],a[L+1],...a[R]\} (L\leq R) s(L,R)=max{ a[L],a[L+1],.....,a[R]}−min{ a[L],a[L+1],...a[R]}(L≤R),即 s ( L , R ) s(L,R) s(L,R) 为序列中第 L L L 个数到第 R R R 个数的最大值和最小值之差。
求出对于所有的满足 1 ≤ L ≤ R ≤ n 1\leq L\leq R\leq n 1≤L≤R≤n 的 L , R L,R L,R 的 s ( L , R ) s(L,R) s(L,R) 之和。
分析
RMQ \texttt{RMQ} RMQ 万岁!智商不够,数据结构来凑。
我的这种做法很不要动脑子,我暂时很没找到别的做法。
RMQ \texttt{RMQ} RMQ 算法
简单讲讲 RMQ \texttt{RMQ} RMQ
RMQ \texttt{RMQ} RMQ 又称 ST \texttt{ST} ST 表,可以实现 O ( 1 ) O(1) O(1) 静态区间查询最大或最小值,线段树的话会多一个 log \log log。并且这种算法初始化的时间复杂度也是非常优秀的—— n log 2 n n\log_2 n nlog2n。
这个东西如何实现呢?这个东西本质上就是一个倍增。
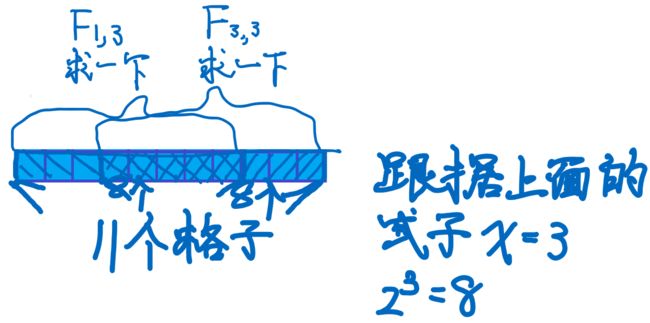
定义 F i , j F_{i,j} Fi,j 表示第 i ∼ i + 2 j i\sim i+2^{j} i∼i+2j 个数中最小的。
学过倍增的同学,这个递推式应该很简单就能推出来。
重点讲查找,其实上面的内容可能不足为奇,但是查找这部分确实有技术含量了。
首先,设一个数为 2 x 2^x 2x
对于任意数,一定可以找到 x x x 满足以下条件:
- 2 x ≤ 2^x \leq 2x≤ 这个数
- 2 x × 2 ≥ 2^x\times 2 \geq 2x×2≥ 这个数
没有理解也没关系,我们来看这个算法到达是怎么实现的
这个图应该还是满直观的
代码
#include T8
题目描述
有一个长为 n n n 的序列 a 1 ∼ a n a_1 \sim a_n a1∼an,保证序列里的数字都是 0 0 0 或 1 1 1。
记 z ( x ) z(x) z(x) 为关于整数 x x x 的函数。
- 当 x x x 为奇数时 z ( x ) = 1 z(x) = 1 z(x)=1;
- 当 x x x 为偶数时 z ( x ) = 0 z(x) = 0 z(x)=0。
记 f ( L , R ) = z ( a [ L ] + a [ L + 1 ] + . . . + a [ R ] ) f(L,R) = z(a[L]+a[L+1]+...+a[R]) f(L,R)=z(a[L]+a[L+1]+...+a[R])。
记 s ( L , R ) = z s(L,R) = z s(L,R)=z(所有满足 L ≤ i ≤ j ≤ R L\leq i\leq j\leq R L≤i≤j≤R 的 f ( i , j ) f(i,j) f(i,j) 之和)
有 q q q 次询问,每次给你一个 L , R L,R L,R,要你求出 s ( L , R ) s(L,R) s(L,R) 的值。
分析
找规律
这道题我们先不要管 m o d 2 \bmod\ 2 mod 2。
我们先来看看 1 ∼ n 1\sim n 1∼n 中每个数在所有 1 ≤ L ≤ R ≤ n 1\leq L\leq R\leq n 1≤L≤R≤n 中 L ∼ R L\sim R L∼R 的区间中被计算了多少次。(本来其实是希望用差分序列找通项式的,结果有意外的惊喜)
先来写个程序
#include 我们来试试不同 n n n 的值会对计算次数产生什么影响。
- 当 n n n = = = 1 1 1 时,程序中的 a a a 序列为
1; - 当 n n n = = = 2 2 2 时,程序中的 a a a 序列为
2 2; - 当 n n n = = = 3 3 3 时,程序中的 a a a 序列为
3 4 3; - 当 n n n = = = 4 4 4 时,程序中的 a a a 序列为
4 6 6 4; - 当 n n n = = = 5 5 5 时,程序中的 a a a 序列为
5 8 9 8 5; - 当 n n n = = = 6 6 6 时,程序中的 a a a 序列为
6 10 12 12 10 6; - 当 n n n = = = 7 7 7 时,程序中的 a a a 序列为
7 12 15 16 15 12 7。
这个时候我们再来关注一下 m o d 2 \bmod 2 mod2 的余数
- 当 n n n = = = 1 1 1 时,程序中的 a a a 序列为
1; - 当 n n n = = = 2 2 2 时,程序中的 a a a 序列为
0 0; - 当 n n n = = = 3 3 3 时,程序中的 a a a 序列为
1 0 1; - 当 n n n = = = 4 4 4 时,程序中的 a a a 序列为
0 0 0 0; - 当 n n n = = = 5 5 5 时,程序中的 a a a 序列为
1 0 1 0 1; - 当 n n n = = = 6 6 6 时,程序中的 a a a 序列为
0 0 0 0 0 0; - 当 n n n = = = 7 7 7 时,程序中的 a a a 序列为
1 0 1 0 1 0 1。
规律已经很明显了
- 当 n n n 为偶数的时候,全部都为 0 0 0;
- 当 n n n 为奇数的时候,一个 0 0 0 一个 1 1 1 间隔开来的。
所以
- 当询问区间长度为偶数时,直接输出 0 0 0;
- 当询问区间长度为奇数是,答案为 a L , a L + 2 , a L + 4 … a R a_L,a_{L+2},a_{L+4} \ldots a_{R} aL,aL+2,aL+4…aR
前缀和
如何求出 a L , a L + 2 , a L + 4 … a R a_L,a_{L+2},a_{L+4} \ldots a_{R} aL,aL+2,aL+4…aR 呢?
我们可以用上前缀和。
我们这样求出
for(int i=1;i<=n;i++)s[i]=s[i-2]+a[i];//似乎RE一点点没关系
这样就好办了,我们直接去解决询问了。
while(T--){
int l,r;
read(l);read(r);
if((r-l+1)%2==0)puts("0");//区间的长度为偶数
else{
int ans=(s[r]-s[l-2])%2;
printf("%d\n",ans);
}
}
代码
#include 后记
这场比赛也正是检查的好,只有有这个习惯,才能保证该有的分数能全部拿到。
到目前为止,还有一点点的遗憾, T 8 T8 T8 我确乎不会对那个规律进行证明,继续思考吧!