ZJ_Improve

Coursera | Andrew Ng (01-week-4-4.2)—前向和反向传播

该系列仅在原课程基础上部分知识点添加个人学习笔记，或相关推导补充等。如有错误，还请批评指教。在学习了 Andrew Ng 课程的基础上，为了更方便的查阅复习，将其整理成文字。因本人一直在学习英语，所以该系列以英文为主，同时也建议读者以英文为主，中文辅助，以便后期进阶时，为学习相关领域的学术论文做铺垫。- ZJ

Coursera 课程 |deeplearning.ai |网易云课堂

转载请注明作者和出处：ZJ 微信公众号-「SelfImprovementLab」

知乎：https://zhuanlan.zhihu.com/c_147249273

CSDN：http://blog.csdn.net/JUNJUN_ZHAO/article/details/79015964

4.2 Forward and Backward Propagation (前向和反向传播)

(字幕来源：网易云课堂)

In a previous video you saw the basic blocks of implementing a deep neural network,a forward propagation step for each layer,and a corresponding backward propagation step.let’s see how you can actually implement these steps.we’ll start at forward propagation,recall that what this will do is input a[l−1] ,and output a[l] and the cache z[l] ,and we just said that from implementational point of view,maybe we’ll cache w[l] and b[l] as well,just to make the function call easier in different exercises,and so the equations for this should already look familiar,the way to improve the forward function is just,this equals w[l] x a[l−1] plus b[l] ,and then al equals the activation function applied to z,and if you want a vectorized implementation,then it’s just that times A l minus 1 plus b,where the b being python broadcasting,and A[l] equals g applied element wise to Z[l] ,and you’ll remember on the diagram for the forth step,where we have this chain of boxes going forward.

在之前的视频你看过了，构成深度神经网络的基本模块，比如每一层都有的前向传播步骤，以及一个相对的反向传播步骤，现在我们来看看如何实现这些步骤，我们从前向传播开始，回忆一下这里的符号表示输入 a[l−1] ，输出是 a[l] 缓存是 z[l] ，我们就可以从实现的角度来说，可能也可以缓存一下 w[l] 和 b[l] ，这样就可以更容易地在不同的练习中调用函数，那么这些等式应该看起来比较熟悉了，更新前向函数的方法是， z[l] 等于 w[l] 乘以 a[l−1] 加 b[l] ，然后 a[l] 等于作用于 z 的激活函数，如果你想要向量化的实现过程，那就是 Z[l] 等于 W[l] 乘以 A[l−1] 加 b，其中 b 是 python 广播， A[l] 等于 g 作用于 Z[l] 的每一个元素，你应该还记得在图中的第四步，也就是我们有这一系列往前走的小盒子。

重点：

构成深度神经网络的基本模块：每一层都有前向传播的步骤，以及一个相对的反向传播步骤。

Forward Propogation for layer l :

Input:a[l−1] # a 符号代表激活函数层，当 l = 1 时，则 a[0] 为特征 x

Output:a[l],cache(z[l]),w[l],z[l]

对比看：( z=wTx+b )

z[l]=w[l]a[l−1]+b[l]

对比看：（ a=σ（z））

a[l]=g[l](z[l])

Vectorized 将以上向量化：

Z[l]=W[l]A[l−1]+b[l]

A[l]=g[l](Z[l])

so you initialize that with feeding in A[0] , which is equal to X,so you initialize this really was the input to the first one right,it’s really a0 which is,the input features to either for one training example,if you’re doing one example at a time or um, A[0] the entire training so if you are processing the entire training set,so that’s the input to the first forward function in the chain,and then just repeating this allows you,to compute forward propagation from left to right.

需要给入 A[0] 也就是 X 来初始化，初始化是第一层的输入值对吧， a[0] 就是对于一个训练样本的输入特征，如果你每一次只做一个样本或者，如果针对一整个训练集的话输入特征就是 A[0] ，所以这就是这条链的第一个前向函数的输入，重复这个步骤，就能从左到右计算前向传播。

重点：

a[0] ：是对于一个训练样本的输入特征。

A[0] ：是针对一整个训练集的话输入特征。

next let’s talk about the backward propagation step,here you go is the input dA[l] and output da[l−1] and dW[l] & db[l] ,let me just write out the steps you need to compute these things, dz[l] is equal to dA[l] element-wise product with g[l] ’ (z[l]), and then compute the derivatives dW[l] equals dz[l] times a[l−1] .I didn’t explicitly put that in the cache,where it turns out you need this as well,and then db[l] is equal to dz[l] ,and finally da[l−1] there’s equal to W[l] transpose times dz[l] ,ok and I don’t want to go through the detailed derivation for this,but it turns out that,if you take this definition to da and plug it in here,then you get the same formula as we had in there previously,for how you compute dz[l] as a function of the previous dz l,in fact well if I just plug that in here you end up that dz[l] is equal to W[l+1] transpose dz[l+1] times g[l] ’ (z[l]) .I know this is a looks like a lot of algebra and,you can actually double check for yourself that this is the equation,where I’ve written down for back propagation last week,when we were doing in your network with just a single hidden layer,and as you reminder this times this element-wise product,but so all you need is,those four equations to implement your backward function.

下面我们讲一下反向传播的步骤，这里的输入是 dA[l] 输出是 da[l−1] dW[l] 和 db[l] ，我在这会写下来计算所需要的步骤， dz[l] 等于 dA[l] 对应相乘 g[l] ’ (z[l]) 的每一个元素，然后求导 dW[l] 等于 dz[l] 乘以 a[l−1] 。我没有特别把这一步放进缓存，但之后可能会需要， db[l] 等于 dz[l] ，最后 da[l−1] 等于 W[l] 的转置阵乘以 dz[l] ，我省略了求导过程的很多细节，但是最后的结果是，如果你把 da 的定义代入这个式子，那么你会得到一个和之前一样的式子，也就是用来计算前一个 dz[l] 函数的 dz[l] ，实际上如果我只把它代入到会得到 dz[l] ，等于 W[l+1] 的转置阵 dz[l+1] 乘以 g[l]′(z[l]) ，我知道这里有很多代数运算，你可以自己确认一下这就是之前，我在上周曾经写过的反向传播的等式，我们之前建的是单隐层网络，提醒一下大家这里（*）是逐个元素相乘，但是你依然只需要，这 4 个等式来实现反向函数。

重点：

反向传播（Backward propagation）

Input：da[l]

Output：da[l−1]，dW[l]，db[l]

公式：

dz[l]=da[l]∗g[l]′(z[l])dW[l]=dz[l]⋅a[l−1]db[l]=dz[l]da[l−1]=W[l]T⋅dz[l]

da[l−1]代入dz[l] ，有：

dz[l]=W[l+1]T⋅dz[l+1]∗g[l]′(z[l]) d z [ l ] = W [ l + 1 ] T ⋅ d z [ l + 1 ] ∗ g [ l ] ′ ( z [ l ] )

and then finally I’ll just write out the vectorized version,so the first line becomes dz[l] ,equals dA[l] element-wise product with g[l]′(z[l]) ,may be no surprise there, dW[l] becomes 1 over m dz[l] times A[l−1] transpose,and then db[l] becomes one over m,np dot sum dz[l] then axis is equal to one keepdims equals true,we talked about the use of,np dot sum in the previous week to compute db,and then finally da[l−1] is W[l] transpose times dz[l] ,so this allows you to input this quantity da over here,and output on dW[l] db[l] ,the derivatives you need as well as da[l−1] right as follows,so that’s how you implement the backward function.

最后我会写出来这个向量化的版本，那第一行是 dz[l] ，等于 dA[l] 乘以对应元素的 g[l] ’ (z[l]) ，这应该还挺明显的， dW[l] 等于 1/m 乘以 dz[l] 再乘以 A[l−1] 的转置阵， db[l] 等于 1/m，乘以 np.sum(dz[l], axis=1, keepdims=True)，我们在上周讨论过，用来计算 db 的 np.sum 的用法，最后 da[l−1] 等于 W[l] 的转置阵乘以 dz[l] ，这可以用来作为 da 的输入值，以及 dW[l] 和 db[l] 的输出值，以及一些需要求的导数还有 da[l−1] ，所以这就是实现反向函数的方法。

重点：

向量化：

dZ[l]=dA[l]∗g[l]′(Z[l])dW[l]=1mdZ[l]⋅A[l−1]db[l]=1mnp.sum(dZ[l],axis=1,keepdims=True)dA[l−1]=W[l]T⋅dZ[l] d Z [ l ] = d A [ l ] ∗ g [ l ] ′ ( Z [ l ] ) d W [ l ] = 1 m d Z [ l ] ⋅ A [ l − 1 ] d b [ l ] = 1 m n p . s u m ( d Z [ l ] , a x i s = 1 , k e e p d i m s = T r u e ) d A [ l − 1 ] = W [ l ] T ⋅ d Z [ l ]

上面这部分可以结合 Coursera | Andrew Ng (01-week-3-3.9)—神经网络的梯度下降法以及 Coursera | Andrew Ng (01-week-3-3.10)—直观理解反向传播回忆一下中间省略的求导过程。

大致提一下：

a=σ(z)=11+e−z

σ(z)′=a(1−a)

又因为 da=−ya+(1−y)1−a

且 dz=dLda⋅dadz=da⋅g(z)′

剩下的再根据上面两个链接去推导就可以了。

反向传播辅助理解：已知输入 da[l] , 最终要求得的是 da[l−1] ，但是中间需要先求出 dz[l] ,然后才可以得出 dw[l] , db[l] ,最终求得 da[l−1]

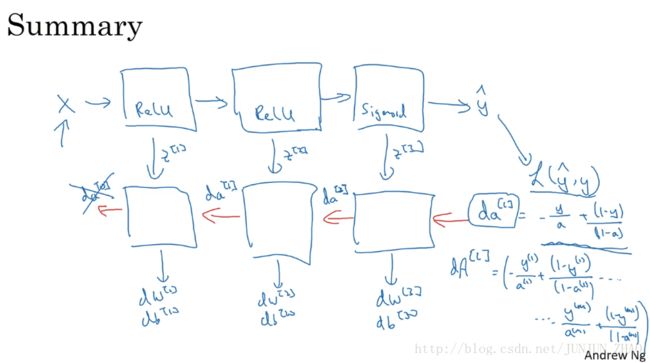
so just to summarize um take the input x,you might have the first layer maybe has a ReLU activation function,then go to the second layer maybe uses,another ReLU activation function,goes to the third layer maybe has a sigmoid activation function.if you’re doing binary classification and this outputs y hat,and then using Y hat you can compute the loss,and this allows you to start your backward iteration.I draw the arrows first I guess I don’t have to change pens too much,where you we’ll then have back prop compute the derivatives,compute your dw[3] db[3] dw^{[2]} db[2] dw[1] db[1] ,and along the way you would be computing.I guess the cache will transfer z[1] z[2] z[3] ,and here are you pass backward da[2] and da[1] ,this could compute da[0] but we won’t use that,so you can just discard that,and so this is how you implement,forward prop and back prop for a three-layer your network,now there’s just one last detail delight didn’t talk about,which is for the forward recursion.

最后小结一下用 x 作为输入，第一层你可能会有一个修正线性单元激活函数，然后第二层可能会用，另一个修正线性单元激活函数，到第三层可能是 sigmoid 函数。如果你想做二分分类输出值是 y^ ，用 y^ 你可以计算出损失，这样你就可以开始向后迭代，我先画把箭头全画好这样就不用经常换笔啦，接下来你就可以用反向传播求导，用来求 dw[3] db[3] dw[2] db[2] dw[1] db[1] ，在这途中你会计算，缓存会把 z[1] z[2] z[3] 传递过来，然后这里回传 da[2] 和 da[1] ，可以用来计算 da[0] 但是我们不会直接用，你可以直接抛弃，好啦现在讲完了一个三层网络的，前向和反向传播，现在就只剩下最后一点细节我还没讲，就是前向递归。

we would initialize it with the input data x,how about the backward recursion,well it turns out that um da of l when you’re using logistic regression,when you’re doing binary classification is equal to,y over a plus 1 minus y over 1 minus a,so it turns out that the derivative of,the loss function respect to the output,with respect of y hat can be shown to be equal to this,if you’re familiar with calculus if you look up the loss function L,and take derivatives respect to y hat with respect to a,you can show that you get that formula,so this is the formula you should use,for da for the final layer capital L,and of course if you were to have a vectorized implementation,then you initialize the backward recursion,not with this but with da capital A for the layer l,which is going to be you know the same thing for the different examples y over a,for the first training example plus 1 minus y for the first training example over 1 minus a,for the first training example dot dot dot down to the training example 1 minus a of M,so that’s how you ought to implement the vectorized version.

我们会用输入数据 x 来初始化，那么反向递归呢，当你用 Logistic 回归，做二分分类的时候 dA[l] ，等于 −ya+(1−y)1−a ，然后相对于 y^ 的，损失函数的导数，可以被证明等于 dA[l] 的这个式子，如果你对微积分很熟悉可以再研究一下损失函数 L，对 y^ 和a求导，你就可以证明你能得到这个公式，这个 da 的公式应该用在 L，也就是用在最后一层上，当然了如果你想要向量化这个实现过程，那就需要初始化反向递归，那就不能用这个公式而应该用 dA[l] 的公式，不一样的情况，但是同样的道理 -y/a，在第一个训练样本中， dA[l] 就是 −ya+(1−y)1−a ，从第一个例子一直到，第 m 个训练样本，这就实现向量化版本的方式。

that’s how you initialize,the vectorized version of backward propagation,so you’ve now seen,the basic building blocks of both forward prop as well as back prop,now if you implement these equations,you will get a correct implementation of forward prop and back prop,to get to the derivatives you need,you might be thinking well there’s a lot equations.I’m slightly confused I’m not quite sure I see how this works,and if you’re feeling that way my advice is,when you get to this week’s programming assignment,you will be able to implement these for yourself,and there’ll be much more concrete,and I know there’s a lot of equations,and maybe some equations doesn’t make complete sense,but if you work through the calculus and the linear algebra,which is not easy so you know feel free to try,but that’s actually one of,the more difficult derivations in machine learning.

换句话说就是，初始一个向量化反向传播的方法，目前为止你已经看过了，前向和反向传播的一些基石，如果你现在去尝试实现这些式子，你会得到一个正确实现的前向和反向传播，来得到你所需要算的导数，你可能在吐槽这也太多公式了吧，可能懵了没搞懂这都是咋回事，要是你这么觉得我给你个建议，就是当你开始这周的编程作业时，你需要亲自实现这一切，那时候就会学的更加扎实，我知道这里有好多式子，你不需要弄到所有式子，但是如果你稍微补补微积分和线性代数，虽然并不容易但是还是要试试，况且这还是机器学习里面，相对比较难的推导了。

It turns out the equations wrote down,are just the calculus equations for,computing the derivatives especially in back prop,a bit abstract a little bit mysterious to you,my advice is when you’ve done the problem exercise,it will feel a bit more concrete to you,although I have to say you know even today,when I implement a learning algorithm,sometimes even I’m surprised,when my learning algorithm implementation works,and it’s because lot of complexity of machine learning,comes from the data,rather than from the lines of code,so sometimes you feel like,you implement a few lines of code not quite sure what it did,but it almost magically work,and it’s because of all the magic is,actually not in the piece of code you write,which is often you know not too long it’s not it’s not exactly simple,but there’s not you know 10,000 100,000 lines of code,but you feed it so much data that sometimes,even though I work the machine learning for a long time,sometimes it’s so you know surprises me a bit,when my learning algorithm works.

所以其实刚刚讲的那些式子，都不过是用来在反向传播中，求导的微积分公式，不过我要再强调一下，如果它们看起来很是抽象有点神秘，我的建议还是做做作业，做完就会觉得神清气爽，虽然我必须要说，到现在我在实现一个算法的时候，有时候我也会惊讶，怎么莫名其妙就成功了，那是因为机器学习里的复杂性，是来源于数据本身，而不是一行行的代码，所有有时候你会感觉，你实现了几行代码但是不太确定它具体做了什么，但是奇迹般地实现了，那是其实不是，因为真正神奇的东西不是你写的程序，通常情况下你的代码段不会很长虽然也不会太简单，但是不会需要写一万或者十万行代码，但有时当你喂入超多数据之后，就算我已经搞机器学习这么长时间了，有时候也还是在算法管用的时候，惊讶一下下。

because lots of complexity of your learning algorithm comes from the data rather than necessarily from your writing,you know thousands and thousands of lines of code,all right so that’s um how do you implement deep neural networks,and again this will become more concrete,when you’ve done the programming exercise,before moving on I want to discuss in the next video,want to discuss hyper parameters and parameters,it turns out that when you’re training deep nets,being able to organize your hyper params well,will help you be more efficient in developing your networks.In the next video let’s talk about exactly what that means.

因为实际上你的算法的复杂性，来源于数据而不是你写的代码，因为你不需要写个几千行的代码，好这节课就讲了怎么实现深度神经网络，再重申一下这些知识点会，在做完编程作业之后得到巩固，在继续下一课之前我想说一下，之后我们会讨论超参数和参数，其实当你训练深度网络时，能够好好安排超参数，会帮助你提高开发网络的效率，在下个视频中我们会谈谈具体的原因。

重点总结：