中国剩余定理与扩展中国剩余定理

中国剩余定理又名孙子定理

用来求解同余线性方程组
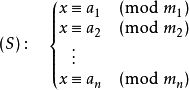其中m1,m2,m3…两两互质，求x的最小整数解；

设M为m1,m2,m3…的公倍数。


根据上面的推导，为什么x的通解形式是累加呢？

根据上面推导，推导出x的解，接下来就可以开始写题了。
https://www.luogu.org/problemnew/show/P3868 一道模板题

附上完整代码

#include
using namespace std;
#define ll long long int
#define fin(a,n) for(int i=a;i<=n;i++)
const int maxn=20;
ll a1[20],b1[20];
ll mul(ll a,ll b,ll mod)//求（a*b）%mod ，防止a*b炸ll 
{
 ll ans=0;
 while(b>0)
 {
 if(b&1)ans=(ans+a)%mod;//如果b对答案有贡献 
 a=(a+a)%mod;
 b>>=1;
    }
    return ans;
}
ll exgcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得 
{
 if(b==0)
 {
  x=1;
  y=0;
  return a;
 }
 ll ans=exgcd(b,a%b,x,y);
 ll temp=x;
 x=y;
 y=temp-(a/b)*y;
 return ans;
}
ll china(int n)//中国剩余定理 
{
 ll M=1,ans=0,x,y;
 fin(1,n)M*=b1[i]; 
 fin(1,n)
 {
  ll a,b;
  a=M/b1[i];//此处的按照ax+by=1的形式，因为互素所以等号右边恒为1.
  b=b1[i];
  exgcd(a,b,x,y);
  x=(x%b+b)%b;//求出最小的x 
     ans=(ans+mul(mul(a,x,M),a1[i],M))%M;//此处对应求和即ai*xi*mi 
 }
 return (ans+M)%M;
}
int main()
{
 int n;
 scanf("%d",&n);
 fin(1,n)scanf("%lld",&a1[i]);
 fin(1,n)scanf("%lld",&b1[i]);
 fin(1,n)a1[i]=(a1[i]%b1[i]+b1[i])%b1[i];//预处理数据 
 ll tans=china(n);
 printf("%lld",tans);
}

孙子定理，证毕

扩展中国剩余定理，相同的方程

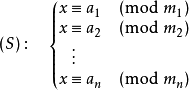
但此处，m1,m2….两两不互质
这时怎么推解呢？如下图

看到上述方程是不是就明白了？我们可以根据递推，把通解带进下一个方程，看看有没有解，不就是整个方程有没有解吗？
上面的方程只有k一个未知数，用扩展欧几里得求出最小的k 值，然后再把答案更新一遍，不断的往下推。大功告成！
给两道模板题
https://www.luogu.org/problemnew/show/P4777
https://cn.vjudge.net/problem/POJ-2891
两道都是模板题，区别在于POJ上的需要多组数据输出。
附上完整代码

#include
#include
using namespace std;
#define fin(a,n) for(int i=a;i<=n;i++)
#define ll long long int
const int maxn=2e5+10;
ll a[maxn],b[maxn];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
	if(b==0)
	{
	x=1;
	y=0;
	return a;
	}
	ll gcd=exgcd(b,a%b,x,y);
	ll temp=x;
	x=y;
	y=temp-a/b*y;
	return gcd;
}
ll mul(ll a,ll b,ll mod)//快速乘法
{   ll res=0;
    while(b>0)
    {
	if(b&1)res=(res+a)%mod;
	a=(a+a)%mod;
	b>>=1;
   }
   return res;
}
ll gcd(ll a,ll b)
{
	return b?gcd(b,a%b):a;
}
ll exchi(int k)
{
   ll a0,b0;
   a0=a[1];
   b0=b[1];
   fin(2,k)
   {
   	ll a1=a[i],b1=b[i];
   	ll gd=gcd(a1,a0);//gcd 
   	if((b1-b0)%gd!=0)return -1;//b0表示之前方程的答案，此处b1-b0表示方程的右边 
   	ll x,y;
   	exgcd(a0,a1,x,y);//a0为累乘的最小公倍数，a1为当前的模值 
   	x*=(b1-b0)/gd;//根据扩展欧几里得，出来的结果是ax+by=gcd的值，所以缩小之后需要放大 
   	a1*=a0/gd;//a1表示最小公倍数 
   	b0=(mul(x,a0,a1)+b0)%a1;//把答案最小化 mul中表示x*a0%a1；
   	a0=a1;//代换递推 
   }
   return (b0%a0+a0)%a0;//最小化答案 
}
int main()
{   int n; 
	while(~scanf("%d",&n))
	{
	fin(1,n)scanf("%lld %lld",&a[i],&b[i]);
	ll tans=exchi(n);
	printf("%lld\n",tans);
    }
	
}