LeetCode 第34场夜喵双周赛 题解
这次偏简单 但是还是有挺多细节的
文章目录
- a.矩阵对角线元素的和
-
- a.题目
- a.分析
- a.参考代码
- b.分割字符串的方案数
-
- b.题目
- b.分析
- b.参考代码
- c.删除最短的子数组使剩余数组有序
-
- c.题目
- c.分析
- c.参考代码
- d.统计所有可行路径
-
- d.题目
- d.分析
- d.参考代码
a.矩阵对角线元素的和
a.题目
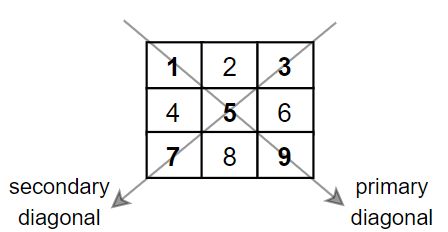
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
输入:mat = [[1,2,3],
[4,5,6],
[7,8,9]]
输出:25
解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25
请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2
输入:mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]
输出:8
示例 3
输入:mat = [[5]]
输出:5
提示
- n == mat.length == mat[i].length
- 1 <= n <= 100
- 1 <= mat[i][j] <= 100
a.分析
第一题嘛 拼手速 用脑子的最好都不要用
题目说明重叠的不算 那么赛后分析得知 只有奇数方阵的[i,i]中心会重叠
比赛时候就直接开一个vis记录是否访问过 然后无脑两条对角线计数就是了
一条从(0,0)开始到(n-1,n-1) 一条从(0,n-1)到(n-1,0)
时间复杂度为O(n) 即对角线的长度
a.参考代码
class Solution {
public:
int vis[105][105]={
0}; //强行无脑记录
int diagonalSum(vector<vector<int>>& mat) {
int n=mat.size();
int m=mat[0].size(); //比赛时候甚至没看是否是方阵
int ans=0;
int x=0,y=0,a=0,b=m-1;
while(x<n&&y<m){
//对角线长度肯定一样过的
ans+=mat[x][y];
vis[x][y]=true;
x++;
y++;
if(!vis[a][b])ans+=mat[a][b]; //重叠了
vis[a][b]=true;
a++;
b--;
}
return ans;
}
};
b.分割字符串的方案数
b.题目
给你一个二进制串 s (一个只包含 0 和 1 的字符串),我们可以将 s 分割成 3 个 非空 字符串 s1, s2, s3 (s1 + s2 + s3 = s)。
请你返回分割 s 的方案数,满足 s1,s2 和 s3 中字符 ‘1’ 的数目相同。
由于答案可能很大,请将它对 10^9 + 7 取余后返回。
示例 1
输入:s = “10101”
输出:4
解释:总共有 4 种方法将 s 分割成含有 ‘1’ 数目相同的三个子字符串。
“1|010|1”
“1|01|01”
“10|10|1”
“10|1|01”
示例 2
输入:s = “1001”
输出:0
示例 3
输入:s = “0000”
输出:3
解释:总共有 3 种分割 s 的方法。
“0|0|00”
“0|00|0”
“00|0|0”
示例 4
输入:s = “100100010100110”
输出:12
提示
- s[i] == ‘0’ 或者 s[i] == ‘1’
- 3 <= s.length <= 10^5
b.分析
对于区间和 第一时间就要用前缀和把其预处理掉 方便以O(1)获取区间和
题目说是分割成三个位置 那么起码得枚举两个分割点 但是再一看数据量
O(n^2)的肯定是过不去的 因此直觉告诉我要枚举其中一个分割点然后二分找另一个分割点 (直觉O(nlogn)能做 不一定最优)
既然确定了要枚举一个分割点i 那么第一部分one的1的和就为sum[i]
然后我们是可以知道全部总和是为sum[n-1]的 那么第二部分two和第三部分three的总和我们可以通过sum[n-1]-sum[i]得出
显然 如果想要 one=two=three 那么现在必须要one==(three+two)/2
因此我们直接就可以知道第二个分割点在哪 又因为sum是非递减的 所以可以在后半部分用二分找到所有 sum[i]==one×2 的值
我们仅需要找到连续的one×2的区间是什么即可 因此可以用lower_bound和upper_bound把上下界给找出来
因此我们就得到了 固定某个第一分割点后得到的可行的第二分割点的 的数量了
因此我们只需要不断去枚举第一个分割点即可 总的复杂度为O(nlogn)
赛后考虑优化:
显然对于总和为固定sum[i-1]的数组 其分法必然为第一个分割点为sum[i-1]/3 和第二个分割点为2sum[i-1]/2
因此我们只需要各自二分到区间长度 然后相乘即可
时间复杂度为O(logn) 足足降了一个O(n)
但是比赛时候不好说 只要算复杂度没问题 能做对就行
b.参考代码
class Solution {
public:
const int mod=1e9+7;
int numWays(string s) {
int n=s.size();
vector<int> sum(n,0); //前缀和
sum[0]=s[0]-'0';
for(int i=1;i<n;i++)
if(s[i]-'0')sum[i]=sum[i-1]+1;
else sum[i]=sum[i-1];
int ans=0;
for(int i=0;i<n-2;i++){
//傻傻枚举第一个分割点
int three=sum[n-1],one=sum[i];
if(three-one!=one*2)continue; //不可能的点 其实第一个点也能算出来 比赛怎么想得快怎么来
int l=lower_bound(sum.begin()+i+1,sum.begin()+n-1,one*2)-sum.begin();
int r=upper_bound(sum.begin()+i+1,sum.begin()+n-1,one*2)-sum.begin()-1;
if(!l||!r||l>=n||r>=n)continue;
ans=(ans+r-l+1)%mod; //计数
}
return ans;
}
};
c.删除最短的子数组使剩余数组有序
c.题目
给你一个整数数组 arr ,请你删除一个子数组(可以为空),使得 arr 中剩下的元素是 非递减 的。
一个子数组指的是原数组中连续的一个子序列。
请你返回满足题目要求的最短子数组的长度。
示例 1
输入:arr = [1,2,3,10,4,2,3,5]
输出:3
解释:我们需要删除的最短子数组是 [10,4,2] ,长度为 3 。剩余元素形成非递减数组 [1,2,3,3,5] 。
另一个正确的解为删除子数组 [3,10,4] 。
示例 2
输入:arr = [5,4,3,2,1]
输出:4
解释:由于数组是严格递减的,我们只能保留一个元素。所以我们需要删除长度为 4 的子数组,要么删除 [5,4,3,2],要么删除 [4,3,2,1]。
示例 3
输入:arr = [1,2,3]
输出:0
解释:数组已经是非递减的了,我们不需要删除任何元素。
示例 4
输入:arr = [1]
输出:0
提示
- 1 <= arr.length <= 10^5
- 0 <= arr[i] <= 10^9
c.分析
这道题确实需要一些思考和证明
画画想想猜猜后得出个首要结论:
第一个山峰(即第一个即将开始下降的点)到最后一个谷底(即最后一个即将开始上升的点)之间的肯定是要全部删掉的 因为其之间的都是下坡开始到下坡结束 都是必须要删的
记第一个山峰为pos1 记最后一个谷底为pos2
那么删完中间之后我们会得到 两个非递减区间 (0,pos1)和(pos2,n-1)
对于这两个区间会有以下三种情况:
- arr[pos1]<=arr[pos2] 已经单调递增 不需要操作
- arr[pos1]>arr[pos2] 可以通过枚举一个区间的值 然后再通过二分在另一个区间找到能够平滑连接的值 (两个区间都是单独有序的 所以可以二分
- 左边区间完全大于右边的所以值 这是上面情况的特例 因此我们没办法在另一个区间找到平滑连接的值 因此我们需要枚举究竟是把左边全删还是右边全删比较ok
总的时间复杂度为O(nlogn) 首先是O(n)预处理出山顶和谷底
然后O(n)枚举其中一part的点 O(logn)枚举另外一半
具体看代码
c.参考代码
class Solution {
public:
int findLengthOfShortestSubarray(vector<int>& arr) {
int n=arr.size();
int pos1=-1,pos2=-1;
arr.push_back(INT_MAX);
for(int i=0;i<n;i++){
//找山峰和谷底
if(pos1==-1&&arr[i]>arr[i+1])pos1=i;
else if(pos1!=-1&&arr[i]<arr[i-1])pos2=i;
}
if(pos1==-1)return 0; //没有山峰即表示是升序的
int ans=n-1;
for(int i=pos2;i<n;i++){
//枚举右边的part
int l=0,r=pos1;
while(l<r){
//二分去找能够平滑连接的
int mid=(l+r+1)>>1;
if(arr[mid]<=arr[i])l=mid;
else r=mid-1;
}
if(r>=0&&arr[l]<=arr[i])ans=min(ans,i-l-1); //中间部分全部删掉
}
ans=min(ans,n-pos1-1); //特殊情况 枚举下两边全删
ans=min(ans,pos2);
return ans;
}
};
d.统计所有可行路径
d.题目
给你一个 互不相同 的整数数组,其中 locations[i] 表示第 i 个城市的位置。同时给你 start,finish 和 fuel 分别表示出发城市、目的地城市和你初始拥有的汽油总量
每一步中,如果你在城市 i ,你可以选择任意一个城市 j ,满足 j != i 且 0 <= j < locations.length ,并移动到城市 j 。从城市 i 移动到 j 消耗的汽油量为 |locations[i] - locations[j]|,|x| 表示 x 的绝对值。
请注意, fuel 任何时刻都 不能 为负,且你 可以 经过任意城市超过一次(包括 start 和 finish )。
请你返回从 start 到 finish 所有可能路径的数目。
由于答案可能很大, 请将它对 10^9 + 7 取余后返回。
示例 1
输入:locations = [2,3,6,8,4], start = 1, finish = 3, fuel = 5
输出:4
解释:以下为所有可能路径,每一条都用了 5 单位的汽油:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
示例 2
输入:locations = [4,3,1], start = 1, finish = 0, fuel = 6
输出:5
解释:以下为所有可能的路径:
1 -> 0,使用汽油量为 fuel = 1
1 -> 2 -> 0,使用汽油量为 fuel = 5
1 -> 2 -> 1 -> 0,使用汽油量为 fuel = 5
1 -> 0 -> 1 -> 0,使用汽油量为 fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0,使用汽油量为 fuel = 5
示例 3
输入:locations = [5,2,1], start = 0, finish = 2, fuel = 3
输出:0
解释:没有办法只用 3 单位的汽油从 0 到达 2 。因为最短路径需要 4 单位的汽油。
示**例 4 **
输入:locations = [2,1,5], start = 0, finish = 0, fuel = 3
输出:2
解释:总共有两条可行路径,0 和 0 -> 1 -> 0 。
示例 5
输入:locations = [1,2,3], start = 0, finish = 2, fuel = 40
输出:615088286
解释:路径总数为 2615088300 。将结果对 10^9 + 7 取余,得到 615088286 。
提示
- 2 <= locations.length <= 100
- 1 <= locations[i] <= 10^9
- 所有 locations 中的整数 互不相同 。
- 0 <= start, finish < locations.length
- 1 <= fuel <= 200
d.分析
啊这 这种方案数 很大概率是dp 因此我们可以往这边想
看完题目之后 小分析一波之后可以定下状态表示 dp[i][j]表示 从i出发并且携带j分量的汽油的方案数
那么转移方程也就很简单啦:
对于当前点i 我们我们把除了自身的所有点都去尝试下转移 (只要油够)
那么就是 dp[i][j]=sum(dp[k][j-cost(i,k)]) cost(i,k)<=j
枚举顺序嘛 比赛时候不愿意去想 因此就用了记忆化搜索
枚举的终点是不够油 (而不是走到终点) 走过终点需要+1状态
总的时间复杂度为 总dp数组状态数
d.参考代码
int dp[105][205];
const int mod = 1e9+7;
class Solution {
public:
vector<int> v;
int begin,end;
int countRoutes(vector<int>& locations, int start, int finish, int fuel) {
memset(dp,-1,sizeof(dp));
v=locations;
begin=start;
end=finish;
return ms(start,fuel);
}
int ms(int x,int fuel){
if(dp[x][fuel]!=-1)return dp[x][fuel];
int sum=0;
if(x==end)sum++;
for(int i=0;i<v.size();i++){
if(i==x)continue;
if(abs(v[x]-v[i])<=fuel)sum=(sum+ms(i,fuel-abs(v[x]-v[i])))%mod;
}
return dp[x][fuel]=sum;
}
};