LeetCode 第205场周赛 题解
还行 第一题读错题WA了一发 第二题居然以为1e10是10亿爆int了一发
文章目录
- a.替换所有的问号
-
- a.题目
- a.分析
- a.参考代码
- b.数的平方等于两数乘积的方法数
-
- b.题目
- b.分析
- b.参考代码
- c.避免重复字母的最小删除成本
-
- c.题目
- c.分析
- c.参考代码
- d.保证图可完全遍历
-
- d.题目
- d.分析
- d.参考代码
a.替换所有的问号
a.题目
给你一个仅包含小写英文字母和 ‘?’ 字符的字符串 s ,请你将所有的 ‘?’ 转换为若干小写字母,使最终的字符串不包含任何 连续重复 的字符。
注意:你 不能 修改非 ‘?’ 字符。
题目测试用例保证 除 ‘?’ 字符 之外,不存在连续重复的字符。
在完成所有转换(可能无需转换)后返回最终的字符串。如果有多个解决方案,请返回其中任何一个。可以证明,在给定的约束条件下,答案总是存在的。
示例 1
输入:s = “?zs”
输出:“azs”
解释:该示例共有 25 种解决方案,从 “azs” 到 “yzs” 都是符合题目要求的。只有 “z” 是无效的修改,因为字符串 “zzs” 中有连续重复的两个 ‘z’ 。
示例 2
输入:s = “ubv?w”
输出:“ubvaw”
解释:该示例共有 24 种解决方案,只有替换成 “v” 和 “w” 不符合题目要求。因为 “ubvvw” 和 “ubvww” 都包含连续重复的字符。
示例 3
输入:s = “j?qg??b”
输出:“jaqgacb”
示例 4
输入:s = “??yw?ipkj?”
输出:“acywaipkja”
提示
- 1 <= s.length <= 100
- s 仅包含小写英文字母和 ‘?’ 字符
a.分析
原本还以为是全部不能重复出现 WA了一发
后来才发现原来是隔壁的不能重复
那么就很暴力了:
对于每个问号 都在a~z26个字符中遍历一下 找到和左右都不相同的就可以了
(其实小证明一下后你会发现你只会用到abc)
如果右边也是问号 那么不用管 因为下次到它的时候它会考虑左边的情况
总的时间复杂度为O(Cn) 常数其实为3 不是为26
a.参考代码
class Solution {
public:
string modifyString(string s) {
int n=s.size();
for(int i=0;i<s.size();i++){
if(s[i]=='?'){
char left='%',right='&'; //边界的特殊情况
if(i)left=s[i-1];
if(i<n-1)right=s[i+1];
for(char j='a';j<='c';j++){
//其实到c就行
if(j!=left&&j!=right){
s[i]=j;
break;
}
}
}
}
return s;
}
};
b.数的平方等于两数乘积的方法数
b.题目
给你两个整数数组 nums1 和 nums2 ,请你返回根据以下规则形成的三元组的数目(类型 1 和类型 2 ):
- 类型 1:三元组 (i, j, k) ,如果 nums1[i]2 == nums2[j] * nums2[k] 其中 0 <= i < nums1.length 且 0 <= j < k < nums2.length
- 类型 2:三元组 (i, j, k) ,如果 nums2[i]2 == nums1[j] * nums1[k] 其中 0 <= i < nums2.length 且 0 <= j < k < nums1.length
示例 1
输入:nums1 = [7,4], nums2 = [5,2,8,9]
输出:1
解释:类型 1:(1,1,2), nums1[1]^2 = nums2[1] * nums2[2] (4^2 = 2 * 8
示例 2
输入:nums1 = [1,1], nums2 = [1,1,1]
输出:9
解释:所有三元组都符合题目要求,因为 1^2 = 1 * 1
类型 1:(0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2), nums1[i]^2 = nums2[j] * nums2[k]
类型 2:(0,0,1), (1,0,1), (2,0,1), nums2[i]^2 = nums1[j] * nums1[k]
示例 3
输入:nums1 = [7,7,8,3], nums2 = [1,2,9,7]
输出:2
解释:有两个符合题目要求的三元组
类型 1:(3,0,2), nums1[3]^2 = nums2[0] * nums2[2]
类型 2:(3,0,1), nums2[3]^2 = nums1[0] * nums1[1]
示例 4
输入:nums1 = [4,7,9,11,23], nums2 = [3,5,1024,12,18]
输出:0
解释:不存在符合题目要求的三元组
提示
- 1 <= nums1.length, nums2.length <= 1000
- 1 <= nums1[i], nums2[i] <= 10^5
b.分析
先看数据 1000 那么估计只能是O(n2)或者O(n2logn)能过
考虑排序 (不太可行)
我们发现j和k的先后顺序其实没有关系 只要一对数是不重复的 那么就肯定有先有后
所以我们可以把两个数组都排序 然后遍历等式左边数组进行平方 然后再在另一个数组中 用前后双指针来移动找到目标值 然后问题来了 双指针可以找到一个目标值 但是移动的过程中会漏掉一些组合 所以行不通
再考虑暴力预处理 (过了)
分析等式 等式的左边我们是可以通过遍历每个数然后平方得出来的
那么有没有可能等式右边的我们也能直接得出来呢?
细想一下发现是可以的 因为右边一共的组合就O(n^2)种 可以暴力预处理
然后以乘积为key 乘积的个数为value 存在一个hash map中
那么在遍历等式左边的每一个 就可以直接获取有多少个乘积相等的右边式子了
总的复杂度为预处理时候的O(n^2) 后面遍历的时候 只需要O(n)遍历
b.参考代码
class Solution {
public:
int numTriplets(vector<int>& nums1, vector<int>& nums2) {
unordered_map<long long,int> mp1,mp2;
for(int i=0;i<nums1.size()-1;i++)
for(int j=i+1;j<nums1.size();j++)
mp1[1ll*nums1[i]*nums1[j]]++;
for(int i=0;i<nums2.size()-1;i++)
for(int j=i+1;j<nums2.size();j++)
mp2[1ll*nums2[i]*nums2[j]]++;
int ans=0;
for(int i=0;i<nums1.size();i++)
ans+=mp2[1ll*nums1[i]*nums1[i]];
for(int j=0;j<nums2.size();j++)
ans+=mp1[1ll*nums2[j]*nums2[j]];
return ans;
}
};
c.避免重复字母的最小删除成本
c.题目
给你一个字符串 s 和一个整数数组 cost ,其中 cost[i] 是从 s 中删除字符 i 的代价。
返回使字符串任意相邻两个字母不相同的最小删除成本。
请注意,删除一个字符后,删除其他字符的成本不会改变。
示例 1
输入:s = “abaac”, cost = [1,2,3,4,5]
输出:3
解释:删除字母 “a” 的成本为 3,然后得到 “abac”(字符串中相邻两个字母不相同)。
示例 2
输入:s = “abc”, cost = [1,2,3]
输出:0
解释:无需删除任何字母,因为字符串中不存在相邻两个字母相同的情况。
示例 3
输入:s = “aabaa”, cost = [1,2,3,4,1]
输出:2
解释:删除第一个和最后一个字母,得到字符串 (“aba”) 。
提示
- s.length == cost.length
- 1 <= s.length, cost.length <= 10^5
- 1 <= cost[i] <= 10^4
- s 中只含有小写英文字母
c.分析
本来还以为要用dp的 后来编几个样例跑了一下 发现是可以贪心的
从左向右遍历 如果当前和前一个不同 自然不用管
如果当前和前面相同 这么前面的和当前的肯定是要删除一个的了
(此时前面的相同只会剩下一个 因为之前的也肯定会像当前操作这样干)
但是问题来了 删除前面的 并不指的是删除前面一个
其实这里只需要把剩下的那一个的cost值移到最后就行了 那么后面比较的时候就等价于和前面剩下那个比较了
c.参考代码
class Solution {
public:
int minCost(string s, vector<int>& cost) {
int ans=0;
for(int i=1;i<s.size();i++){
if(s[i]!=s[i-1])continue; //不重复就没所谓了
if(cost[i-1]<=cost[i])ans+=cost[i-1];
else{
ans+=cost[i];
swap(cost[i-1],cost[i]); //把剩下的移动到最后 才能给后续的比较
}
}
return ans;
}
};
d.保证图可完全遍历
d.题目
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
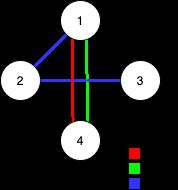
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1**,1**,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
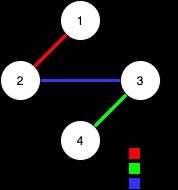
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示
- 1 <= n <= 10^5
- 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
- edges[i].length == 3
- 1 <= edges[i][0] <= 3
- 1 <= edges[i][1] < edges[i][2] <= n
- 所有元组 (typei, ui, vi) 互不相同
d.分析
有一点可以肯定的是 删完之后肯定是一棵树 即边数为n-1
再分析可以肯定第二点是 根据最小生成树的原理 只要不成环 就证明这条边时关建边 也就是我们需要删除掉所有的非关键边
根据Kruskal算法思想 采用并查集可以得到要删除的边
即当前边ab 在并查集中已经是连通了的 表示ab加上后会成环 因此要删除
这道题有个细节就是 需要先枚举公共边删掉公共边的非关键边
然后再分别处理两个人的非关键边
具体原因就是因为先处理公共边 可以处理类似于三边平行的情况
最后就是要看一下删完非关键边后的边数是否等于n-1 如果不是 那么就证明原图是不连通的
总得时间复杂度为遍历所有边的O(n) 假设并查集是路径压缩的O(1)
(其实并查集即使路径压缩了还是没那么快)
d.参考代码
const int N=1e5+5;
int f1[N],f2[N];
void init(int n){
//并查集初始化
for(int i=0;i<=n;i++){
f1[i]=i;
f2[i]=i;
}
}
int find1(int x){
//并查集找祖先
return f1[x]=(f1[x]==x)?x:find1(f1[x]);
}
int find2(int x){
return f2[x]=(f2[x]==x)?x:find2(f2[x]);
}
inline void union1(int a,int b){
//合并
f1[find1(a)]=find1(b);
}
inline void union2(int a,int b){
f2[find2(a)]=find2(b);
}
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
init(n);
vector<pair<int,int>> e1,e2,e3; //三种边
for(int i=0;i<edges.size();i++){
int type=edges[i][0],a=edges[i][1],b=edges[i][2];
if(type==1)e1.push_back({
a,b});
else if(type==2)e2.push_back({
a,b});
else if(type==3)e3.push_back({
a,b});
else return -1;
}
int ans=0,cnt1=0,cnt2=0; //删掉的边数和两个图的总边数
for(int i=0;i<e3.size();i++){
//先处理公共边
int a=e3[i].first,b=e3[i].second;
if(find1(a)==find1(b))ans++;
else {
union1(a,b);
cnt1++;
union2(a,b);
cnt2++;
}
}
for(int i=0;i<e1.size();i++){
int a=e1[i].first,b=e1[i].second;
if(find1(a)==find1(b))ans++;
else {
union1(a,b);
cnt1++;
}
}
for(int i=0;i<e2.size();i++){
int a=e2[i].first,b=e2[i].second;
if(find2(a)==find2(b))ans++;
else {
union2(a,b);
cnt2++;
}
}
if(cnt1!=n-1||cnt2!=n-1)return -1; //非连通图
return ans;
}
};