OpenSSL源码分析之MD5算法
MD5算法的基本流程如下(流程参考自http://kmplayer.iteye.com/blog/628936):
-
对每个流程作出解释:
信息填充
目的:使信息位长度恰好是512的整数倍。
填充的方法:在信息的后面填充一个1和无数个0,直到使信息的位长(BitsLength)将被扩展至N*512+448,才停止用0对信息的填充。然后,在这个结果后面附加一个以64位二进制表示的填充前信息长度。这样做的原因是为满足后面处理中对信息长度的要求。
主循环操作
首先给定链接变量,具体包括四个32位的整数参数,分别为:A=0x01234567,B=0x89abcdef,C=0xfedcba98,D=0x76543210
将上面四个链接变量复制到另外四个变量中:A到a,B到b,C到c,D到d。
将当前将要处理的512位信息分成16组,每组32位,分别表示为:M0,M1,……,M15。
ti表示一个常数,可以如下选择:在第i步中,ti是4294967296*abs(sin(i))的整数部分,i的单位是弧度。
每轮循环操作都很相似,都要进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算,然后将所得结果加上第四个变量,文本的一个子分组Mj和一个常数ti。再将所得结果向右环移一个不定的数s,并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。每次轮循环可以表示成
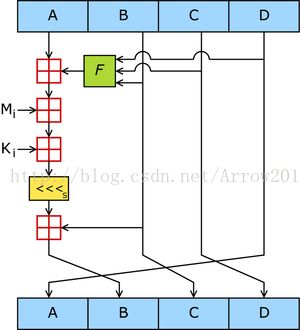
一轮循环
第一轮循环所用到的非线性函数:F(X,Y,Z)=(X&Y)|((~X)&Z)。
每一次操作可以表示为FF(a,b, c, d, Mj, s, ti):a= b + ((a + F(b, c, d) + Mj + ti) <
第一轮的16次操作可以分别表示为:
FF(a,b, c, d, M0, 7, 0xd76aa478)
FF(d, a, b, c, M1, 12,0xe8c7b756)
FF(c, d, a, b, M2, 17, 0x242070db)
FF(b, c, d, a,M3, 22, 0xc1bdceee)
FF(a, b, c, d, M4, 7, 0xf57c0faf)
FF(d, a,b, c, M5, 12, 0x4787c62a)
FF(c, d, a, b, M6, 17,0xa8304613)
FF(b, c, d, a, M7, 22, 0xfd469501)
FF(a, b, c, d,M8, 7, 0x698098d8)
FF(d, a, b, c, M9, 12, 0x8b44f7af)
FF(c, d,a, b, M10, 17, 0xffff5bb1)
FF(b, c, d, a, M11, 22,0x895cd7be)
FF(a, b, c, d, M12, 7, 0x6b901122)
FF(d, a, b, c,M13, 12, 0xfd987193)
FF(c, d, a, b, M14, 17, 0xa679438e)
FF(b,c, d, a, M15, 22, 0x49b40821)
二轮循环
第二轮循环所用到的非线性函数:G(X,Y,Z)=(X&Z)|(Y&(~Z))。
每一次操作可以表示为GG(a,b, c, d, Mj, s, ti):a= b + ((a + G(b, c, d) + Mj + ti) <
第二轮的16次操作可以分别表示为:
GG(a,b, c, d, M1, 5, 0xf61e2562)
GG(d, a, b, c, M6, 9,0xc040b340)
GG(c, d, a, b, M11, 14, 0x265e5a51)
GG(b, c, d, a,M0, 20, 0xe9b6c7aa)
GG(a, b, c, d, M5, 5, 0xd62f105d)
GG(d, a,b, c, M10, 9, 0x02441453)
GG(c, d, a, b, M15, 14,0xd8a1e681)
GG(b, c, d, a, M4, 20, 0xe7d3fbc8)
GG(a, b, c, d,M9, 5, 0x21e1cde6)
GG(d, a, b, c, M14, 9, 0xc33707d6)
GG(c, d,a, b, M3, 14, 0xf4d50d87)
GG(b, c, d, a, M8, 20,0x455a14ed)
GG(a, b, c, d, M13, 5, 0xa9e3e905)
GG(d, a, b, c,M2, 9, 0xfcefa3f8)
GG(c, d, a, b, M7, 14, 0x676f02d9)
GG(b, c,d, a, M12, 20, 0x8d2a4c8a)
三轮循环
第三轮循环所用到的非线性函数:H(X,Y,Z)=X^Y^Z。
每一次操作可以表示为HH(a,b, c, d, Mj, s, ti):a= b + ((a + H(b, c, d) + Mj + ti) <
第三轮的16次操作可以分别表示为:
HH(a,b, c, d, M5, 4, 0xfffa3942)
HH(d, a, b, c, M8, 11,0x8771f681)
HH(c, d, a, b, M11, 16, 0x6d9d6122)
HH(b, c, d, a,M14, 23, 0xfde5380c)
HH(a, b, c, d, M1, 4, 0xa4beea44)
HH(d,a, b, c, M4, 11, 0x4bdecfa9)
HH(c, d, a, b, M7, 16,0xf6bb4b60)
HH(b, c, d, a, M10, 23, 0xbebfbc70)
HH(a, b, c, d,M13, 4, 0x289b7ec6)
HH(d, a, b, c, M0, 11, 0xeaa127fa)
HH(c,d, a, b, M3, 16, 0xd4ef3085)
HH(b, c, d, a, M6, 23,0x04881d05)
HH(a, b, c, d, M9, 4, 0xd9d4d039)
HH(d, a, b, c,M12, 11, 0xe6db99e5)
HH(c, d, a, b, M15, 16, 0x1fa27cf8)
HH(b,c, d, a, M2, 23, 0xc4ac5665)
四轮循环
第四轮循环所用到的非线性函数:I(X,Y,Z)=Y^(X|(~Z))。
每一次操作可以表示为:II(a,b, c, d, Mj, s, ti)表示a= b + ((a + I(b, c, d) + Mj + ti) <
第四轮的16次操作可以分别表示为:
II(a,b, c, d, M0, 6, 0xf4292244)
II(d, a, b, c, M7, 10,0x432aff97)
II(c, d, a, b, M14, 15, 0xab9423a7)
II(b, c, d, a,M5, 21, 0xfc93a039)
II(a, b, c, d, M12, 6, 0x655b59c3)
II(d,a, b, c, M3, 10, 0x8f0ccc92)
II(c, d, a, b, M10, 15,0xffeff47d)
II(b, c, d, a, M1, 21, 0x85845dd1)
II(a, b, c, d,M8, 6, 0x6fa87e4f)
II(d, a, b, c, M15, 10, 0xfe2ce6e0)
II(c,d, a, b, M6, 15, 0xa3014314)
II(b, c, d, a, M13, 21,0x4e0811a1)
II(a, b, c, d, M4, 6, 0xf7537e82)
II(d, a, b, c,M11, 10, 0xbd3af235)
II(c, d, a, b, M2, 15, 0x2ad7d2bb)
II(b,c, d, a, M9, 21,0xeb86d391)
所有这些完成之后,将A、B、C、D分别加上a、b、c、d。然后用下一分组数据继续运行算法,最后的输出是A、B、C和D的级联。
2.在OpenSSL中的源码
在OpenSSL中,MD5算法的源码在crypto/md5文件中,和OpenSSL中的其他哈希函数一样,MD5的实现也是主要由初始化函数fips_md_init、加密函数HASH_UPDATE、和结果处理函数HASH_FINAL,其中HASH_UPDATE需要使用块加密函数HASH_BLOCK_DATA_ORDER。这些函数的宏定义分别分布在crypto.h(fips_md_init)和md32_common.h(HASH_UPDATE、HASH_FINAL、HASH_BLOCK_DATA_ORDER)中并在md5.h的头文件中转换成相应的函数名,主要思路还是和上次解析的md4函数一样,就不做叙述了。贴上笔者抠出来的可以在X86上独立编译的md5算法模块。
#include
#include
#define MD5_LONG unsigned long
#define MD5_CBLOCK 64
#define MD5_LBLOCK (MD5_CBLOCK/4)
#define MD5_DIGEST_LENGTH 16
#define MD32_REG_T long
#define DATA_ORDER_IS_LITTLE_ENDIAN
#define INIT_DATA_A (unsigned long)0x67452301L
#define INIT_DATA_B (unsigned long)0xefcdab89L
#define INIT_DATA_C (unsigned long)0x98badcfeL
#define INIT_DATA_D (unsigned long)0x10325476L
#define ROTATE(a,n) (((a)<<(n))|(((a)&0xffffffff)>>(32-(n))))
#define HOST_c2l(c,l) (l =(((unsigned long)(*((c)++))) ), \
l|=(((unsigned long)(*((c)++)))<< 8), \
l|=(((unsigned long)(*((c)++)))<<16), \
l|=(((unsigned long)(*((c)++)))<<24) )
#define HOST_l2c(l,c) (*((c)++)=(unsigned char)(((l) )&0xff), \
*((c)++)=(unsigned char)(((l)>> 8)&0xff), \
*((c)++)=(unsigned char)(((l)>>16)&0xff), \
*((c)++)=(unsigned char)(((l)>>24)&0xff), \
l)
#define HASH_MAKE_STRING(c,s) do { \
unsigned long ll; \
ll=(c)->A; (void)HOST_l2c(ll,(s)); \
ll=(c)->B; (void)HOST_l2c(ll,(s)); \
ll=(c)->C; (void)HOST_l2c(ll,(s)); \
ll=(c)->D; (void)HOST_l2c(ll,(s)); \
} while (0)
#define F(b,c,d) ((((c) ^ (d)) & (b)) ^ (d))
#define G(b,c,d) ((((b) ^ (c)) & (d)) ^ (c))
#define H(b,c,d) ((b) ^ (c) ^ (d))
#define I(b,c,d) (((~(d)) | (b)) ^ (c))
#define R0(a,b,c,d,k,s,t) { \
a+=((k)+(t)+F((b),(c),(d))); \
a=ROTATE(a,s); \
a+=b; };\
#define R1(a,b,c,d,k,s,t) { \
a+=((k)+(t)+G((b),(c),(d))); \
a=ROTATE(a,s); \
a+=b; };
#define R2(a,b,c,d,k,s,t) { \
a+=((k)+(t)+H((b),(c),(d))); \
a=ROTATE(a,s); \
a+=b; };
#define R3(a,b,c,d,k,s,t) { \
a+=((k)+(t)+I((b),(c),(d))); \
a=ROTATE(a,s); \
a+=b; };
typedef struct MD5state_st1{
MD5_LONG A,B,C,D;
MD5_LONG Nl,Nh;
MD5_LONG data[MD5_LBLOCK];
unsigned int num;
}MD5_CTX;
unsigned char cleanse_ctr = 0;
int MD5_Init(MD5_CTX *c){
memset (c,0,sizeof(*c));
c->A=INIT_DATA_A;
c->B=INIT_DATA_B;
c->C=INIT_DATA_C;
c->D=INIT_DATA_D;
return 1;
}
void md5_block_data_order(MD5_CTX *c, const void *data_, size_t num){
const unsigned char *data=data_;
register unsigned MD32_REG_T A,B,C,D,l;
#ifndef MD32_XARRAY
/* See comment in crypto/sha/sha_locl.h for details. */
unsigned MD32_REG_T XX0, XX1, XX2, XX3, XX4, XX5, XX6, XX7,
XX8, XX9,XX10,XX11,XX12,XX13,XX14,XX15;
# define X(i) XX##i
#else
MD5_LONG XX[MD5_LBLOCK];
# define X(i) XX[i]
#endif
A=c->A;
B=c->B;
C=c->C;
D=c->D;
for (;num--;){
HOST_c2l(data,l); X( 0)=l; HOST_c2l(data,l); X( 1)=l;
/* Round 0 */
R0(A,B,C,D,X( 0), 7,0xd76aa478L); HOST_c2l(data,l); X( 2)=l;
R0(D,A,B,C,X( 1),12,0xe8c7b756L); HOST_c2l(data,l); X( 3)=l;
R0(C,D,A,B,X( 2),17,0x242070dbL); HOST_c2l(data,l); X( 4)=l;
R0(B,C,D,A,X( 3),22,0xc1bdceeeL); HOST_c2l(data,l); X( 5)=l;
R0(A,B,C,D,X( 4), 7,0xf57c0fafL); HOST_c2l(data,l); X( 6)=l;
R0(D,A,B,C,X( 5),12,0x4787c62aL); HOST_c2l(data,l); X( 7)=l;
R0(C,D,A,B,X( 6),17,0xa8304613L); HOST_c2l(data,l); X( 8)=l;
R0(B,C,D,A,X( 7),22,0xfd469501L); HOST_c2l(data,l); X( 9)=l;
R0(A,B,C,D,X( 8), 7,0x698098d8L); HOST_c2l(data,l); X(10)=l;
R0(D,A,B,C,X( 9),12,0x8b44f7afL); HOST_c2l(data,l); X(11)=l;
R0(C,D,A,B,X(10),17,0xffff5bb1L); HOST_c2l(data,l); X(12)=l;
R0(B,C,D,A,X(11),22,0x895cd7beL); HOST_c2l(data,l); X(13)=l;
R0(A,B,C,D,X(12), 7,0x6b901122L); HOST_c2l(data,l); X(14)=l;
R0(D,A,B,C,X(13),12,0xfd987193L); HOST_c2l(data,l); X(15)=l;
R0(C,D,A,B,X(14),17,0xa679438eL);
R0(B,C,D,A,X(15),22,0x49b40821L);
/* Round 1 */
R1(A,B,C,D,X( 1), 5,0xf61e2562L);
R1(D,A,B,C,X( 6), 9,0xc040b340L);
R1(C,D,A,B,X(11),14,0x265e5a51L);
R1(B,C,D,A,X( 0),20,0xe9b6c7aaL);
R1(A,B,C,D,X( 5), 5,0xd62f105dL);
R1(D,A,B,C,X(10), 9,0x02441453L);
R1(C,D,A,B,X(15),14,0xd8a1e681L);
R1(B,C,D,A,X( 4),20,0xe7d3fbc8L);
R1(A,B,C,D,X( 9), 5,0x21e1cde6L);
R1(D,A,B,C,X(14), 9,0xc33707d6L);
R1(C,D,A,B,X( 3),14,0xf4d50d87L);
R1(B,C,D,A,X( 8),20,0x455a14edL);
R1(A,B,C,D,X(13), 5,0xa9e3e905L);
R1(D,A,B,C,X( 2), 9,0xfcefa3f8L);
R1(C,D,A,B,X( 7),14,0x676f02d9L);
R1(B,C,D,A,X(12),20,0x8d2a4c8aL);
/* Round 2 */
R2(A,B,C,D,X( 5), 4,0xfffa3942L);
R2(D,A,B,C,X( 8),11,0x8771f681L);
R2(C,D,A,B,X(11),16,0x6d9d6122L);
R2(B,C,D,A,X(14),23,0xfde5380cL);
R2(A,B,C,D,X( 1), 4,0xa4beea44L);
R2(D,A,B,C,X( 4),11,0x4bdecfa9L);
R2(C,D,A,B,X( 7),16,0xf6bb4b60L);
R2(B,C,D,A,X(10),23,0xbebfbc70L);
R2(A,B,C,D,X(13), 4,0x289b7ec6L);
R2(D,A,B,C,X( 0),11,0xeaa127faL);
R2(C,D,A,B,X( 3),16,0xd4ef3085L);
R2(B,C,D,A,X( 6),23,0x04881d05L);
R2(A,B,C,D,X( 9), 4,0xd9d4d039L);
R2(D,A,B,C,X(12),11,0xe6db99e5L);
R2(C,D,A,B,X(15),16,0x1fa27cf8L);
R2(B,C,D,A,X( 2),23,0xc4ac5665L);
/* Round 3 */
R3(A,B,C,D,X( 0), 6,0xf4292244L);
R3(D,A,B,C,X( 7),10,0x432aff97L);
R3(C,D,A,B,X(14),15,0xab9423a7L);
R3(B,C,D,A,X( 5),21,0xfc93a039L);
R3(A,B,C,D,X(12), 6,0x655b59c3L);
R3(D,A,B,C,X( 3),10,0x8f0ccc92L);
R3(C,D,A,B,X(10),15,0xffeff47dL);
R3(B,C,D,A,X( 1),21,0x85845dd1L);
R3(A,B,C,D,X( 8), 6,0x6fa87e4fL);
R3(D,A,B,C,X(15),10,0xfe2ce6e0L);
R3(C,D,A,B,X( 6),15,0xa3014314L);
R3(B,C,D,A,X(13),21,0x4e0811a1L);
R3(A,B,C,D,X( 4), 6,0xf7537e82L);
R3(D,A,B,C,X(11),10,0xbd3af235L);
R3(C,D,A,B,X( 2),15,0x2ad7d2bbL);
R3(B,C,D,A,X( 9),21,0xeb86d391L);
A = c->A += A;
B = c->B += B;
C = c->C += C;
D = c->D += D;
}
}
int MD5_Update(MD5_CTX *c, const void *data_, size_t len){
const unsigned char *data=data_;
unsigned char *p;
MD5_LONG l;
size_t n;
if (len==0) return 1;
l=(c->Nl+(((MD5_LONG)len)<<3))&0xffffffffUL;
if (l < c->Nl)
c->Nh++;
c->Nh+=(MD5_LONG)(len>>29);
c->Nl=l;
n = c->num;
if (n != 0){
p=(unsigned char *)c->data;
if (len >= MD5_CBLOCK || len+n >= MD5_CBLOCK){
memcpy (p+n,data,MD5_CBLOCK-n);
md5_block_data_order(c,p,1);
n = MD5_CBLOCK-n;
data += n;
len -= n;
c->num = 0;
memset (p,0,MD5_CBLOCK);
}else{
memcpy (p+n,data,len);
c->num += (unsigned int)len;
return 1;
}
}
n = len/MD5_CBLOCK;
if (n > 0){
md5_block_data_order(c,data,n);
n *= MD5_CBLOCK;
data += n;
len -= n;
}
if (len != 0){
p = (unsigned char *)c->data;
c->num = (unsigned int)len;
memcpy (p,data,len);
}
return 1;
}
int MD5_Final(unsigned char *md, MD5_CTX *c){
unsigned char *p = (unsigned char *)c->data;
size_t n = c->num;
p[n] = 0x80; /* there is always room for one */
n++;
if (n > (MD5_CBLOCK-8)){
memset (p+n,0,MD5_CBLOCK-n);
n=0;
md5_block_data_order(c,p,1);
}
memset (p+n,0,MD5_CBLOCK-8-n);
p += MD5_CBLOCK-8;
#if defined(DATA_ORDER_IS_BIG_ENDIAN)
(void)HOST_l2c(c->Nh,p);
(void)HOST_l2c(c->Nl,p);
#elif defined(DATA_ORDER_IS_LITTLE_ENDIAN)
(void)HOST_l2c(c->Nl,p);
(void)HOST_l2c(c->Nh,p);
#endif
p -= MD5_CBLOCK;
md5_block_data_order(c,p,1);
c->num=0;
memset (p,0,MD5_CBLOCK);
#ifndef HASH_MAKE_STRING
#error "HASH_MAKE_STRING must be defined!"
#else
HASH_MAKE_STRING(c,md);
#endif
return 1;
}
void OPENSSL_cleanse(void *ptr, size_t len){
unsigned char *p = ptr;
size_t loop = len, ctr = cleanse_ctr;
while(loop--){
*(p++) = (unsigned char)ctr;
ctr += (17 + ((size_t)p & 0xF));
}
p=memchr(ptr, (unsigned char)ctr, len);
if(p)
ctr += (63 + (size_t)p);
cleanse_ctr = (unsigned char)ctr;
}
unsigned char *MD5(const unsigned char *d, size_t n, unsigned char *md){
MD5_CTX c;
static unsigned char m[MD5_DIGEST_LENGTH];
if (md == NULL) md=m;
if (!MD5_Init(&c))
return NULL;
MD5_Update(&c,d,n);
MD5_Final(md,&c);
OPENSSL_cleanse(&c,sizeof(c));
return(md);
}
int main(){
unsigned char in[]="12345678987";
/*out = 55 ff 40 9e 85 05 61 0c 02 8a d5 d4 ff a5 ea f7*/
unsigned char out[20];
size_t n;
int i;
n = strlen((const char*)in);
MD5(in,n,out);
printf("\n\nMD5 digest result :\n");
for(i=0;i<16;i++)
printf("%02x ",out[i]);
printf("\n");
} 