平面最近点对 洛谷1257 分治 c++

题目描述

---

给定平面上n个点，找出其中的一对点的距离，使得在这n个点的所有点对中，该距离为所有点对中最小的。

输入格式：

---

第一行：n；2≤n≤10000

接下来n行：每行两个实数：x y，表示一个点的行坐标和列坐标，中间用一个空格隔开。

输出格式：

---

仅一行，一个实数，表示最短距离，精确到小数点后面4位。

说明

---

本题爆搜即可

Solution

---

嗯，这么良心的说明已经少见了

一直想刷的分治题。首先将点图排序、分成左右两半，分别得出左右两半的最近距离

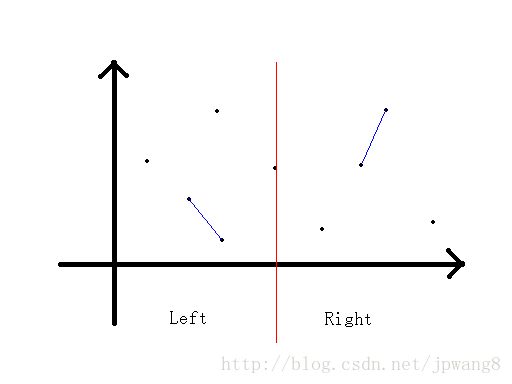
然后可以看出蓝色的线段分别是两部分的最短距离(意思一下)

若递归得来的最短距离为d，那么可知合并答案时新的最近点对可能出现在这个区间
我才没有偷偷加点呢哼

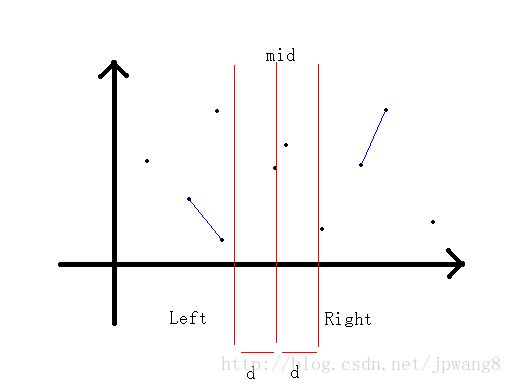
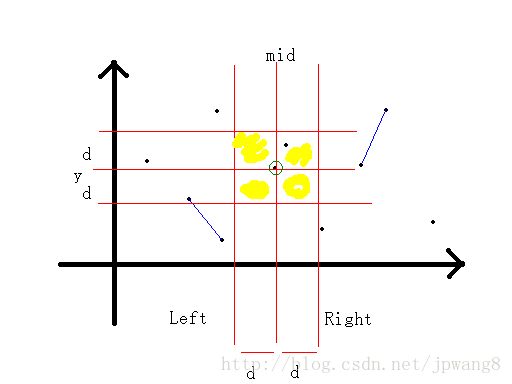
也就是 mid−d 一直到 mid+d 这一段，为什么呢？
显然不证

那么我们可以筛选一批点出来，在这里面找跨越分界线的最近点对
再竖着看，显然对于一个纵坐标为y的点只有 y−mid 到 y+mid 这一段可能有最近点

为什么呢？
显然不证(滑稽

然后根据鸽巢原理，这样符合条件的点是最多只有6个的
然后就A了嗯
还有那道数据加强版过不了是为什么

Code

---

#include 
#include 
#include 
#include 
#define rep(i, a, b) for (int i = a; i <= b; i += 1)
#define fill(x, t) memset(x, t, sizeof(x))
#define INF 0x3f3f3f3f
#define N 10001
using namespace std;
struct pos{
    int x, y;
}p[N];
inline int read(){
    int x = 0, v = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9'){
        if (ch == '-'){
            v = -1;
        }
        ch = getchar();
    }
    while (ch <= '9' && ch >= '0'){
        x = (x << 1) + (x << 3) + ch - '0';
        ch = getchar();
    }
    return x * v;
}
inline double dist(const pos &a, const pos &b){
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
inline double min(const double &x, const double &y){
    return xinline int cmp2(const pos &a, const pos &b){
    return a.y < b.y;
}
inline double getAns(const int &l, const int &r){
    int mid = (l + r) >> 1;
    if (l == r){
        return INF;
    }
    if (l + 1 == r){
        return dist(p[l], p[r]);
    }
    double d = min(getAns(l, mid), getAns(mid + 1, r));
    vector v;
    rep(i, l, r){
        if (fabs(p[i].x - p[mid].x) <= d){
            v.push_back(p[i]);
        }
    }
    sort(v.begin(), v.end(), cmp2);
    rep(i, 0, v.size() - 1){
        rep(j, i + 1, v.size() - 1){
            if (v[j].y - v[i].y < d){
                d = min(d, dist(v[i], v[j]));
            }
        }
    }
    return d;
}
inline int cmp1(const pos &a, const pos &b){
    return a.x < b.x || a.x == b.x && a.y < b.y;
}
int main(void){
    int n = read();
    rep(i, 1, n){
        int x = read(), y = read();
        p[i] = (pos){x, y};
    }
    sort(p + 1, p + n + 1, cmp1);
    double ans = getAns(1, n);
    printf("%.4f\n", ans);
    return 0;
}