第二篇--MATLAB图形可视化(一)

1.二维平面图形与坐标系

1.1 线性坐标曲线plot

• 它是一个线性绘图函数，可以生成线段，曲线和参数方程曲线的函数图像。
• 命令格式：plot(x,y)或者plot(x1,y1,x2,y1,…)
• 示例：绘制正弦余弦函数。

 x=0:0.01:2*pi;
 y=[sin(x);cos(x)]; 
 plot(x,y)  

1.2二维函数曲线fplot

• 专门用于绘制函数y=f(x)图像，数据点是自适应产生的，可以用fplot函数绘出导数变化大的函数图像。
• 命令格式：[X,Y]=fplot(‘fun’,lims)
• fun:函数名字符串；
• lims:定义x的取值区间，lims=[xmin,xmax].
• 线型与颜色
  常用的的线段，颜色与标记参数

颜色		线型		顶点标记
符号	含义	符号	含义	符号	含义	符号	含义
b	蓝色	-	实线	.	实点标记	$\Lambda$	朝上三角符
g	绿色	：	虚线	o	圆圈标记	<	朝左三角符
r	红色	-.	点划线	X	叉字符标记	>	朝右三角符
c	青色	- -	双划线	+	加号标记	p	五角星符
m	洋红			*	星号标记	h	六角形符
y	黄色			s	方块标记
k	黑色			d	菱形标记
w	白色			v	朝下三角符

• 调用格式：plot(x,y,s)，s为类型说明参数，s字符串可选如上三种类型符号之一或者组合形式。
• 实例

t1=0:0.1:2*pi;
t2=0:0.1:6; 
y1=sin(t1);  
y2=sqrt(t2);       
plot(t1,y1,':hb',t2,y2,'--g') 

1.3图像窗口分割subplot

• 实现在同一个窗口中同时显示多个图像的命令
• 命令格式：subplot(m,n,i),将图形窗口分割为m行n列子窗口，i为当前窗口。
• 示例;窗口分割

subplot(2,2,1)  
t=0.1:0.1:2*pi;  
y=sin(t);  
semilogx(t,y)  
grid on   
subplot(2,2,2)  
t=0:0.1:4*pi;  
y=sin(t);  
plot(t,y) 
subplot(2,2,3)  
x=1:0.01:5;  
y=exp(x);  
plotyy(x,y,x,y,’semilogx’,’plot’)   
subplot(2,2,4)  
x=1:0.1:10;  
y=sqrt(x);  
plot(x,y,’:rd’) 

1.4坐标系调整

• 实现坐标系的调整的命令是 axis 函数
• 命令格式： axis([xmin,xmax,ymin,ymax,zmin,zmax])
• 示例：坐标系调整，

subplot(2,1,1)  
t=0:0.1:4*pi;  
y=sin(t);  
plot(t,y)   
subplot(2,1,2)  
t=0:0.1:4*pi;  
y=sin(t);  
plot(t,y)  
axis([0,max(t),min(y),max(y)])  

2.三维绘图命令

2.1三维曲线绘图plot3

• 用来表现单参数的三维曲线。
• 命令格式：plot3(X1,Y1,Z1,s1,X2,Y2,Z2,s2,…)
• Xn、Yn、Zn：第一到三维数据，是尺寸相等的向量/矩阵；
• s、s1、s2：是字符串，用来设置线型、颜色、数据点标记。
• 示例：x,y,z为矩阵。

[X,Y]=meshgrid(-pi:0.1:pi);%生成网格点矩阵 
Z=sin(X)+cos(Y);  
plot3(X,Y,Z)  

2.2三维曲面绘图命令

2.2.1 平面网格点生成

• 函数命令meshgrid 用来生成 x-y 平面上的网格点矩阵， 将由两个向量决定的区域转换为对应的网格点矩阵
• 命令格式：[X,Y]=meshgrid(x,y) 或者 [X,Y]=meshgrid(x) 等价于[X,Y]=meshgrid(x,x)
• 参数含义如下：
• x：是区间[x0,xm]上分划的向量；
• y：是区间[y0,yn]上分划的向量；
• X，Y：输出变量矩阵，矩阵 X 的行向量都是向量 x，矩阵 Y 的列向 量都是向量 y。
• 示例：

[X,Y] = meshgrid(-2:2:2, -2:2:2);  
[X,Y]       %将划分结果输出至矩阵  
ans =          
-2          0          2        -2        -2        -2  
-2          0          2         0          0          0          -2          0          2         2          2          2

2.2.2 三维网格命令mesh

• 命令格式：
• mesh(X，Y，Z，C)：X、Y、Z、C 是同维数的矩阵，X、Y、Z 对 应空间上的网格点，网格线颜色由C决定；
• mesh(X，Y，Z)：相当于上面的 C=Z 的情况；
• mesh(x，y，Z，C)：x 和 y 是向量，Z 和 C 是同维数的矩阵，网格 曲面的网格顶点是（ x(j)，y(i)，Z(i,j)），网格线的颜色由矩阵 C 决 定；
• mesh(x，y，Z)：相当于上面的 C=Z 的情况；
• mesh(Z，C)：等价于 mesh(x，y，Z，C)，此时向量x=1:n，向量 y=1:m；
• mesh(Z)：相当于上面的 C=Z 的情况
• mesh(…,’PropertyName’,PropertyValue,…)：给函mesh设置曲面属性。
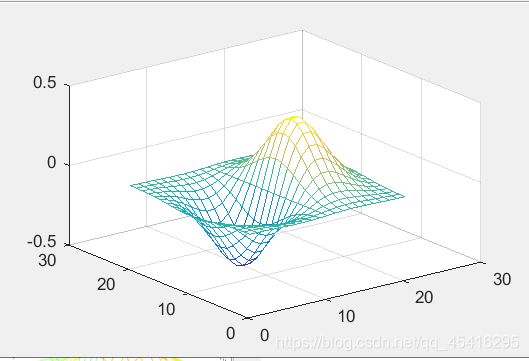
• 示例：

 [X,Y] = meshgrid(-2:2:2, -2:2:2);
 Z = X .* exp(-X.^2 - Y .^2);    
 mesh(Z) 

2.2.3 三维表面命令surf

• 函数 surf 可实现对网格曲面片进行着色，将网格曲面转化 为实曲面。
• 命令格式：surf(z)
• 示例;

z=peaks;      %绘制山峰的图像，将函数值赋予变量z  
surf(z)          %对山峰的图像进行着色处理 
shading interp  %函数 shading 改变着色方式 

3.总结

MATLAB二维及三维绘图的学习分享就到这儿，下一篇即将说到等高线图形绘制及控制图形可视化的效果，敬请期待，如有错误，不吝赐教。