PCA算法人脸识别小结--原理到实现
近段时间学习提取图像特征的算法,研究了一下PCA(主成分分析)算法,用PCA实现了人脸识别,做个小结。
以下是关于PCA算法原理理解较有帮助的资料(关于PCA的资料很多,我觉得看以下的足够了):
1、A tutorial on Principal Components Analysis,Lindsay I Smith,February 26, 2002
2、A Tutorial on Principal Component Analysis,Jonathon Shlens,December 10, 2005; Version 2
3、A Singularly Valuable Decomposition: The SVD of a Matrix,Dan Kalman,February 13, 2002 (求解协方差矩阵的特征向量时我用SVD算法,这是SVD理论的资料)
4、基于PCA 和FLD 的人脸识别方法,张良,December 2012.(里面PCA步骤那部分,构造协方差矩阵和测试部分和原理有出入,值得推敲)
5、松子茶博文,很赞,看完就知道PCA每个步骤的目的和意义,思路就很清晰:
http://blog.csdn.net/songzitea/article/details/18219237
6、斯坦福大学机器学习课程公开课,主成分分析和奇异值分解那两个讲座。
PCA(主成分分析)算法,就是把数据进行压缩。找到一个低维空间,将一组高维数据映射到这个低维空间中,用更少数据量表示重要的信息。
PCA实现人脸识别的原理及步骤:
1、样本训练
(1)图像向量化。把P张大小为的2D样本图像转化为1D列向量(或行向量)所有列向量组成矩阵sam(大小为行,即个维度,P列,即P个样本)。
(2)均值标准化。求出每个维度的均值,组成矩阵mean,每个样本每个维度分别减去各个维度的均值,得到矩阵D。这一步的结果是将每个维度变成均值为0,为了后续处理方便。
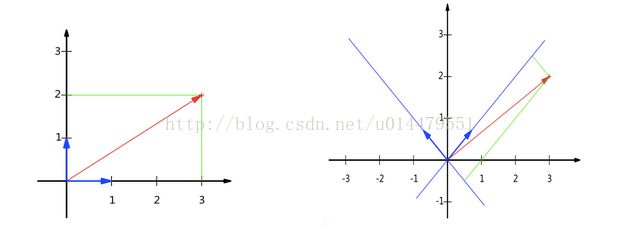
(3)求D的协方差矩阵。这一步非常关键,对其理解要很仔细。首先要清楚求协方差矩阵的目的。PCA的目的是把数据压缩,提取出最主要的信息。不同的正交基可以给同一组数据不同的表示,例如下图,以左图(1,1)为正交基,则红色的向量坐标为(3,2),右图(-1,1)为正交基,红色向量坐标为(),如果我们找到一组基来表示一组数,基的数量比数据本身的维数小,那就实现了高维数据压缩。
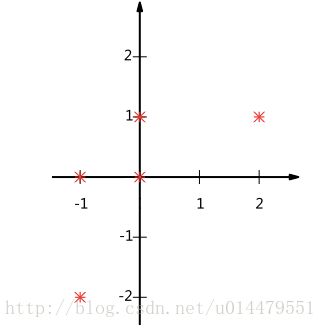
问题来了,怎么找到最优的那组正交基呢?进行数据压缩的时候,最希望压缩后的数据尽可能大地保留原数据的信息,不希望有信息丢失。例如下图,要把这五个2维数据压缩成一维,如果选X轴作为投影的基,它们投影到X轴,就有两个数据的投影值重叠(-1,0)(-1,-2)和(0,1)(0,0),投影值不知道反映原数据具体哪个,就造成信息丢失。所以,我们选正交基的时候,要使数据新基上投影后的投影值尽可能分散。
那就把问题转化到数学上了。二维数据中用方差反映分散程度,那N维数据呢?希望投影后的数据能反映原始数据信息,就是投影值之间没有相关性,反映数据间相关性的就是协方差。这里要注意的是,要考虑图像维度与维度之间的相关性,所以构造的协方差矩阵是。维数是 !!!我看到一些做法是, 最后结果也对,我搞不清楚它理论支撑何在。至于公式为什么是,几何意义可以看松子茶的博客,讲得非常清楚。
(4)求协方差矩阵的特征向量。为什么要求协方差矩阵的特征向量呢?因为协方差矩阵反映了维度与维度之间的相关性,找到协方差矩阵特征值大的前K个特征向量就是找到最优基。更详细的解释可以看松子茶的博客。由上可见协方差矩阵的维数相当高,无法直接计算协方差矩阵,及其特征向量。我就借助了SVD分解。它的原理和特征值分解差不多,这里就讲它在这步的应用吧。将偏离矩阵D进行SVD分解,U的行是的特征向量,S是特征值,V的行是的特征向量,由此我们就可以得到协方差矩阵的特征向量矩阵了。在matlab中用[U S V]=svd(D)就可以了。SVD的原理在推荐资料中可以了解到。
(5)根据上一步求到的特征值得到贡献最大的前K个特征向量(即U的前K行)。这K个特征向量就是我们要找的低维空间中的基。
(6)把每个样本向量投影到这个低维空间中。先用D与特征向量矩阵相乘,得到特征脸矩阵(),K个特征脸,再用样本向量乘以特征脸矩阵得到最后的投影值。
2、测试
(1)将待测图像转化为一维列向量
(2)与特征脸矩阵相乘得到投影值
(3)与每个样本的投影值求欧式距离
(4)判断最近的那个距离就是识别的结果
用matlab实现的结果:(人脸库来自yale)
部分特征脸:
识别结果:
小结:PCA的思想很简单,但是实际操作编程的时候,很多细节和原理要琢磨得很细,在构造协方差矩阵那停留很久,也庆幸自己敢去质疑,推敲后才得到合理的答案。