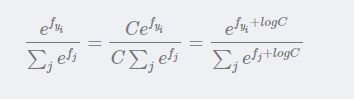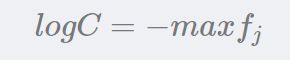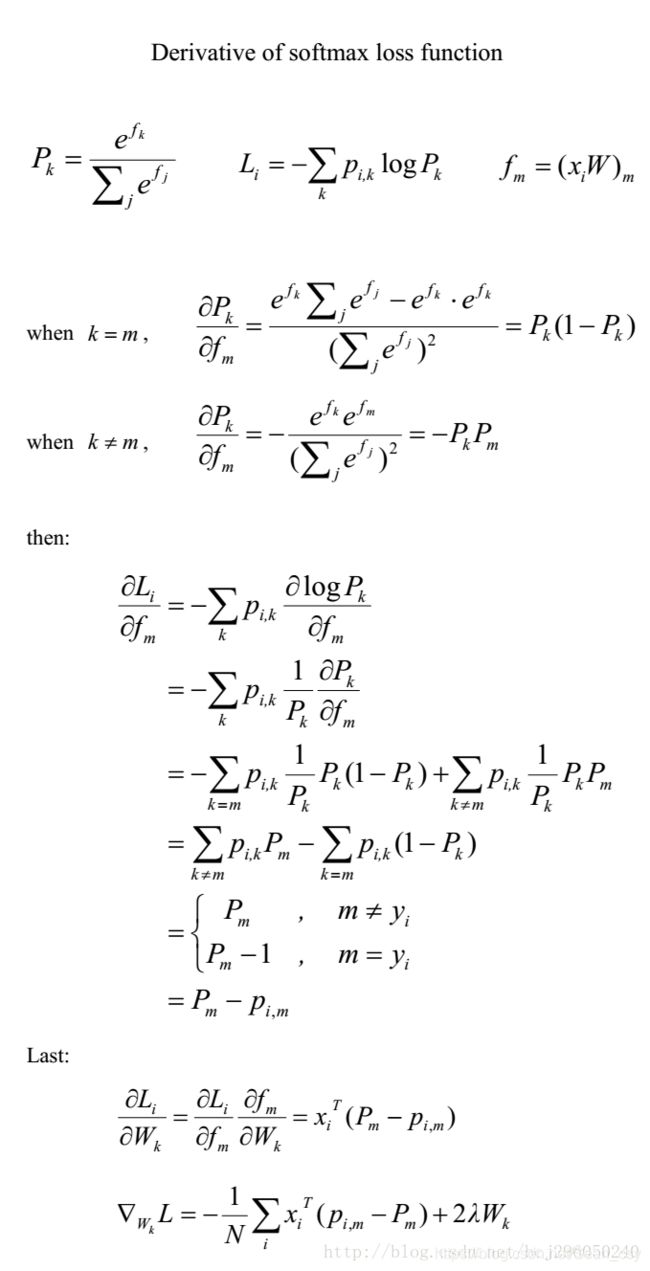cs231n assignment1_Q3_softmax
前言
其实svm和softmax的一个大区别在他们的损失函数不同,然后其梯度求导就会不同。首先,先来回顾一下softmax
softmax
所谓softmax,把它拆开看,soft & max ,可以理解为是带soft一点的max。那就会有纯max,纯max就好比一个评分函数中,得分最高的那个就是所求的分类,那么带有soft的max呢它是通过一种概率的方式,来把得分转变为概率的形式来展现,得分最高的那类自然概率也就最高,那么得分低的也存在概率,也有一定的几率能够取到,而不是很绝对的只取最高。这算是是一种softmax感性的认识。
softmax函数为
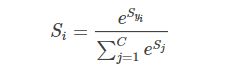
softmax的输入和svm相同,S=Wx,而它的损失函数变成了“交叉熵损失函数”(cross-entropy loss)
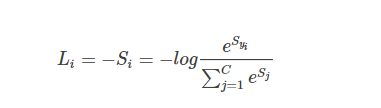
也或者写成等价形式
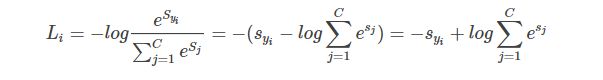
在实际使用中,常常因为指数太大而出现数值爆炸问题,两个非常大的数相除会出现数值不稳定问题,因此我们需要在分子和分母中同时进行以下处理:
其中C 的设置是任意的,在实际变成中,往往把C设置成:
即第 i 个样本所有分值中最大的值,当现有分值减去该最大分值后结果≤0,放在 e 的指数上可以保证分子分布都在0-1之内
※梯度推导(难点)
※代码实现
softmax.py
import numpy as np
from random import shuffle
from past.builtins import xrange
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
num_classes = W.shape[1]
num_train = X.shape[0]
for i in range(num_train):
scores = np.dot(X[i], W)
scores -= np.max(scores)
correct_class_score = scores[y[i]]
exp_sum = np.sum(np.exp(scores))
loss += -correct_class_score + np.log(exp_sum) # 公式
for j in range(num_classes):
if j == y[i]:
dW[:, j] += X[i] * (-1+(np.exp(scores[j]) / exp_sum)) #dL/dW=(Pk-1(Yi=k))*x
else:
dW[:, j] += X[i] * (np.exp(scores[j]) / exp_sum)
loss /= num_train
loss += 0.5 * reg * np.sum(W * W)
dW /= num_train
dW += reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW
def softmax_loss_vectorized(W, X, y, reg):
"""
Softmax loss function, vectorized version.
Inputs and outputs are the same as softmax_loss_naive.
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using no explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
num_classes = W.shape[1]
num_train = X.shape[0]
scores = np.dot(X, W)
#print(scores.shape) #(500,10)
scores -= np.max(scores, axis=1,keepdims=True) # 减去最大值防爆数
#print(scores.shape) #(500,)
#print(scores[range(num_train), y].shape) # (500,) 一维
#print(y.shape) (500,)
correct_class_scores = np.sum(scores[range(num_train), y]) #这句不怎么懂。
scores = np.exp(scores)
exp_sum = np.sum(scores, axis=1, keepdims=True) #往y轴上投影
#print(exp_sum.shape) #(500,1)
loss = -correct_class_scores + np.sum(np.log(exp_sum)) #公式 L=-Si+log()
loss = loss / num_train + 0.5 * reg * np.sum(W * W)
#根据公式 softmax求导的公式,分类讨论。
prob = scores / exp_sum
#print(prob.shape) #(500,10)
prob[range(num_train), y] -= 1 #把 -Xi 项“分配”进梯度的公式里 因为j=Yi时候,dW的结果有一项-Xi
#print(X.shape) #(500, 3073)
dW = np.dot(X.T, prob)
dW = dW / num_train + reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW
这里实现梯度求导有两个方法,一种是较傻瓜式的双重循环来求,虽然速度慢,但是比较容易理解,对求dW有个总体上的认知。第二个方法就是向量化的方法,通过矩阵的操作来进行求dW,和前面的svm的loss function求梯度一个套路。
但是,其中有句代码的语法不是特别清楚,希望哪个大佬来指点一下,代码如下:
scores[range(num_train), y]
prob[range(num_train), y]softmax.ipybn
# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of over 0.35 on the validation set.
# 用验证集来调优正则化强度和学习率。
from cs231n.classifiers import Softmax
results = {}
best_val = -1
best_softmax = None
learning_rates = [1e-7, 5e-7, 3e-7, 2e-7, 1.5e-7, 1.75e-7]
regularization_strengths = [2.5e4, 3.5e4, 5e4, 3e4, 2.75e4, 3.25e4]
################################################################################
# TODO: #
# Use the validation set to set the learning rate and regularization strength. #
# This should be identical to the validation that you did for the SVM; save #
# the best trained softmax classifer in best_softmax. #
################################################################################
for lr in learning_rates:
for reg in regularization_strengths:
softmax = Softmax()
softmax.train(X_train, y_train, lr, reg, num_iters = 600)
acc_train = np.mean(y_train == softmax.predict(X_train))
acc_val = np.mean(y_val == softmax.predict(X_val))
results[(lr,reg)] = (acc_train,acc_val)
if acc_val > best_val :
best_val = acc_val
best_softmax = softmax
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)这里就是用验证集来调优超参数的过程了