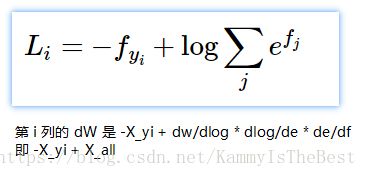【学习笔记】cs231n-assignment1-Softmax
前言
大家好,我是Kay,小白一个。以下是我完成斯坦福cs231n-assignment1-Softmax 这份作业的做题过程、思路、踩到的哪些坑、还有一些得到的启发和心得。希望下面的文字能对所有像我这样的小白有所帮助。
Softmax 与SVM 类似,区别只在于 SVM 使用的是一个 hinge loss 函数,而 Softmax 使用的是 cross-entropy loss 函数,应用思想与贝叶斯公式有异曲同工之处。
TODO1:完成两层循环的softmax
【思路】函数本身按着公式的步骤来就行:求出第i 张图片对应所有标签的分数然后做 e 取幂,把正确的标签分数当分子、分数总和做分母,最后做log 运算取负。
要注意一点的是!分母是e 取幂再总和的话,可能数值太大会爆掉,这里用到一个小技巧,分子分母同时减去同一个数(这里是减最大的数),分数仍然不变。
重复一遍:求Wx、减最大值、做e取幂、求总和、求分数、做 log 取负。
而求梯度dW,则要用到链式法则得到 dW = -X_yi + X_all
2018.7.21
上面的公式对了,但是结果错了。
dW=dL,所以要对所有的 j 做链式法则,如果 j 恰好是 yi,那 Lj = -Xj + prob * Xj;否则 Lj = prob * Xj。
所以,dL = sum(dLj) = -X[yi] + prob * X[all]
num_classes = W.shape[1]
num_train = X.shape[0]
for i in range(num_train):
scores = np.dot(X[i], W)
scores -= np.max(scores)
correct_class_score = scores[y[i]]
exp_sum = np.sum(np.exp(scores))
loss += -correct_class_score + np.log(exp_sum)
for j in range(num_classes):
dW[:, j] += X[i]
if j==y[i] :
dW[:, j] -= X[i]
loss /= num_train
loss += 0.5 * reg * np.sum(W * W)
dW /= num_train
dW += reg * W
【开始 Debug】loss 对了,但是 dW不对,这里找了好多求梯度公式的资料,查得越多,莫名其妙的符号就越多(比如 p(i,k) 是什么鬼哦!)最终决定自己手算下,发现原来是X_all 还得再乘上一个贝叶斯才行。
【修改代码】
dW[:,j]+= X[i] * (np.exp(scores[j]) / exp_sum)
梯度正确。
【思考提升】
我发现我对SVM 的梯度计算的思考上有错误!正确的 dW 是靠这张图去思考计算出来的。
TODO2:用向量方式重写softmax
【思路】广播!注意形状即可。
num_classes = W.shape[1]
num_train = X.shape[0]
scores = np.dot(X, W)
scores -= np.max(scores, axis=1, keepdims=True) #减去最大值防爆数
correct_class_scores = np.sum(scores[range(num_train), y])
scores = np.exp(scores)
exp_sum = np.sum(scores, axis=1, keepdims=True)
loss = -correct_class_scores + np.sum(np.log(exp_sum))
loss = loss / num_train + 0.5 * reg * np.sum(W * W)
prob = scores / exp_sum
prob[range(num_train), y] -= 1 #把 -Xi 项“分配”进梯度的公式里
dW = np.dot(X.T, prob)
dW = dW / num_train + reg * W结果正确。
TODO3:超参数调优
【思路】和SVM 的调参方法是一样的,用一个字典,让 (lr, rs) 去对应(acc_train, acc_val),准确率的求法则是:预测标签/正确标签。
learning_rates = [1e-7, 5e-7, 3e-7, 2e-7, 1.5e-7, 1.75e-7]
regularization_strengths = [2.5e4, 3.5e4, 5e4, 3e4, 2.75e4, 3.25e4]
for lr in learning_rates:
for reg in regularization_strengths:
softmax = Softmax()
softmax.train(X_train, y_train, lr, reg, num_iters=600)
acc_train = np.mean(y_train == softmax.predict(X_train))
acc_val = np.mean(y_val == softmax.predict(X_val))
results[(lr, reg)] = (acc_train, acc_val)
if acc_val > best_val:
best_val = acc_val
best_softmax = softmax
总结
如果说SVM 的训练的难点我是放在了“对广播使用的精进”的话,Softmax 的难点我认为就是在对dW 的计算上了。在查找资料的过程中,我认为我对于那种很硬核的“全英文+专业新知识”的文章依然还是存在强烈的抵触心理,这种心态一定要改变!不然的话以后在有DDL 的重压下,看论文啊、学习新东西的时候会更抵触更难受!
最后再吐槽一下这个文本编辑器,一点都不好用,各种混乱的缩进、空行,尤其是 ctrl+Z 简直就是谜一样的判定???