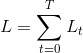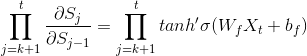【NLP】LSTM总结记录

目录

前言

RNN

梯度消失和梯度爆炸

梯度裁剪

relu、leakyrelu等激活函数

Batch Normalization(批规范化)

残差结构

LSTM（长短期记忆网络）

LSTM形式

理解LSTM结构

梯度爆炸和消失的解决

pytorch中的LSTM

参数的估计

GRU

---

前言

如果有一天，你发现有大佬会看你写的东西，你会感觉一切的一切都变得有意义吗？好比一个资质极差的凡人，终于发现自己可以凭借后天的极限奋斗，能有希望入道成仙，因而欢喜无尽呢？希望未来的那么一天，也有人会跟我说一句：吾道不孤也！借此文感谢boss上跟我聊过的这位大佬！

这篇文章写一些关于LSTM的总结。

RNN

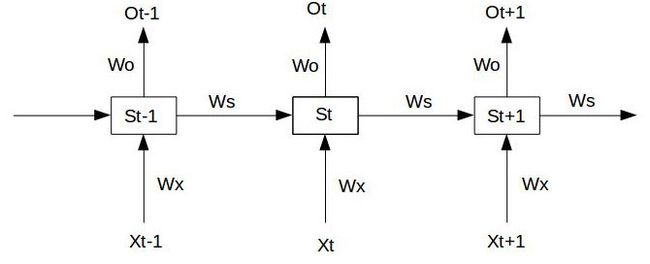
为了更加好的建模一些序列化信息，比如文本，语音，我们有了RNN（Recurrent Neural Network）。在绝大多数文章中，他长这个样子：

 

 

如上图所示，为什么他可以 建模序列化的信息呢？因为RNN每次都会将前一次的输出结果，带到下一次的隐藏层中，一起训练。前面所有时刻的输入都对未来的输出产生影响。

若时刻隐藏层 接受上一个时刻的隐藏层，我们将这种RNN叫 Elman network，若  接受上一个时刻的输出,我们称这种RNN叫Jordan network。【维基百科】

 

 

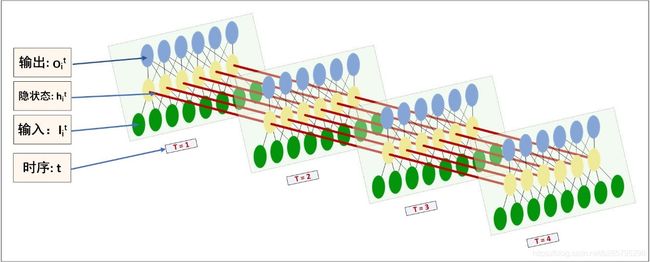
实际上，上面的图，不是很能辅助理解RNN的工作状态。借助一个例子，引自【知乎】。先看图：

 

如果有一条长文本，我给句子事先分割好句子，并且进行tokenize, dictionarize,接着再由look up table 查找到embedding，将token由embedding表示，再对应到上图的输入。流程如下：

step1, raw text:
接触LSTM模型不久，简单看了一些相关的论文，还没有动手实现过。然而至今仍然想不通LSTM神经网络究竟是怎么工作的。……

step2, tokenize (中文得分词):
sentence1: 接触 LSTM 模型 不久 ，简单 看了 一些 相关的 论文 ， 还 没有 动手 实现过 。
sentence2: 然而 至今 仍然 想不通 LSTM 神经网络 究竟是 怎么 工作的。
……

step3, dictionarize:
sentence1: 1 34 21 98 10 23 9 23
sentence2: 17 12 21 12 8 10 13 79 31 44 9 23
……

step4, padding every sentence to fixed length:
sentence1: 1 34 21 98 10 23 9 23 0 0 0 0 0
sentence2: 17 12 21 12 8 10 13 79 31 44 9 23 0
……

step5, mapping token to an embeddings:
sentence1:

 ,每一列代表一个词向量，词向量维度自行确定；矩阵列数固定为time_step length。
sentence2:
……

step6, feed into RNNs as input:

假设 一个RNN的time_step 确定为 ,则padded sentence length(step5中矩阵列数)固定为 ,--这是句子的padding操作，一次RNNs的run只处理一条sentence。每个sentence的每个token的embedding对应了每个时序  的输入。一次RNNs的run，连续地将整个sentence处理完。

step7, get output:
看图，每个time_step都是可以输出当前时序  的隐状态 ；但整体RNN的输出 是在最后一个time_step   时获取，才是完整的最终结果。

step8, further processing with the output:
我们可以将output根据分类任务或回归拟合任务的不同，分别进一步处理。

 

梯度消失和梯度爆炸

RNN模型训练的一大难题是梯度消失和梯度爆炸问题。产生梯度消失和梯度爆炸是由于RNN的权值矩阵循环相乘导致的。下面给出RNN梯度消失和爆炸的解释，该部分引自【《RNN梯度消失和爆炸的原因》-沉默中的思索-知乎】

我们拿一个三个时刻的序列处理过程来举例， 为给定值。

RNN最简单的前向传播过程如下：

假设在t=3时刻，损失函数为。

则对于这一次训练任务的损失函数为。

使用随机梯度下降法训练RNN其实就是对 求偏导，并不断调整它们以使L尽可能达到最小的过程。我们只对t3时刻的  求偏导（其他时刻类似）：

可以看出对于  求偏导并没有长期依赖，但是对于  求偏导，会随着时间序列产生长期依赖。因为 随着时间序列向前传播，而 又是   的函数。

根据上述求偏导的过程，我们可以得出任意时刻对  求偏导的公式：

任意时刻对求偏导的公式同上。

如果加上激活函数，，则

因为 ，如果中的值也是大于0小于1的值，则当t很大时 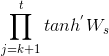，接近于0.

如果中的值很大时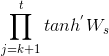，接近于无穷，这就是RNN中梯度消失和爆炸的原因。

 

梯度裁剪

避免梯度爆炸可以采用梯度截断的方法。所谓梯度截断是指将梯度值超过阈值的梯度降到阈值以内。虽然梯度截断会一定程度上改变梯度的方向，但梯度截断的方向依旧是朝向损失函数减小的方向。

from torch.nn.utils import clip_grad_norm

def clip_gradient(optimizer, grad_clip):
    """
    Clips gradients computed during backpropagation to avoid explosion of gradients.

    :param optimizer: optimizer with the gradients to be clipped
    :param grad_clip: clip value
    """
    for group in optimizer.param_groups:
        for param in group["params"]:
            if param.grad is not None:
                param.grad.data.clamp_(-grad_clip, grad_clip)# 将梯度限制在(-grad_clip, grad_clip)内

 

我们还可以通过以下一些方法缓解梯度消失和梯度爆炸

relu、leakyrelu等激活函数

relu，在小于0的时候梯度为0，大于0的时候梯度恒为1，这样使得每层的网络得到的梯度更新速度都一样。

relu的主要贡献：解决了梯度消失和梯度爆炸的问题，计算方便计算速度快(梯度恒定为0或1)加速了网络的训练

但由于负数部分恒为0，导致一些神经元无法激活(可通过设置小学习率部分解决)且输出并不是零中心化的

leakyrelu就是为了解决relu的0区间带来的影响，在小于0的区间，梯度为很小的数(非零)，leakyrelu解决了0区间带来的影响，而且包含了relu所有优点。

Batch Normalization(批规范化)

BN通过对每一层的输出归一化为均值和方差一致的方法，消除了 过大过小带来的影响，也可以理解为BN将输出从饱和区拉到了非饱和区(比如Sigmoid函数)。

残差结构

。。。

---

 

LSTM也是为了解决梯度消失或爆炸问题。换句话说，它可以解决RNN的长期依赖问题。再换句话说，他可以拥有较RNN更长的序列信息学习能力。

 

LSTM（长短期记忆网络）

而LSTM之所以能够解决RNN的长期依赖问题，是因为LSTM引入了门（gate）机制用于控制特征的流通和损失。

LSTM形式

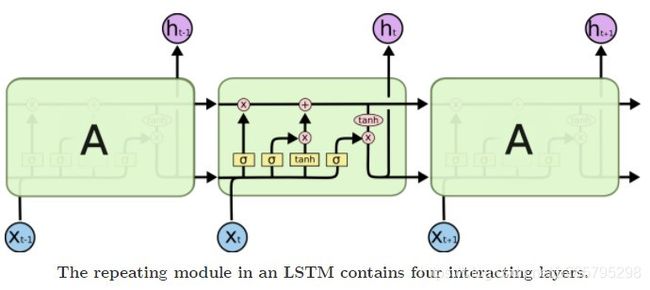
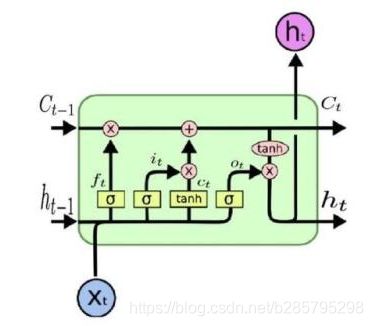
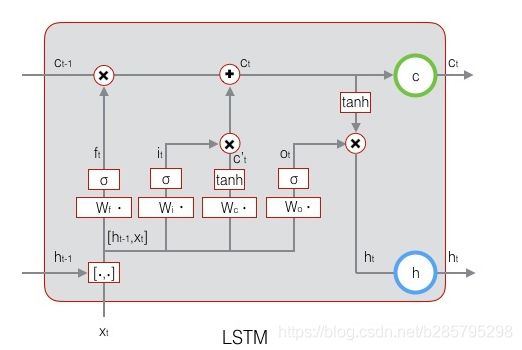
绝大部分文章中，LSTM长这个样子：

结合之前的RNN结构看，它说明了在每一个时刻，隐藏层都经过了几个特殊的运算（门的运算），然后将信息往后传递。每一个cell的具体信息如图：

各个门（f：遗忘门，i：输入门，o：输出门）的计算方式如下： 

 

 

理解LSTM结构

 称作”cell state“，他是让梯度随着时间的流动不发生指数级消失或者爆炸的关键。也是LSTM保持长期记忆的关键部件。我们之前分析了，传递过程中，隐藏层权重值的变化是导致梯度消失或爆炸的原因之一。

考虑极端的条件，如果信息在传递过程中，不加以权重。那么我们可以用  来输送信息，而无需考虑梯度的消失或爆炸。

当然，我们不能单纯这样做，我们在 的基础上，进行每一个 的信息加减。具体来说，在 时刻，是用遗忘门  与 前一个cell state  作Hadamard product（按元素相乘），然后用输入门   与当前 cell  作Hadamard product ，然后两者求和。

我们发现，计算式中，遗忘门，输入门，输出门都是 的拼接参与运算，然后用sigmoid激活， 是上一时刻的隐藏状态输出（短时记忆）。sigmoid的输出是在0-1之间的。这意味着， 的时候相当于将 的信息作了部分舍弃，我想这也就是他被称作"遗忘门"的原因。 同理  计算出需要有选择性增添的信息。两者求和，就完成了信息的忘记和增加。

输出也是一样的，用 将当前的cell state 约束回 ,然后以 的方式进行有选择的输出。相当于对积累的记忆进行了挑选。

 

梯度爆炸和消失的解决

还记得之前RNN反向传播的计算公式吗？

。

其中，，由于中值的不同，最终导致，梯度消失或爆炸。

 

我们将LSTM抽象成这样：

分别表示三个门， 表示sigmoid函数。他的值是介于0到1之间的，刚好用趋近于0时表示流入不能通过gate，趋近于1时表示流入可以通过gate。

当前的状态 ，展开后得：

最后加上激活函数：

那么，在LSTM中:

,

 的图像如下：

 图像：

 的值是【0，1】的，所以

这样就解决了传统RNN中梯度消失的问题。

 

pytorch中的LSTM

详细API 请参考：pytorch 官方文档链接

结合图示（上面RNN的展示图），我们知道，定义一个RNN，需要告诉他输入的向量长度（拿上面文本处理举例，即指定padding 后的 sentence length），隐藏层的节点数量，RNN堆叠的层数，默认是1层。

其他一些参数解释如下：

Parameters

• input_size – The number of expected features in the input x

• hidden_size – The number of features in the hidden state h

• num_layers – Number of recurrent layers. E.g., setting num_layers=2 would mean stacking two LSTMs together to form a stacked LSTM, with the second LSTM taking in outputs of the first LSTM and computing the final results. Default: 1

• bias – If False, then the layer does not use bias weights b_ih and b_hh. Default: True

• batch_first – If True, then the input and output tensors are provided as (batch, seq, feature). Default: False

• dropout – If non-zero, introduces a Dropout layer on the outputs of each LSTM layer except the last layer, with dropout probability equal to dropout. Default: 0

• bidirectional – If True, becomes a bidirectional LSTM. Default: False

 

一个示例： 

#定义一个LSTM你需要定义输入的向量长度，隐藏节点数量，和LSTM堆叠的层数。

rnn = nn.LSTM(10, 20, 2) # 一个单词向量长度为10，隐藏层节点数为20，LSTM有2层
input = torch.randn(5, 3, 10) # 输入数据由3个句子组成（batch），每个句子由5个单词组成，单词向量长度为10
h0 = torch.randn(2, 3, 20) # LSTM层数*方向为2*1， batch为3， 隐藏层节点数为20
c0 = torch.randn(2, 3, 20) # 同上
output, (hn, cn) = rnn(input, (h0, c0))

print(output.shape, hn.shape, cn.shape)

>>> torch.Size([5, 3, 20]) 
torch.Size([2, 3, 20]) torch.Size([2, 3, 20])

可以发现，定义好LSTM之后， 我们需要初始化 ，pytorch 中两者默认初始化输入方式为：（nlayers* direction , batch_size , hidden），如之前例子所述，LSTM一次会跑完整个句子，output 在最后一个时刻跑完后产生，他实际上是包含所有时刻hidden的tensor，维度为[sequence_length *  batch_size * hidden_size]。hn,cn在每一个时刻都会产生。

参数的估计

 

LSTM参数个数与无关。如图，我们可以看到，涉及到的参数都在 四步的运算中。输入都是 的拼接，计算后输出的 与  等维度。

那么假设输入 的维度为 X , 隐藏层维度为 H,那么 参数矩阵的维度应该为（X+H）* H,  四步的运算的操作都可简化为,   的维度显然是 H * 1 ,于是总参数为：4 * （（X+H）* H + H）

GRU

GRU（Gate Recurrent Unit）是循环神经网络（Recurrent Neural Network, RNN）的一种。和LSTM（Long-Short Term Memory）一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。相比LSTM，使用GRU能够达到相当的效果，并且相比之下更容易进行训练，能够很大程度上提高训练效率。

GRU结构如下：

GRU的两个门，分别是reset gate  和 update gate  计算方法和LSTM中门的计算方法类似。 选隐藏层（candidate hidden layer） 相当于LSTM 中的  ，  控制信息的保留，最后  控制需要从前一时刻的隐藏层 中遗忘多少信息，需要加入多少当前 时刻的隐藏层信息 。

 

 

参考文献：

1. Chung J, Gulcehre C, Cho K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J]. arXiv: Neural and Evolutionary Computing, 2014.
2. Understanding LSTM Networks
3. https://en.wikipedia.org/wiki/Long_short-term_memory
4. https://zhuanlan.zhihu.com/p/28687529
5. https://pytorch.org/docs/stable/nn.html?highlight=lstm#torch.nn.LSTM