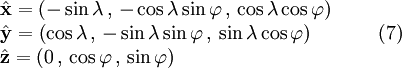Transformations between ECEF and ENU coordinates
Note:本文假设ecef和enu坐标原点相同,则两者之间只有旋转关系。
若ecef坐标原点和enu坐标原点不同,则两个坐标系之间还要加上平移量。
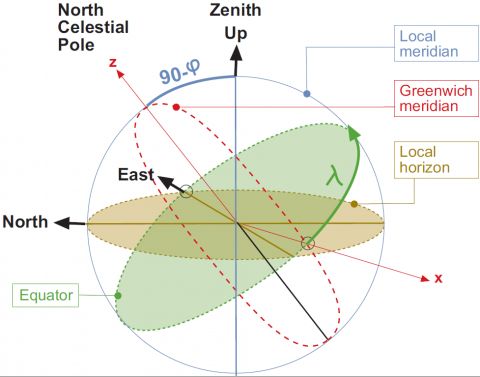
The relation between the local East, North, Up (ENU) coordinates and the (x,y,z) Earth Centred Earth Fixed (ECEF) coordinates is illustrated in the next figure:
(补充两张图,便于理解地心维度、大地维度以及下面的从enu到ecef的旋转关系)
From the figure 2 it follows that the ENU coordinates can be transformed to the (x,y,z) ECEF by two rotations:
-
1. A clockwise rotation over east-axis by an angle
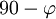 to align the up-axis with the
z-axis. That is
to align the up-axis with the
z-axis. That is
![{\mathbf R}_1[-(\pi/2-\varphi)]](http://img.e-com-net.com/image/info8/7b573223b36c482f9629efe81c979860.png) .
.
-
2. A clockwise rotation over the
z-axis by and angle
90 + λ to align the east-axis with the
x-axis. That is
![{\mathbf R}_3[-(\pi/2+\lambda)]](http://img.e-com-net.com/image/info8/431bee5589ca480c8469fe18a61913a8.png) .
.
That is:
where, according to the expressions (2) (see Transformation between Terrestrial Frames)
yields:
The unit vectors in local East, North and Up directions as expressed in ECEF cartesian coordinates are given by the columns of matrix (3). That is:
Note: If ![]() are ellipsoidal coordinates, thence, the vector
are ellipsoidal coordinates, thence, the vector ![]() is orthogonal to the tangent plane to the ellipsoid, which is defined by
is orthogonal to the tangent plane to the ellipsoid, which is defined by ![]() . If
. If ![]() are taken as the spherical latitude and longitude, thence, the vector
are taken as the spherical latitude and longitude, thence, the vector ![]() is in the radial direction and
is in the radial direction and ![]() defines the tangent plane to the sphere.
defines the tangent plane to the sphere.
From ECEF to ENU coordinates
Taking into account the properties of the rotation matrices ![]() ,i.e.,
,i.e., ![]() , thence, the inverse transformation of (1) is given by:
, thence, the inverse transformation of (1) is given by:
where the transformation matrix of (5) is the transpose of matrix (3):
The unit vectors in the ECEF ![]() ,
, ![]() and
and ![]() directions, as expressed in ENU coordinates, are given by the columns of matrix (6). That is:
directions, as expressed in ENU coordinates, are given by the columns of matrix (6). That is:
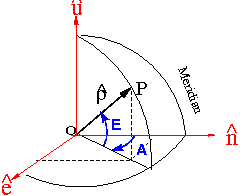
Elevation and azimuth computation
Given the line of sight unit vector
where ![]() and
and ![]() are the geocentric position of the satellite and receiver, respectively, the elevation and azimuth in the local system coordinates (ENU), defined by the unit vectors
are the geocentric position of the satellite and receiver, respectively, the elevation and azimuth in the local system coordinates (ENU), defined by the unit vectors ![]() ,
, ![]() and
and ![]() can be computed from (see figure 2):
can be computed from (see figure 2):
Thence the elevation and azimuth of satellite in the local coordinates system are given by:
Note: If ![]() are ellipsoidal coordinates, thence, the vector
are ellipsoidal coordinates, thence, the vector ![]() is orthogonal to the tangent plane to the ellipsoid, which is defined by
is orthogonal to the tangent plane to the ellipsoid, which is defined by ![]() . If
. If ![]() are taken as the spherical latitude and longitude, thence, the vector
are taken as the spherical latitude and longitude, thence, the vector ![]() is in the radial direction and
is in the radial direction and ![]() defines the tangent plane to the sphere.
defines the tangent plane to the sphere.
From:http://www.navipedia.net/index.php/Transformations_between_ECEF_and_ENU_coordinates
![\left [\begin{array}{l}x\\y\\z\\\end{array}\right ] ={\mathbf R}_3[-(\pi/2+\lambda)]\,{\mathbf R}_1[-(\pi/2-\varphi)]\left [\begin{array}{l}E\\N\\U\\\end{array}\right ]\qquad \mbox{(1)}](http://img.e-com-net.com/image/info8/0dd0023f1f464d4f9e3db1058ef186c6.png)
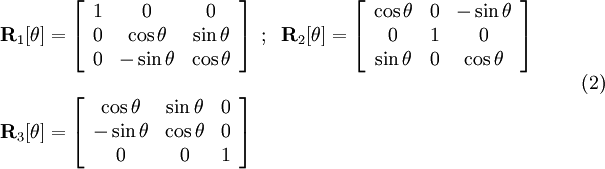
![{\mathbf R}_3[-(\pi/2+\lambda)]\,{\mathbf R}_1[-(\pi/2-\varphi)]=\left (\begin{array}{ccc}-\sin \lambda & -\cos \lambda \sin \varphi &\cos \lambda \cos \varphi\\\cos \lambda & -\sin \lambda \sin \varphi & \sin \lambda \cos \varphi\\0 & \cos \varphi & \sin \varphi\\\end{array}\right )\qquad \mbox{(3)}](http://img.e-com-net.com/image/info8/9afa7e8ddc1248d3bafb6bb67cdd8f3a.png)
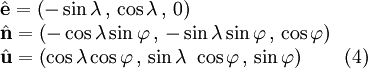
![\left [\begin{array}{l}E\\N\\U\\\end{array}\right ] ={\mathbf R}_1[\pi/2-\varphi]\,{\mathbf R}_3[\pi/2+\lambda]\left [\begin{array}{l}x\\y\\z\\\end{array}\right ]\qquad \mbox{(5)}](http://img.e-com-net.com/image/info8/3e4bcfa2c90942e0904b1a5b7b30c35b.png)
![{\mathbf R}_1[\pi/2-\varphi]\,{\mathbf R}_3[\pi/2+\lambda]=\left (\begin{array}{ccc}-\sin \lambda & \cos \lambda &0\\- \cos \lambda \sin \varphi & -\sin \lambda \sin \varphi & \cos \varphi\\\cos \lambda \cos \varphi & \sin \lambda \cos \varphi & \sin \varphi\\\end{array}\right )\qquad \mbox{(6)}](http://img.e-com-net.com/image/info8/6eb1353ff8bb487bb1ef8434518f9e36.png)