给定n位正整数a，去掉其中任意k个数字后，剩下的数字按原次序排列组成⼀个新的正整数，求组成的新数最小的删数方案（O((n-k)logk)优化）

问题描述

给定n位正整数a，去掉其中任意k个数字后，剩下的数字按原次序排列组成⼀个新的正整数。对于给定的n和k，设计⼀个算法，找出剩下数字组成的新数最少的删数方案。

这一道题来自zyq老师的算法分析与设计实验当中，因为做完以后发现网上没有类似方法的题解，于是索性上来CSDN发一篇。

没错老师，这句话就是给您看的，这里的题解是从实验报告中拿出来发到CSDN的，而不是先有了网上的题解再抄到实验报告，博客上的插图也是从展示PPT上截的（认真）。

解题思路

可采取贪心算法求解。显然高位数位的数值大小更对数字的大小起决定性作用，因此从高位开始贪心，挑选小数字数位保留。

简单贪心删k法

简单贪心删k法的思路是从高位往低位贪心，当当前可删k个数时，选取前k+1个高位，找到最小数（有多个最小则优先选定靠左高位数），该最小数即保留数位，该位的左方数字删去，算法流程如下：

若某轮有删除配额k：

1.选取最左k+1个数组成的子序列；

2.在子序列中选取最小数值；

3.消耗删除配额，将最小值左方数位从原序列删去（若有多最小值，选取靠左数位）（k->k’，剩余可删数位数减少）；

4.将选定的最小数值数位移出原序列，输出到答案序列中；

5.If 剩余序列长度 == k’（下一轮不足以选取k’+1个数）

直接将剩余序列全部删去；

   Else if k’ == 0（无剩余删除配额）

剩余序列全部保留，输出到答案序列中。

例： 设有10位数字a = 7519385410，删除配额k = 5 从左搜索高位前6个，子序列为751938，最小数值为1，选定1，删掉75，k=k-2=3，已有答案序列为1 从左搜索高位前4个，子序列为9385，最小数值为3，选定3，删掉9，k=k-1=2，已有答案序列为3 从左搜索高位前3个，子序列为854，最小数值为4，选定4，删掉85，k=k-2=0，已有答案序列为134 k == 0，剩余序列全部保留，得到最终解13410。

该法最好情况为前k+1个数位数值单调递减，一轮搜索删除k个数得出结果，时间复杂度O(k+1)；最坏情况为单调不递减序列，每轮搜索均直接保留最高位，需搜索n-k轮，每轮搜索k位，时间复杂度O(k(n-k))。代码如下：

//全CSDN最菜。GitHub: Catigeart

/*
思路：从高位到低位贪心删掉k个数。
每轮先搜索宽度为删除数量+1的数列窗口，保留其中最小数值数位（如有多个最小值，保留高位最小值）
删去最小数值数位左方数位，窗口长度减去已删去数量，移动到最小数值数位右方继续贪心
若删除配额用完，余下的数位直接保留； 
 
例子：设有10位数字，7519385410，删5个。 
搜索前6个，751938，删掉75，1为保留位
9385410中搜索9385，删9，3为保留位
搜索854，删85，4为保留位
已无删除配额，余下数位直接保留，13410即为所求

若余下数位与删除配额相等，余下全部删去。

例子：12345，删2个，保留123后45删去。 

最坏情况下为前n-k个数字不递减排列，如此一直保留最左方数位而不删除，逐位移动窗口， 
窗口长度恒为k+1，每回线性遍历k+1，因此最坏时间复杂度为O(n*(n-k+1))=O(n^2)。

最好情况搜索第一遍即删去k个，O(k+1)。 
*/

#include
#include

#define MAXN 100000000

using namespace std;

char n[MAXN];//use char to avoid error cause by 0 at the end
char ans[MAXN];//answer char[]
int np, ap;//pointer of n[],ans[]

int main()
{
    int k;
    printf("Please input n:");
    scanf("%s",n);//save in char[] to get digit
    int nlen = strlen(n);
    if(n[0]=='-' || (nlen==1 && n[0]=='0'))
    {//invalid input n
        printf("n isn't a positive integer!\n");
        return 0;
    }
    printf("Please input k:");
    scanf("%d",&k);
    if(nlen <= k)
    {//invalid input k
        printf("No enough number !\n");
        return 0;
    }
    int Min, p;//p used as pointer
    while(k!=0 && nlen-np>k)
    {//k is the width of searching window
        p = np;
        Min = n[p];
        for(int i=np+1; i-np<=k; i++)
        {//linear traverse to get Min digit
            if(Min > n[i])
            {
                Min = n[i];
                p = i;
            }
        }
        ans[ap] = n[p];
        ap++;//ap point to the next digit
        k = k-(p-np);//k - (the number of deleted digits)
        np = p+1;//for p is kept in ans[], np should point to the next one
    }
    if(nlen-np <= k)
        np = nlen;//delete lasted digits
    while(n[np] != 0)
    {//if still digits lasted, keep them directly
        ans[ap] = n[np];
        ap++;
        np++;
    }
    ap = 0;//reset ans point 
    if(ans[ap] == '0')
    {
    	printf("(");
    	while(ans[ap] == '0')
    	{
    		printf("%c",ans[ap]);
    		ap++;
		}
    	printf(")");	
	}
	while(ans[ap])
	{
		printf("%c",ans[ap]);
    	ap++;
	}
    return 0;
}

优化潜力：锦标赛优化

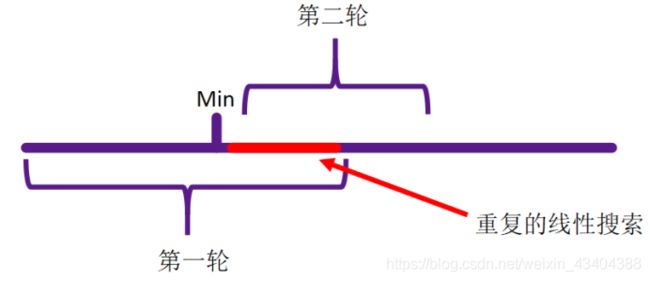
然而，该法仍然有优化空间，如下图所示：

如上图所示，在上一轮到本轮搜索之前，可能存在重复的线性搜索，若能找到记录已搜索信息的方法，则算法可以得到优化。此处采用锦标赛算法进行优化。锦标赛算法介绍参考博客：https://www.cnblogs.com/james1207/p/3323115.html

对于完全的锦标赛排序算法而言（从第1小一直求到第k小）需要构造树实现，而如果只是求少数几个排序，一个简化的编码方案只需对每个数附加一个败者列表即可（参考屈婉玲《算法分析与设计》分治章求第二大（小）思路）。

首先，锦标赛算法成对对决，并且胜者记录下被其打败的对手，最终找到第一小。

若我们从k个数中找到第一小，则第一小打败logk个对手。显然，若我们要找第二小，第二小必然在被第一小直接击败的列表中去找，若不被直接击败，则其至少是第三小。因此线性k遍历以后，只需O(logk)复杂度便可找到第二小。

同理，第二小打败logk-1个对手，第三小要么被第一小击败，要么被第二小击败，则只需约两遍O(logk)便可找到第三小。

……

参考以上思路，我们发现，把Min选取以后，可以在Min的【右方】（左方的数已经被删掉了！）搜索第二小作为浓缩后的信息传递给下一轮，这样下一轮比赛中只需和该第二小比较便可知道下一轮的第一小是否出现在重复数列中。

贪心删k法+锦标赛优化

设某轮有删除配额k：

1. 将原方法的子序列中的与上一轮搜索的子序列重复的部分剪去（代码实现方式为：若上一轮未找出Min右方的最小数位LastMin（即无重复序列），则子序列不予裁剪），即子序列左端为上一轮窗口右端+1。

2.（分治）锦标赛算法分组比较，各自记录被直接击败的数位，求出子序列的第一小tmpMin；

3.消耗删除配额，将最小数值左方数位从原序列删去（若有多最小值，选取靠左数位）（k->k’，剩余可删数位数减少）

4.若LastMin存在，将本轮第一小tmpMin与上轮LastMin比较，败者加入胜者的败者列表，胜者成为Min

5.在败者列表中找到本轮的（右方）第二小SecondMin （若有多最小值，选取靠左数位）。

6.将Min和SecondMin的位于Min左方的败者数位删去，将Min的败者列表“挂靠”到SecondMin的败者列表上，SecondMin即向下一轮传递的LastMin。即向下一轮传递的败者信息同时包括第一小和第二小的右方败者信息；

7.将位置位于Min左方的败者数位从败者列表中去除（已被删去），从剩余数位中找出最小，即（右方）第二小SecondMin；

8.将选定的最小数值数位移出原序列，输出到答案序列中；

9.If 剩余序列长度 == k’（下一轮不足以选取k’+1个数）

直接将剩余序列全部删去；  

 Else if k’ == 0（无剩余删除配额）     剩余序列全部保留，输出到答案序列中。

10.将SecondMin及其败者信息（包括Min和Second的败者信息）向下一轮传递，成为下一轮的LastMin。

为什么要向下一轮传递第一小和第二小的右方败者信息？这是因为若上轮第二小比新的数列部分任何一个数都要小，那么本轮的第二小就要从重复数列部分查找，而在上轮，重复数列的第一小和第二小都已经被找出了，那么这时候我们实际找的是第三小数，因此总共要查两轮O(logk)！

例：设有10位数字a = 7519385410，删除配额k = 5

从左搜索高位前6个，子序列为751938，最小数值为1，选定1，删掉75，k=k-2=3，已有答案序列为1，938中找到最小值3（第二小），将3及1,3的1右方败者信息向下一轮传递；

从左搜索高位前4个，子序列为9385，剪裁重复部分后剩下5，5与3比较，最小数值为3，选定3，删掉9，k=k-1=2，已有答案序列为13，85中找到最小值5，将5及5,3的3右方败者信息向下一轮传递；

从左搜索高位前3个，子序列为854，剪裁后重复部分剩下4，最小数值为4，选定4，删掉85，k=k-2=0，已有答案序列为134，4右方无序列，不传递信息；

k == 0，剩余序列全部保留，得到最终解13410。

最好情况为前k+1个数位数值单调递减，一轮搜索删除k个数得出结果，时间复杂度O(k+1)； 最坏情况单调不递减序列，在不回退的情况下总共线性遍历n-k位；两轮查败者，时间复杂度O(2logk)；总时间复杂度约为O((n-k)*2logk)=O((n-k)logk)。代码如下：

//全CSDN最菜。GitHub:Catigeart
#include
#include
#include

#define MAXN 1000000
#define LOSERN 30//log2(10^8)<27

using namespace std;

typedef struct N{
    char data;//数位值，用char存放不影响比较
    int loserPos[LOSERN];//败者列表
    int lpLen;//败者信息长度
}N;

N n[MAXN];
char ans[MAXN];
int np, ap;//num point & ans point
int k;
int player[MAXN+1];//锦标赛数组

int cmp(int nPosA, int nPosB);
void compete(int head, int rear ,int minArr[]);

int main()
{
    //初始化
    printf("Please input n:");
    char c;
    scanf("%c", &c);
    int nLen = 0;
    while(c != '\n')
    {
        n[nLen].data = c;
        nLen++;
        scanf("%c", &c);
    }
    nLen++;
    if(n[0].data=='-' || (nLen==1 && n[0].data=='0'))
    {//非法输入n
        printf("n isn't a positive integer!\n");
        return 0;
    }
    printf("Please input k:");
    scanf("%d",&k);
    if(nLen <= k)
    {//非法输入k
        printf("No enough number !\n");
        return 0;
    }
    int minPosArr[2] = {MAXN+1,MAXN+1};//minPos,2ndMinPos.MAXN+1表示空
    int deleteNum;//删除数量
    int head=0, rear=k;//搜索区域的头尾
    while(k!=0 && nLen-np>k)
    {
        compete(head, rear, minPosArr);
        deleteNum = minPosArr[0]-np;
        k -= deleteNum;//k值更新
        np = minPosArr[0]+1;//np移动
        ans[ap] = n[minPosArr[0]].data;//传值到ans数组
        ap++;//ap移动
        //若上一轮有已搜索信息向本轮传递，则裁剪区域
        if(minPosArr[1] != MAXN+1)
            head = rear+1;//cut
        else//如果==MAXN+1，即无第二小信息
            head = np;
        rear = np+k;
    }
    if(nLen-np <= k)//已不能再保留新数，按算法不会发生<情况，仅鲁棒写法
        np = nLen;//移动np到末尾，等同直接删去
    while(n[np].data != 0)
    {//如果删完了仍然有剩余数位，直接保留
        ans[ap] = n[np].data;
        ap++;
        np++;
    }
    ap = 0;//重置ap
    //前导零的特殊处理
    if(ans[ap] == '0')
    {
        printf("(");
        while(ans[ap] == '0')
        {
            printf("%c",ans[ap]);
            ap++;
        }
        printf(")");
    }
    while(ans[ap])
    {
        printf("%c",ans[ap]);
        ap++;
    }
    printf("\n");
    system("pause");
    return 0;
}

int cmp(int nPosA, int nPosB)
{//锦标赛算法比较函数
    int smallPos, bigPos;
    if(n[nPosA].datan[pos1st].loserPos[i]))
        {//若更小或等值但位置位于当前值的左方
            pos2nd = n[pos1st].loserPos[i];
            data2nd = n[n[pos1st].loserPos[i]].data;
        }
    }//pos2nd可能== MAXN+1(没有发生比较)
    if(pos2nd != MAXN+1)
    {//把pos1st的败者记录附加到pos2nd中向下一轮传递
        for(i=0; i

说实话，贪心+锦标赛以后相互指向情况有点乱，数组套娃看起来并不友好。然后其实对二叉树实现锦标赛算法没太琢磨，说不定树实现会快些。

再然后，第一次写这么长的东西，不知道会不会语无伦次，希望不会造成阅读困难（害怕.jpg）。