自动机，状态机，有限自动机，有限状态机，有限状态自动机，非确定下有限状态自动，确定性有限状态自动机的区别于联系

这几个概念晕了几天了，搞明白了就来备注一下

FSM（Finite State Machine）

FAM（Finite Automata Machine）

DFA（Determinate Finite Automata）

NFA（Non-Determinate Finite Automat）

自动机：自动机是有限状态机(FSM)的数学模型。

状态机：我们现在所说的状态机一般是有限状态机（FSM）的简称。

有限自动机： 有限自动机（Finite Automata Machine）是计算机科学的重要基石，它在软件开发领域内通常被称作有        限状态机（Finite State Machine），是一种应用非常广泛的软件设计模式（Design Pattern）。

有限状态机：

对有限状态机的定义：有限状态机是具有一个基本内部记忆的抽象机器模型，定义如下：

根据输出与输入、系统状态的关系，有限状态机又可分为Moore型有限状态机和Mealy型有限状态机

Moore型有限状态机是指输出仅与系统状态有关，与输入信号无关的状态机。优点是将输入和输出分 隔开.

Mealy型有限状态机是指输出与系统状态和输入均有关系的有限状态机。

为了直观，直接用转移图来说明两者的区别

转移图是一种有向图，由圆表示有限状态机的状态，有向曲线表示系统的状态转移过程，有向线段的起点 表示初始的状态，终点表示转移后的状态。
       

对于Mealy型有限状态机在有向曲线段上的字符表示系统的输入和输出，用“/”分隔。
         对于Moore型有限状态机，通常在状态后标出输出值，用“/”分隔，输入信号仍然在有向线段上标注。

图1： Mealy型状态机的转移图

图1所示的有限状态机只有一位输入、一位输出，两个状态A1和A2，左侧绘制的指向A1的箭头表示系统的初始状态为A1；在A1的上方，绘制一个起点和终点都在A1上的有向曲线，以及曲线上的标注“1/0”表示，当状态为A1，输入信号为1时，有限状态机的状态不变，输出为0；由A1指向A2的标注为“0/1”的箭头表示，当系统状态为A1，输入为0时，系统状态变为A2，且输出为1。同理，由转移图可知，当系统处于A2状态时，输入为1时状态不变，输出为1；当输入为0时，状态变为A1，输出为0。对于比较复杂的有限状态机，在有向箭头的标识上还可以添加字符说明。

图2： Moore型状态机转移图

图2所示的Moore型有限状态机只有一位输入、一位输出，两个状态A1和A2，左侧绘制的指向A1的箭头表示系统的初始状态为A1；标注“A1/1”表示处于状态A1时，输出为1；同理“A2/0”表示处于状态A2时，系统输出为0；在状态A1上方绘制的起点和终点均在A1上的有向曲线，以及曲线上的标注“1”表示，当状态为A1，输入信号为1时，有限状态机的状态不变；由A1指向A2的标注为“0”的箭头表示，当状态为A1，输入为0时，有限状态机的状态变为A2。当有限状态机处于A2状态时，如果输入为1，有限状态机的状态就会变为A1。 

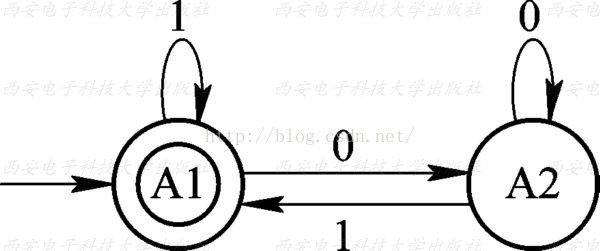
对于这种输出在{0，1}二值区间的Moore型有限状态机，一般称之为有限状态自动机，对于有限状态自动机还有另一种转移图的表示方法，即用双圆环表示输出为1的状态，并称之为接受状态。使用这种转移图画法后，图2所示的有限状态机可绘制为如图3所示的转移图。

图3：有限状态自动机

有限状态自动机：（FSM "finite state machine" 或者FSA "finite state automaton" ）是为研究有限内存的计算过程和某些语言类而抽象出的一种 计算模型。有限状态自动机拥有有限数量的状态，每个状态可以迁移到零个或多个状态，输入字串决定执行哪个状态的迁 移。有限状态自动机可以表示为一个有向图。有限状态自动机是自动机理论的研究对象。

有限状态自动机是具有离散输入和输出的系统的一种数学模型 。

其主要特点有以下几个方面：

– (1) 系统具有有限个状态，不同的状态代表不同的意义。按照实际的需要，系统可以在不同的状态下完成规定的任务。

– (2) 我们可以将输入字符串中出现的字符汇集在一起构成一个字母表。系统处理的所有字符串都是这个字母表上的字符串。

– (3) 系统在任何一个状态下，从输入字符串中读入一个字符，根据当前状态和读入的这个字符转到新的状态。

– (4) 系统中有一个状态，它是系统的开始状态。

– (5) 系统中还有一些状态表示它到目前为止所读入的字符构成的字符串是语言的一个句子。

形式定义

· 定义：有限状态自动机(FA—finite automaton)是一个五元组：

– M=(Q, Σ, δ, q0, F)

· 其中，

– Q——状态的非空有穷集合。∀q∈Q，q称为M的一个状态。

– Σ——输入字母表。

– δ——状态转移函数，有时又叫作状态 转换函数或者移动函数，δ：Q×Σ→Q，δ(q,a)=p。

– q0——M的开始状态，也可叫作初始状态或启动状态。q0∈Q。

– F——M的终止状态集合。F被Q包含。任给q∈F，q称为M的终止状态。

有限状态自动机还可以分成确定与非确定两种。非确定有限状态自动机可以转化为确定有限状态自动机。

自动机从初始状态 q0 起，逐一读入输入串（由输入字母表 Σ 的字母构成）的每一个字母，根据当前状态、输入字母和转移函数 δ 决定自动机的下一步状态；如果输入串结束时，自动机处于终结状态集合 F 的某一个状态，这表示自动机接受该字串；否则自动机不接受该字串。

非确定有限状态自动机与确定有限状态自动机的唯一区别是它们的转移函数不同。确定有限状态自动机对每一个可能的输入只有一个状态的转移。非确定有限状态自动机对每一个可能的输入可以有多个状态转移，接受到输入时从这多个状态转移中非确定地选择一个。

确定型有限状态自动机：

形式化定义：

确定有限状态自动机 是由

• 一个非空有限状态的集合 Q
• 一个输入字母表 Σ（非空有限字符的集合）
• 一个转移函数 （例如：），每一个转移都有确定的值
• 一个开始状态 
• 一个接受状态的集合 

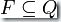
所组成的5-元组。因此一个DFA可以写成这样的形式： 。

非确定型有限状态自动机：

形式化定义：

不确定有限状态自动机 是由

• 一个非空有限状态的集合 Q
• 一个输入字母表 Σ（非空有限字符的集合）
• 一个转移函数  ，每一个转移（一个状态下，同一个输入）都几个不确定的值（次态），采取随机转移方式转移到下一个状态
• 一个开始状态 
• 一个接受状态的集合 

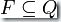
所组成的5-元组。因此一个DFA可以写成这样的形式： 。

DFA与NFA的不同就是转移函数的不同。

DFA与NFA可以相互装换，具体如何转换参考：NFA转换为DFA

总结：我们平常说的状态机其实就是指有限状态自动机，有限自动机是一套自动机理论，当被用于特定的领域之后就被称为有限状态机，而有限状态机的数学模型就是自动机。

状态机是是一个概念，一个工具。我们经常采用状态机来对事物建模，使用状态机来建模的主要学科有：

在计算机科学中自动机用作计算机和计算过程的动态数学模型，用来研究计算机的体系结构、逻辑操作、程序设计乃至计算复杂性理论。

具体应用方面：

数字电路设计

游戏开发

单片机开发

设计模式之状态机模式

状态机工作流（基于事件转移）

任何一个具有状态变化的对象或事物都可以用状态机来建模

在语言学中则把自动机作为语言识别器，用来研究各种形式语言。

在神经生理学中把自动机定义为神经网络的动态模型，用来研究神经生理活动和思维规律，探索人脑的机制。

在生物学中有人把自动机作为生命体的生长发育模型，研究新陈代谢和遗传变异。在数学中则用自动机定义可计算函数，研究各种算法。

看到一句话"根本没有输出函数的有限状态机叫做半自动机或转移系统"，那么按照有限状态自动机的定义没有输出函数难道就是半自动机吗。