"Help Jimmy" 是在下图所示的场景上完成的游戏。
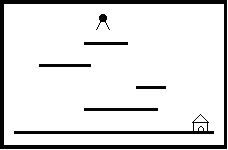
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。
Input 第一行是测试数据的组数t(0 <= t <= 20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。N是平台的数目(不包括地面),X和Y是Jimmy开始下落的位置的横竖坐标,MAX是一次下落的最大高度。接下来的N行每行描述一个平台,包括三个整数,X1[i],X2[i]和H[i]。H[i]表示平台的高度,X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000,-20000 <= X, X1[i], X2[i] <= 20000,0 < H[i] < Y <= 20000(i = 1..N)。所有坐标的单位都是米。
Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
Output 对输入的每组测试数据,输出一个整数,Jimmy到底地面时可能的最早时间。 Sample Input
1 3 8 17 20 0 10 8 0 10 13 4 14 3Sample Output
23
题解:
1.首先Jimmy是从高向低掉落,所以首先你需要将输入的板块按照高度的顺序由高到低排列,而且与其相对应的左右横坐标也需要更新
2.排序之后,思考Jimmy的位置,一开始,它的位置是一个点,那么他只可以垂直向下掉落,而且只有俩种情况
(1)直接落地(前提是这个高度要小于MAX, 不然它就摔死了)
(2)掉落到第一块板子上
3.要注意,板块不可以穿越!而且有一种边缘情况,就是你从上一块板块的边缘落下,正好落到了下一块的板块的边缘,它是可以停留的(就像之前手机上玩的游戏跳跳球一样)
4.重新回到Jimmy落到了一块板块的中央,这是先不管它, 你只需要知道它落到了哪个板块上, 并把它存储起来
5.这时我们从第一个板块说起,也就是最高的那个板块,我们来讨论从它的边缘下落问题,可以分为俩个问题, 从左边缘下落, 右边缘下落
于是可以得到(以左边缘下落为例子,右边缘相同)
if(板子k左端正下方没有别的板子){
if(板子k的高度h(k)大于MAX)
LeftMinTime(k) = INF(很大的数)
else
LeftMinTime(k) = h(k);
}
else if(板子k左端正下方的板子编号时m)//这里需要注意,仅当俩块板子的高度差小于MAX才能执行下面的语句,否则Jimmy会被摔死,则Time为INF(非常重要)
LeftMinTime(k) = h(k) - h(m) + Min(LeftMinTime(m) + Lx(k) - Lx(m), RightMinTime(m) + Rx(m) - Lx(k));
}
6.对于寻找下方是否有板子可以设置一个函数find
int find(int x, int h) {//x为Jimmy所在的横坐标,h为当前板子的高度
for (int i = 0; i < N; i++) {
if (x >= X1[i] && x <= X2[i]) {
if (h > H[i] && H[i] != 0)//这里要保证H[i]不为0,因为地面是0,树立在地面的板子是没有意义的
return i;
}
}
return -1;
}
测试数据
2 3 8 7 2 6 14 6 4 10 4 5 14 2 1 6 10 20 2 3 5 answer: 17 10 1 4 14 5 6 3 22 1 16 23 2 16 30 3 13 21 4 答案:15 1 2 2 12 8 0 10 10 2 12 5 答案:22 1 3 8 17 20 8 10 8 8 10 13 8 14 3 ans:17 1 60 822 302 50 813 823 298 813 823 293 816 826 213 816 826 178 817 827 218 813 823 148 821 831 73 814 824 248 813 823 283 815 825 158 819 829 58 814 824 13 813 823 28 819 829 233 814 824 43 773 783 293 821 831 93 818 828 268 816 826 198 818 828 113 814 824 208 816 826 68 821 831 133 794 804 248 814 824 108 829 839 28 818 828 143 844 854 298 802 812 133 801 811 28 818 828 238 817 827 8 816 826 48 820 830 3 819 829 288 822 832 138 820 830 183 855 865 13 777 787 268 820 830 63 789 799 28 822 832 33 855 865 213 779 789 208 836 846 248 806 816 33 821 831 263 818 828 83 846 856 263 789 799 68 854 864 8 854 864 283 801 811 298 805 815 143 822 832 23 821 831 173 813 823 153 858 868 138 818 828 98 839 849 133 答案:352
代码 :
1 #include2 #include 3 #include 4 using namespace std; 5 6 static const int MAXLEN = 1010; 7 8 #define INF 1e9; 9 10 int t, N, X, Y, MAX; 11 int X1[MAXLEN] = { 0 }, X2[MAXLEN] = { 0 }, H[MAXLEN] = { 0 }, LeftMinTime[MAXLEN] = { 0 }, RightMinTime[MAXLEN] = { 0 }; 12 13 void h_sort(int X1[], int X2[], int H[]) { 14 for (int i = 0; i < N; i++) { 15 for (int j = i + 1; j < N; j++) { 16 if (H[j] > H[i]) { 17 int temp; 18 temp = H[i]; 19 H[i] = H[j]; 20 H[j] = temp; 21 temp = X1[i]; 22 X1[i] = X1[j]; 23 X1[j] = temp; 24 temp = X2[i]; 25 X2[i] = X2[j]; 26 X2[j] = temp; 27 } 28 } 29 } 30 } 31 32 int find(int x, int h) { 33 for (int i = 0; i < N; i++) { 34 if (x >= X1[i] && x <= X2[i]) { 35 if (h > H[i] && H[i] != 0) 36 return i; 37 } 38 } 39 return -1; 40 } 41 42 int main() { 43 cin >> t; 44 while (t--) { 45 memset(X1, 0, sizeof(X1)); 46 memset(X2, 0, sizeof(X2)); 47 memset(H, 0, sizeof(H)); 48 memset(LeftMinTime, 0, sizeof(LeftMinTime)); 49 memset(RightMinTime, 0, sizeof(RightMinTime)); 50 cin >> N >> X >> Y >> MAX; 51 for (int i = 0; i < N; i++) 52 cin >> X1[i] >> X2[i] >> H[i]; 53 54 //排序 55 h_sort(X1, X2, H); 56 //第一块板子 57 int key = find(X, Y); 58 59 if (key == -1) { 60 cout << Y << endl; 61 continue; 62 } 63 64 for (int i = N - 1; i >= 0; i--) { 65 int m = find(X1[i], H[i]); 66 if (m == -1) { 67 if (H[i] > MAX) { 68 LeftMinTime[i] = INF; 69 } 70 else { 71 LeftMinTime[i] = H[i]; 72 } 73 } 74 else { 75 if(H[i] - H[m] <= MAX) 76 LeftMinTime[i] = H[i] - H[m] + min(LeftMinTime[m] + X1[i] - X1[m], RightMinTime[m] + X2[m] - X1[i]); 77 else 78 LeftMinTime[i] = INF; 79 } 80 int r = find(X2[i], H[i]); 81 if (r == -1) { 82 if (H[i] > MAX) { 83 RightMinTime[i] = INF; 84 } 85 else { 86 RightMinTime[i] = H[i]; 87 } 88 } 89 else { 90 if(H[i] - H[r] <= MAX) 91 RightMinTime[i] = H[i] - H[r] + min(LeftMinTime[r] + X2[i] - X1[r], RightMinTime[r] + X2[r] - X2[i]); 92 else 93 RightMinTime[i] = INF; 94 } 95 } 96 int minTime = Y - H[key] + min(LeftMinTime[key] + X - X1[key], RightMinTime[key] + X2[key] - X); 97 cout << minTime << endl;; 98 } 99 return 0; 100 }