耿直：统计学中的因果推断问题（Causal Inference）

来源：量化研究方法

本文约3000字，建议阅读5分钟。

数学科学学院耿直老师为你介绍统计学中的因果推断问题。

今天，小编带来了数学科学学院耿直老师关于统计学中因果推断问题的介绍。文中介绍了几种分析因果关系的主要模型，并进一步介绍了混杂因素与工具变量、中间因素问题、多因素间的因果关系问题等统计学中的挑战性课题，最后指出，在人类的计算能力大幅度提高的今天，缺乏从数据中认知因果关系的方法，仍然是对人类求知之路的最大阻碍；对这一问题的研究将为各领域知识疆界的拓广提供重要的贡献。

因果推断

（Causal Inference）

耿直

北京大学数学科学学院

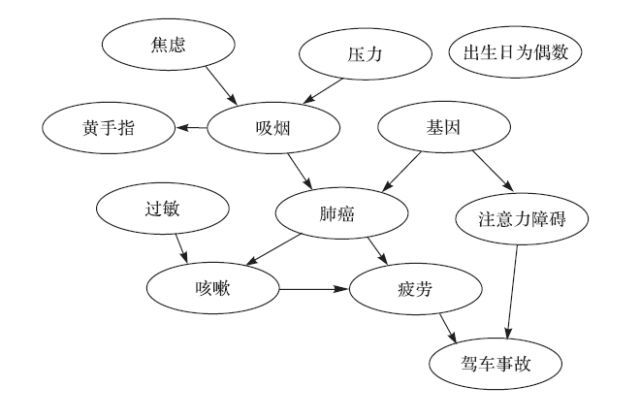
一个现象的出现总是伴随着另一个现象的出现，改变其中之一是否会导致另一个跟着变化？其答案取决于这两个现象之间仅有相关关系？还是有因果关系？自古以来，关于因果关系的研究一直吸引着人们去思考。在科学研究中，人们通过观察和实验发现自然规律、探索现象之间的因果关系是各种科学研究的最终目标。爱因斯坦认为“西方科学是建立在以因果律为基础的形式逻辑之上”。自1888年Galton提出了相关系数的概念以来，“涉及因果推断的问题自始就缠住了统计学的脚后跟”[1]，1911年，Pearson提出用列联表分析因果关系，1921年，Wright提出路径分析模型，1934年，Neyman提出潜在结果模型，1935年，Fisher提出随机化试验方法，1974年，Rubin关于观察性研究提出虚拟事实模型，Pearl[2]和Spirtes等[3]提出因果网络图模型，图1给出了一个设想的关于肺癌的因果网络[4]。Freedman介绍了从相关关系研究到因果关系研究的发展过程。从观察获得的数据中发现，不同因素之间的因果关系是统计学和人工智能领域长期关注的科学难题。

图为关于肺癌的因果网络

Yule-Simpson悖论描述了一种与人们常识相悖的现象，一种药品对男性和女性都有效，但对人类无效。无因果关系的两个因素A和B可能会有相关关系，这个相关关系是由于其他因素C对它们共同影响所造成的，因素C称为混杂因素。混杂因素也可能会使原本有因果关系的两个因素变得互不相关。例如，设想有一种治疗某种病危患者的特效药，而且所有患者都服用了这种药，那么，会观察到服药的患者与不服药的正常人有相同的寿命，即服药与寿命不相关。判断是否存在混杂因素是因果推断的关键问题[6]。采用随机化试验，即给每个患者随机地分配治疗或处理方案，可以排除混杂因素。随机化试验是因果推断的最可靠方法，但随机化试验需事先确定哪个因素是原因，其目的是推断原因对结果的作用，而且在很多研究中不允许进行随机化试验。但是，根据观察性研究进行因果推断需要某种用数据不可证伪的假定[1]。通常，假定观察了足够多的变量，以致包含了所有的混杂因素。在观察性研究中，首先确定观测变量的集合，然后从中选择混杂因素是因果推断的两个关键步骤。当存在未知的或不可观测的混杂因素时，可以选择一个与原因变量相关，但不受混杂因素影响的变量称为工具变量，来消除混杂偏倚，而根据先验知识很难确保不受混杂因素影响。因此，确定和选择工具变量是另一个具有挑战性的研究课题。

图为提出随机化试验方法的英国统计学家Ronald Fisher（1890-1962）

在科学研究中，常探究原因影响结果的因果机制，原因A对结果B的直接作用有多大，而原因A通过中间因素C对结果B的间接作用有多大。给定中间因素C取相同值的条件下，根据A对B的作用来评价直接作用的方法可能会导致错误的结论。例如，给定接受新治疗与接受对照治疗的患者的中间因素血压C取相同值的病人并不是同一类病人，不具有可比性。为了保证可比性，Frangakis和Robin提出主分层方法，根据每个人的潜在中间因素（接受新治疗的血压和接受对照治疗的血压）将总体分层。但是，同一个人只接受一种治疗，因此，只能观测到一个血压，而不能两者兼得，导致主分层方法遇到了新的困难。

在科学研究中，人们常试图利用一个近期的或容易得到的中间指标来替代远期的或难以得到的终点指标。确定替代指标方法有基于条件独立性、主分层和因果图的准则。但是，采用这些准则可能会出现因素A对因素B有正作用，并且因素B对因素C也有正作用，而出现因素A对因素C 有负作用的现象，称为替代指标悖论或中间因素悖论[7]。近年来，很多专家对替代指标方法进行了争议。抑制心律失常能降低发生心脏骤停的可能性，曾将抑制心律失常作为评价治疗猝死药物的替代指标。美国批准了几种能有效抑制心律失常的药品，但是，经过长期追踪研究发现，这些药品不但没有降低心脏骤停的可能性，发而增加了可能性，这就是美国20世纪80年代发生的历史上最严重的药品灾难事件。在科学研究中，采用将一个复杂系统分解为各部分之组合的还原论方法和采用替代指标的方法的合理性都有待于从因果推断的角度进行审视。

图为美国统计学家Donald Robin，Robin教授，

将于今年9月全职赴清华大学丘成桐数学中心工作

基于相关关系的预测仅适用于学习样本和未来样本是同分布的情况。外部干预可能会改变变量之间的相关性和总体的分布。基于因果机制的预测方法建立因果模型，对未来外部干预的结果进行预测。基于因果关系的方法可以预测制止公鸡打鸣不会阻挡日出，因此，它比基于相关关系的预测方法更具有普适性。对于历史数据中未曾经验过的干预进行预测是一个具有挑战性的问题[4,8]。

目前，多因素之间因果关系研究主要采用Bayes网络模型。因果Bayes网络已经被广泛应用于多学科的研究中。在生物信息学研究中，使用小样本数据构建数千个基因的调控网络，这种高维小样本数据的网络结构学习同时具有计算复杂性和统计效率的问题。基于Bayes网络的因果推断注重从数据中挖掘因果关系，而仅仅从观察数据是否能发现因果关系的问题仍存在争论。根据观察数据和试验数据学习构建因果网络是一个具有挑战性的研究问题[2-4,9]。

一百年前发现了相关关系的数学描述，推动了人类对自然科学和人文社会奥秘的认知能力。20世纪计算机的出现使得人们的计算能力得到了飞跃，大大增强了数据分析的能力。当今，计算机网络和生物芯片等技术的出现，使得人们获得数据的手段更加丰富。尽管从数据中挖掘相关关系的方法研究发展迅速，但分析挖掘因果关系的方法还非常贫乏。“在过去的一个世纪中，许多发现被推迟是由于缺少描述因果的数学语言。”[2] 目前，在科学研究中妨碍人们认知自然科学和人文社会奥秘的一个最大障碍也许是缺乏从数据中认知因果关系的方法。人们在认知因果方法上的进步将提升人类更深层次地认知自然科学和人文社会奥秘的能力。因果推断领域向统计学、机器学习和人工智能提出了各种具有挑战性的重要研究问题，其中包括基于观察数据评价因果作用的方法，探究直接作用和间接作用等因果机制的方法，基于因果模型对外部干预进行预测的方法，从高维数据、混合类型数据、多源数据、时间序列数据、不完全数据及含隐变量等复杂数据中挖掘因果关系和因果网络的方法等。

注释：

[1] Holland P W. Statistics and causal inference. J. Am. Statist. Ass. , 1986, 81:945-970.

[2] Pearl J. Causality: Models, Reasoning, and Inference. 2nd ed. Cambridge: Cambridge University Press, 2009.

[3] Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search. 2nd ed. New York: MIT Press, 2000.

[4] Guyon I, Aliferis C, Cooper G, et al. Causation and prediction challenge. Proceed. J. Mach. Learn, Res. 2008, 3.

[5] Freedman D. From association to causation: Some remarks on the history of statistics, Statistical Science, 1999, 14:243-258.

[6] Greenland S, Robins J M, Pearl J. Confounding, and collapsibility in

causal inference. Statistical Science, 1999, 14:29-46.

[7] Ju C, Geng Z, Criteria for surrogate endpoints based on causal distributions, J. Royal Statist. Soc. B, 2010, 72:129-142.

[8] Heckman J J. Econometric causality. Internat. Statist. Review, 2008, 76:1-27.

[9] http://jmlr.csail.mit.edu/papers/topic/causality.html.

本文转载自公众号量化研究方法，来源：通识联播，作者：耿直，本文原载于《10000个科学难题信息科学卷》，北京：科学出版社，2011，第647-650页。

编辑：文婧