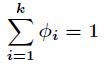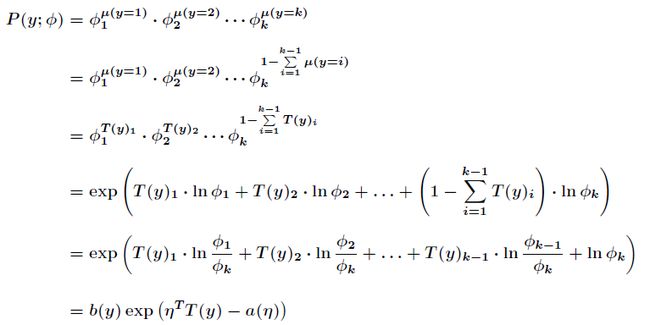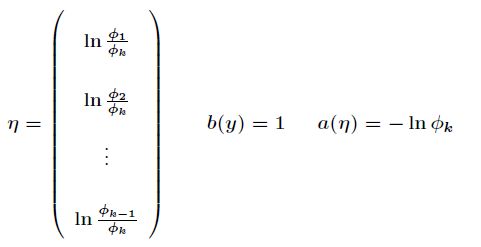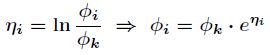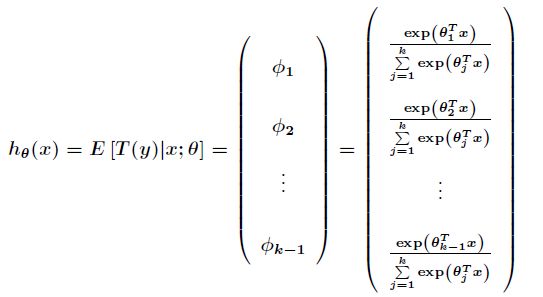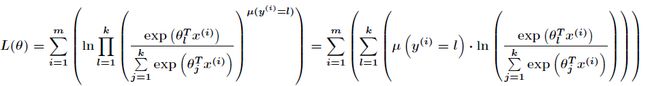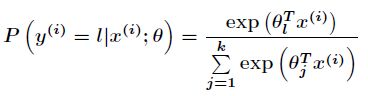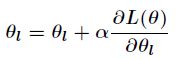softmax回归
转自:http://blog.csdn.net/acdreamers/article/details/44663305
在上一篇文章中,讲述了广义线性模型。通过详细的讲解,针对某类指数分布族建立对应的广义线性模型。在本篇文章
中,将继续来探讨广义线性模型的一个重要例子,它可以看成是Logistic回归的扩展,即softmax回归。
我们知道Logistic回归只能进行二分类,因为它的随机变量的取值只能是0或者1,那么如果我们面对多分类问题怎么
办?比如要将一封新收到的邮件分为垃圾邮件,个人邮件,还是工作邮件;根据病人的病情预测病人属于哪种病;对于
诸如MNIST手写数字分类(MNIST是一个手写数字识别库,相见:http://yann.lecun.com/exdb/mnist/)。诸
如此类问题都涉及到多分类,那么今天要讲的softmax回归能解决这类问题。
在Logistic回归中,样本数据的值![]() ,而在softmax回归中
,而在softmax回归中![]() ,其中
,其中![]() 是类别种数,
是类别种数,
比如在手写识别中![]() ,表示要识别的10个数字。设
,表示要识别的10个数字。设
![]()
那么
而且有
为了将多项式模型表述成指数分布族,先引入![]() ,它是一个
,它是一个![]() 维的向量,那么
维的向量,那么
应用于一般线性模型,![]() 必然是属于
必然是属于![]() 个类中的一种。用
个类中的一种。用![]() 表示
表示![]() 为真,同样当
为真,同样当![]() 为假时,有
为假时,有
![]() ,那么进一步得到联合分布的概率密度函数为
,那么进一步得到联合分布的概率密度函数为
对比一下,可以得到
由于
那么最终得到
可以得到期望值为
接下来得到对数似然函数函数为
其中![]() 是一个
是一个![]() 的矩阵,代表这
的矩阵,代表这![]() 个类的所有训练参数,每个类的参数是一个
个类的所有训练参数,每个类的参数是一个![]() 维的向量。所以在
维的向量。所以在
softmax回归中将![]() 分类为类别
分类为类别![]() 的概率为
的概率为
跟Logistic回归一样,softmax也可以用梯度下降法或者牛顿迭代法求解,对对数似然函数求偏导数,得到
然后我们可以通过梯度上升法来更新参数
注意这里![]() 是第
是第![]() 个类的所有参数,它是一个向量。
个类的所有参数,它是一个向量。
在softmax回归中直接用上述对数似然函数是不能更新参数的,因为它存在冗余的参数,通常用牛顿方法中的Hessian
矩阵也不可逆,是一个非凸函数,那么可以通过添加一个权重衰减项来修改代价函数,使得代价函数是凸函数,并且
得到的Hessian矩阵可逆。更多详情参考如下链接。
链接:http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
这里面也讲述了K个二元分类器与softmax的区别,值得学习。
参考资料:
(1)http://www.cnblogs.com/tornadomeet/archive/2013/03/22/2975978.html
(2)http://www.cnblogs.com/tornadomeet/archive/2013/03/23/2977621.html
(3)http://demo.netfoucs.com/lingerlanlan/article/details/38410123
(4)http://freemind.pluskid.org/machine-learning/softmax-vs-softmax-loss-numerical-stability/
(5)http://blog.csdn.net/celerychen2009/article/details/9014797