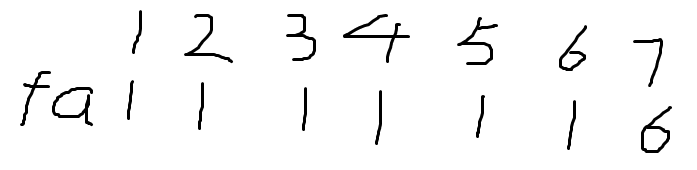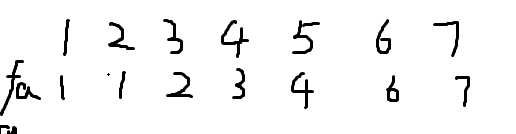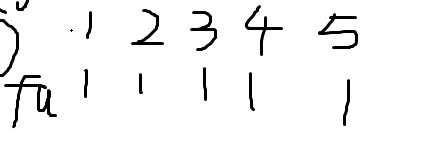POJ 1703 Find them, Catch them // 种类并查集 自己的详细理解过程 回溯过程
Description
Assume N (N <= 10^5) criminals are currently in Tadu City, numbered from 1 to N. And of course, at least one of them belongs to Gang Dragon, and the same for Gang Snake. You will be given M (M <= 10^5) messages in sequence, which are in the following two kinds:
1. D [a] [b]
where [a] and [b] are the numbers of two criminals, and they belong to different gangs.
2. A [a] [b]
where [a] and [b] are the numbers of two criminals. This requires you to decide whether a and b belong to a same gang.
Input
Output
Sample Input
1 5 5 A 1 2 D 1 2 A 1 2 D 2 4 A 1 4
Sample Output
Not sure yet. In different gangs. In the same gang.
Source
明确一下规则,0代表两者是通过关系,1代表两者不是同伙关系。
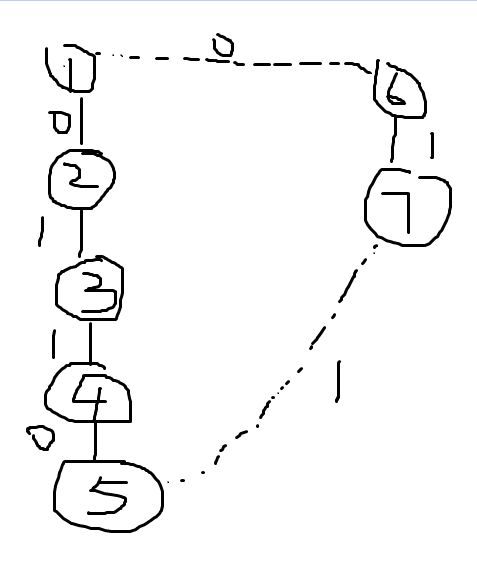
首先先举一个例子,举的例子完全按照我个人意愿,与题目给的例子没有关系,假如有两个集合,一个集合里面有数字1 2 3 4 5,另一个集合里面的数字有6 7,我现在输入D 6 7,代表6和7之间是在不同的团伙的,那么通过这个例子,来讲解算法思路。
用数组代表下面的关系集合 fa数组中存放的是根节点,gang数组中存放的是节点与根节点的关系(0或者1)
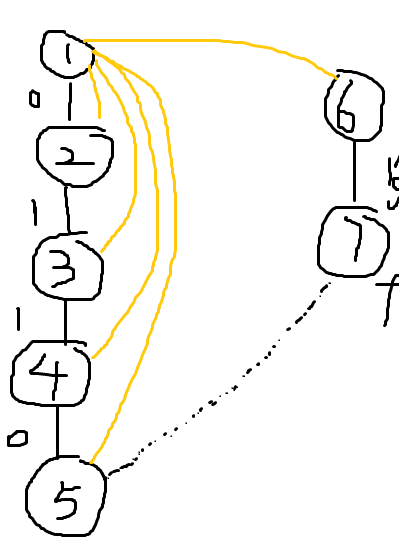
5和7之间建立了关系,关系是1,那么关系的过程是怎么建立的呢!
输入D 5 7 之后进入函数union_set(5,7)中,在union_set(5,7),
void union_set(int a,int b)
{
int roota=Find(a);
int rootb=Find(b);
if(roota!=rootb)
{
fa[rootb]=roota;
gang[rootb]=(gang[a]+gang[b]+1)%2;
}
}这个函数里,又调用了Find()函数,Find函数是用来找根的函数,我们从5开始找。
I.Find(5):
int Find(int x)
{
if(fa[x]==x)
return x;
int temp=fa[x];
fa[x]=Find(temp);
gang[x]=(gang[x]+gang[temp])%2;
return fa[x];
}详细的执行过程如下:(返回后的语句是 回溯过程)
1.x=5,不满足if语句,执行下面的语句。
2.x=5,temp =fa[5] =4,递归调用Find()函数, fa[5]=Find(4); 返回后:x=5,fa[5]=1(这个1是上层返回的1),temp=4,
gang[x]=(gang[x]+gang[temp])%2; 更新的是 5和4的关系3. x=4,temp =fa[4]=3,递归调用Find()函数,fa[4]=Find(3); 返回后:x=4,fa[4]=1(这个1是上层返回的1),temp=3,
gang[x]=(gang[x]+gang[temp])%2; 更新的是 4和3的关系4.x=3,temp=fa[3]=2,递归调用Find()函数,fa[3]=Find(2); 返回后:x=3,fa[3]=1(这个1是上层返回的1),temp=2,
gang[x]=(gang[x]+gang[temp])%2; 更新3和2的关系。5.x=2,temp=fa[2]=1,递归调用Find()函数,fa[2]=Find(1); 返回后:x=2,fa[2]=1(这个1是上层返回的1),temp=1,
gang[x]=(gang[x]+gang[temp])%2; 更新的是2和1的关系,
执行完这一句后,又return fa[x],(此时x是等于2的,fa[2]=1),返回的是 1 。
6.因为fa[1]==1,所以执行return x语句,返回上一层
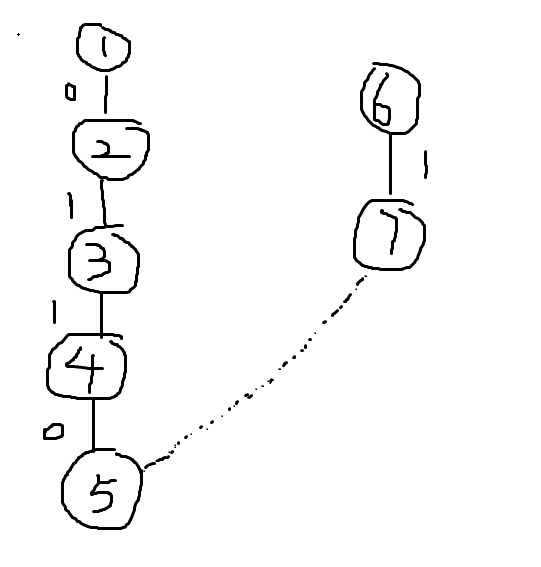
通过这个执行过程改变的是节点的父节点(将所有节点的父节点,均改为了这个集合总关系的总根节点)。由上图的关系,变成了下图的关系
IIFind(7):
1.x=7,不满足if语句,执行下面的语句。
2.x=7,temp =fa[7] =6,递归调用Find()函数, fa[7]=Find(6); 返回后:x=7,fa[7]=6(这个1是上层返回的6),temp=6,
gang[x]=(gang[x]+gang[temp])%2; 更新的是 7和6的关系3.因为fa[6]==6,所以执行return x语句,返回上一层
这样所有节点就和其总的根节点建立好了,然后就去执行
if(roota!=rootb)
{
fa[rootb]=roota;
gang[rootb]=(gang[a]+gang[b]+1)%2;
这个判断语句,这样一句的判断目的在于看5和7这两个节点是否在同一个集团里,如果在同一个集团里,那么就不用在fa[]数组中建立联系,当输入A 5 7 时就可以直接判断出5和7是0还是1的关系;如果不在同一个集团里,那么就要将5和7的总根节点进行连接,它们的总根建立关系了,就好判断总根下的各个节点的关系了。
gang[rootb]=(gang[a]+gang[b]+1)%2; 通过建立两节点总根的关系,来确定两节点 5 和7 的关系,说白了就是将两集团连接起来