CT系统参数标定及成像

摘要
CT可以在不破坏样品的情况下，利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像，由此获取样品内部的结构信息。但由于CT系统安装时往往存在误差，影响成像质量。因此利用数学知识，借助于已知结构的样品（称为模板）标定CT系统的参数，解决相关问题。
首先，由本文图示可知该CT为单束旋转平移CT，了解学习其运动轨迹，对已知数据进行分析和预处理，了解数据和图例模型的关系，分析其形状和旋转方式，根据其运动规律和形状特征分析其旋转中心点，细心观察经预处理的数据发现X射线与圆的关系求得X射线间的间隔距离，和经大量查阅资料以及预处理数据后的数据特征得出180次运动方向。
然后，根据上述已求得的信息可以建立成像模型用已知的模版进行验证对比进行调整测试，用调试好的标定模型——反投影法模型，进行数据可视化将本题给的扫描接受数据进行成像，得到数据形状等信息。
其次，通过建立坐标系以及坐标系的多次转换和单位的转换，使扫描CT与模版托盘一体化，达到坐标转换以及相对位置转换，从而能清楚精确的定位托盘模版在扫描仪的位置，扫描仪在托盘模版的相对位置。进而精准明确的表达出如题所示的十个点的吸收率。
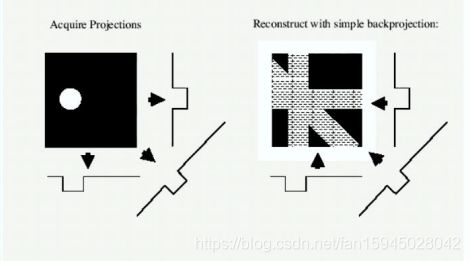
最后，通过对以上问题和数据以及成像图片的分析，觉的存在误差，成像模糊出现星形伪迹，从而最效果有很大的影响，本文通过滤波(卷积)反投影法对模糊图形进行滤波去噪使星形伪迹减弱甚至消失，然后对以上问题进行重新图像重建得到清晰的图形和结果，亦可以自己造模版进行检验，本文通过matlab自建模版进行模型验证分析，亦可得出清晰成像结果。

关键字： 反投影法 滤波(卷积)反投影法 图像去噪 数据可视化

一、问题重述
CT是一种融合了射线光电子学、微电子学等学科的技术，因其可无损检测而被广泛应用到医学，工业，生物，航天等多个领域。当X光照射物体时，物体的各个部分对X光的吸收和折射率不同，因而X光的衰减程度有所差异。重建法正是利用这个现象，使接收器接收到不同强度的X射线，再由一系列转换求出灰度分布情况，进而得到断层图像。
CT技术发展初期，CT只能使用单一探测器进行平移扫描加旋转扫描，也就是题中的二维CT系统。随着X射线源以及探测器单元在同一方向的同步位移，可以得到同一视角下的一组投影数据。CT系统通过不停围绕某一旋转中心进行旋转，重复平行束扫描，对每一个X射线方向，在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后接收到180组投影数据。多次进行CT扫描获得被测物体在这些视角下的多组投影数据，最后可以用于图像重建。
但是由于CT安装过程中容易产生误差，经常导致重建图像产生伪影，极大地阻碍了后续利用图像进行尺度测量、密度测量、面积测量等工作。为了解决由误差引起的一系列问题，本文对安装好的CT系统进行标定，并解决下列问题。
1.问题一要求我们通过建立模型，利用已知模板的几何信息、吸收率以及接受情况，求解CT系统旋转所围绕的旋转中心在托盘上的位置、等距单元探测器上各单元之间的距离以及该CT系逆时针旋转时X射线的180个方向，确定标定参数。
2.问题二、三：两个问题的大体思路一致，皆是通过利用问题一得出的标定参数，反推确定某一未知介质在正方形托盘中的位置、几何形状和吸收率等相关信息。同时，确定出所给10个位置处的吸收率。
3.问题四：利用（1）中所得的标定参数的精确度以及CT系统的稳定性，以此为基础，自行改进，设计新的模板并建立新的对应模型，并说明使用这种改进方法的原因。

二、问题分析
CT系统安装过程容易出现误差，从而引起成像质量问题。在这种情况下，为了减少误差，要对CT系统进行软件分析，故而对安装好的CT系统进行参数标定。就是要建立一种模型，解决计算介质位置，形状，大小及是否均匀等情况并成像，从而达到目的。

问题一分析：
512束通过单束平移的运动方式旋转180次测得数据，可以求得分别穿过介质和空白位置的X光数。用matlab将射线分为衰减射线和未衰减射线。发现通过小的X光数量几乎不变，由此计算出像素。通过求正方形四个边的位置，确定其中心即为旋转中心。接着判断180扫描的方向。

问题二、三分析
在某一断面，各点的密度值可以看成穿过该平面内该点的射线的投影值的均值，据（1）所得的标定参数，根据两种未知介质的接收情况，利用反投影重建法求出该点的密度，将每一次扫描的数据转化成矩阵进行叠加，结果即为成像图形的灰度像素矩阵。进而成像求解该介质的在正方形托盘中位置，几何形状及吸收率等相关信息，并确定图3中10个点的吸收率。

问题四分析：
但是在计算过程中我们可以发现，由于角度的不同，这种叠加过程会使我们在原本没有介质存在的点计算出均值，影响准确度，形成重影，影响各个因素的判断。这种情况称之为星状伪迹。为了修正，我们在问题四中引入卷积反投影法，使所得数据与卷积因子相乘，通过计算，使投影数据值中正负数值相互抵消，根据系统显示的不同矩阵的大小，各投影滤过的原始数据被投影成像并显示出去掉晕伪影的清晰真实图像。

三、模型假设
1.附件中所提供的数据都是可靠有效，能反应真实情况的；
2.正方形托盘和整个发射-接收系统在旋转的过程中，各自所处的平面保持不变，且二者所处的平面平行；
3.忽略光的其他波动现象，假设光只以直线传播；
4.忽略X辐射光源的大小和形状，作为质点考虑。

四、符号说明
符号 说明
d X射线间隔（mm）
小球挡住X射线条数
D 小球直径
L1 X射线转到垂直椭圆长轴左侧边缘点距模板边缘像素
L2 X射线转到垂直椭圆长轴右侧边缘点距模板边缘像素
L3 X射线转到平行椭圆长轴左侧边缘点距模板边缘像素
L4 X射线转到平行椭圆长轴右侧边缘点距模板边缘像素
n1 X射线转到垂直椭圆长轴左侧未衰减X射线条数
n2 X射线转到垂直椭圆长轴中间衰减X射线条数
n3 X射线转到垂直椭圆长轴右侧未衰减X射线条数
x1 ：X射线转到平行椭圆长轴左边未衰减X射线条数
x2 X射线转到平行椭圆长轴通过园衰减X射线条数
x3 X射线转到平行椭圆长轴椭圆与圆之间未衰减X射线条数
x4 X射线转到平行椭圆长轴通过椭圆衰减X射线条数
x5 X射线转到平行椭圆长轴右侧未衰减X射线条数
I0 起始X射线强度
dX X射线通过待测物体的厚度
-dI 强度衰减量
M 衰减系数
α 起始旋转时平行的X射线发出器和接收器与模板偏转角
Z 投影值
p 像素（投影值均值）

五、模型的建立与求解
5.1问题一
5.1.1模型建立与求解
1963年，科马克美国物理学家发现人的不同组织对X射线的透过率不同，经研究发现得出一系列计算公式，正是因为这些计算公式奠定了CT在医学界物理学界的基础。由于X射线透过待测材料衰减的特性接收器会得到不尽相同的值，正是这些数据中隐藏的信息给了我们还原他们的可能。CT种类繁多例如单束平移旋转CT、窄扇形束平移旋转CT、静止旋转CT、螺旋扫描CT等等不胜枚举。本题研究的CT为单束平移旋转CT但是未涉及到平移。
本题第一小问X射线间隔问题：利用matlab进行分类将X射线分有衰减射线和无衰减射线,无衰减射线接受数据为0，有衰减射线接受数据不为0，以是否为0作为依据对接受信息附件sheet2进行查找，具体matlab程序见附录程序一，当X射线与椭圆长轴垂直时射线分类情况及每类的条数如图一所示

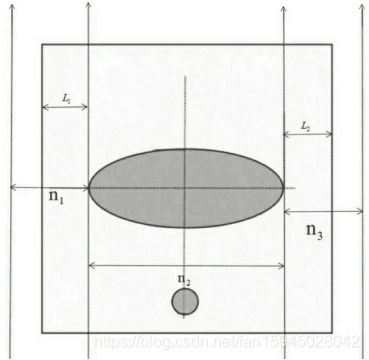
图 1

当X射线与椭圆长轴平行时射线分类情况及每类的条数如图二所示

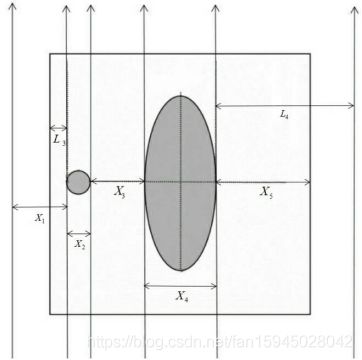
图 2

由分类数据可轻易看出有一个值大体是恒定不变的因为该数据表示X射线通过圆的衰减射线条数如表一所示

表 1
由于再次我们取平均值条X射线有衰减现象可得d为0.2909毫米如下：

5.1.2模型建立与求解
本论文通过求正方形的四条边从而确定正方形的中心。如图1所示最下侧的X射线为CT的射线的最下边缘，最上侧的X射线为为CT的射线的最上侧边缘。如图2所示最左侧的X射线为CT的射线的最左边缘，最右侧的X射线为为CT的射线的最右侧边缘。有上图的4个边缘组成一个正方形，该正方形中心为CT扫描的旋转中心O1，并且可求O在模版中的以模版坐下角为原点O2的坐标，本论文采用填补法，将X射线4个边缘组成的正方形填补到原来模版周围，用如下公式求模版各个边需要填补的像素：

运用matlab进行像素填补填补结果为一个大的正方形包含着模版matlab程序见附录程序二填补结果如图三：

图 3

接着求出大正方形的中心的像素坐标，大正方形的像素矩阵r为370*372，由于误差不到1mm，所以本题忽略不记，旋转中心为正方形像素中性r(185,186),将像素中心转化为以模版左下角O2为原点的坐标(m,n)，转换公式如下：

O1为旋转中心其在模版上的位置如上图白色标记，坐标为：

5.1.3模型建立与求解
由于本CT为单束平移旋转CT由多方查阅资料得知本CT扫描一个待测物体需要旋转180度每次转1度才可成像根据程序一得出X射线分类条数分析，最大时CT位置和托盘相对位置为X射线垂直椭圆长轴如图一所示此时看程序一数据可知CT旋转第61次，当最大时CT位置和托盘相对位置为X射线平行椭圆长轴如图二所示此时看程序一数 据可知CT旋转第151次。由如上信息可得出结论该CT初始旋转位置与模版相对位置如图四所示。

图 4

5.2问题二、三
5.2.1模型建立与求解
1.基本思想：断层平面成像是有灰度像素点的值大小进行的，也可以说是投影值大小决定的，该平面中某一点的密度函数值可以看作全部经过这一点的X射线的投影值的平均值。然后投影值的平均值即可当作灰度像素进行成像。
图例解释：
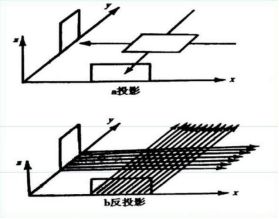
因为该CT旋转180次每次1度所以没扫描一次可其余次数得到的投影值联立起来就会构成图形信息，从而达到了图形重构的目的，成像原理如下：

图 5

图 6

2.举例说明：如图所示（n）为第n个X射线求出每条射线投影值，然后求出叠加后的灰度像素（叠加投影值均值）

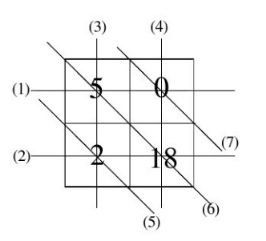
图 7

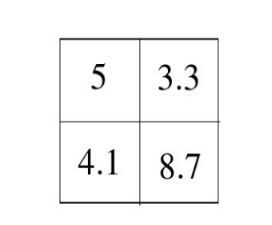
图 8

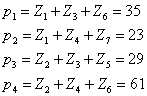
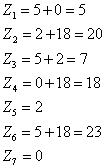
求平均（除以射线条数）：


3.算法说明：本文用matlab进行算法实现，由于所给数据一列为一次扫描一列512个数180列，将题中所给的512180接受的数据进行拆分，将一列作为一个投影层。首先，将一列进行复制将第i列变成一个512512的矩阵，该矩阵没一列都是由第i列复制来的，由此可以得到180个矩阵，将第i+1个矩阵旋转1度加到第i个矩阵上，知道加完180个，然后除以射线条数，得到的512512的矩阵为所要成像图形的灰度像素矩阵，然后进行等比例缩小成体重要求的256256大小可得。程序见附录程序三，第一问结果如图九，第二问结果如图十，第三问结果如图十一.

图 9

图 10

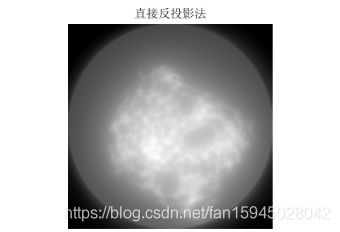
图 11

5.2.2模型建立与求解
由上图可以很容易的看出待测成像物体的几何特征和待测物体在托盘中的位置如第二问举例显示其在托盘中的位置黑色正方形框为托盘以及本题可给出十个固定点的吸收率信息由本体附件可得到该十个点的准确坐标，建立模型实现成像与托盘的坐标互换，模型如下图十二，及托盘上以托盘坐下角O2为原点的坐标系上的十个点的坐标为本题附件sheet4所给数据，将这些坐标转换成以CT旋转中心O1为原点的坐标系坐标：

(单位：毫米)
然后将以CT旋转中心O1为原点的坐标系坐标转换成将该坐标轴顺时针旋转度的坐标轴坐标：

(单位：毫米)
将单位为毫米的坐标转变成以像素为单位的坐标，因为成像灰度像素矩阵为256*256，由于该CT有512个X射线511个间隔所以该成像图像实际是以M长为边的正方形，一毫米可代表j个像素：



(单位：像素)
再次转换坐标将，此时坐标系是以CT旋转中心点（灰度像素矩阵中心）建立的，将之转换成以灰度像素矩阵左下角O3为原点建立的坐标：
(单位：像素)

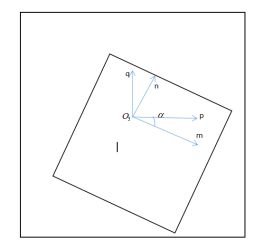
图 12

根据上述模型可求的本题所求的十个点坐标在灰度像素矩阵中的相应像素坐标可得吸收率，程序见附录程序六，第二问图形在托盘中位置示意图如下图13，第一行为第二问十个点，第二行为第三问十个点，十个点在二三问中的具体吸收率如下表：

图 13

表 2

5.3问题四
5.3.1模型建立与求解
滤波处理模型：如上星状轨迹分析以说明误差和模糊产生原因本模型的目的就是为了将灰度像素矩阵中原本为0和不应该变化的使之变化了，出现边缘失锐效应，需要用对原来的灰度像素矩阵进行有效的滤波，使用滤波函数与灰度像素信号做叠

加运算处理，让灰度像素值再它两旁出现正和负成分，形成所谓的滤波灰度像素值，经过多次数值迭加，可让正和负几乎相互抵消，从而失锐效应消除，最后成像与原像更接近，这种滤波等效于将灰度像素矩阵第i列和进行卷积的到新的滤波矩阵第i列为。

滤波函数为第i列数据个数*2-1长度的一列数据，需要对该列进行设置数值以达到滤波的作用，首先都赋值为0，i为1到512，然后在进行详细设置如下：

{ （i为偶数）
{（i为奇数）

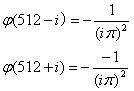
由滤波公式与原来灰度像素矩阵每一列进行卷积，得到了消除边缘失锐的灰度像素矩阵再用原本未滤波的模型进行图形重建运算，程序见附录程序四，结果以及效果如下：

图 14

图 15

图 16

5.3.2模型建立与求解
误差以及原因已经分析完，下面自行建立一个模版对本模型进行检验和阐述，利用matlab函数自动获取一个头骨图形仿体，对仿体的灰度像素矩阵进行拆分，拆分成本题附件所给CT扫瞄的接受数据形式，然后再行图形重建，先利用原来未滤波的模型再进行滤波模型重建，程序见附录程序五，结果如下图：

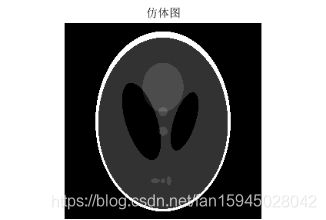
图 17

图 18

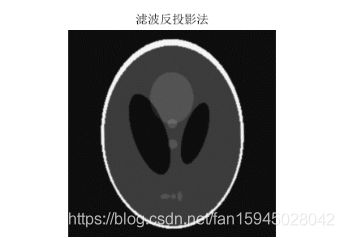
图 19

六、模型的讨论与推广

一、误差分析：
1.模型在理想情况下建立，模型中载物台与地面绝对平行。在实际使用中，载物台可能2.与地面有一定角度，影响投影。
3.X光发生器可能与载物台有一定俯仰角，会使投影有一定偏差。
4.像素不够大引起的误差。
5.题中数据不够精确而引起的误差。

二、模型评价与推广：
反投影重建算法利用变换重建公式，能直接成像，速度较快，易于实现，对基函数的要求并不是很苛刻，但密度为0的点叠加后发生变化，即使修正也会引起成像的变化。而卷积反投影法对前期成像修正效果明显，使成像更清晰准确。该模型可用于工业，医学，生物，航天等多个领悟，为完成清晰准确的成像提供了较好的模型。

七、参考文献
[1]向前. 锥束CT几何参数校正方法研究[D].重庆大学,2016.
[2]吴梦秋,程正兴. 反投影重建算法的改进算法[J]. 西安工业学院学报,2004,(01):76-81. [2017-09-17]. DOI：10.16185/j.jxatu.edu.cn.2004.01.019
[3]王志伟,于强,舒春梅,谭润初,贺奇才. 计算机模拟CT滤波反投影重建的方法[J]. 中国医学物理学杂志,2010,27(02):1737-1740. [2017-09-17].
[4]范慧赟. CT图像滤波反投影重建算法的研究[D].西北工业大学,2007.
[5]韦钰,柴振明. 卷积—反投影CT图象重组法的模拟研究[J]. 南京工学院学报,1983,(02):41-48. [2017-09-17].
[6]齐宏亮. 稀疏角度下的CT图像重建迭代算法研究[D].南方医科大学,2013.第6页

八、附录
程序一
load(‘DATA2’)
[x,y]=size(DATA2);
n1=0;
n2=0;
n3=0;
n4=0;
n5=0;
s=ones(180,5);
for j=1:y
for i=1:x
if(DATA2(i,j)==0)
n1=n1+1;
end
if(DATA2(i,j)>0)
break;
end
end
for i=n1+1:x
if(DATA2(i,j)>0)
n2=n2+1;
end
if(DATA2(i,j)==0)
break;
end
end
for i=n1+n2+1:x
if(DATA2(i,j)==0)
n3=n3+1;
end
if(DATA2(i,j)>0)
break;
end
end
for i=n1+n2+n3+1:x
if(DATA2(i,j)>0)
n4=n4+1;
end
if(DATA2(i,j)==0)
break;
end
end
for i=n1+n2+n3+n4+1:x
if(DATA2(i,j)==0)
n5=n5+1;
end
end
N=[n1,n2,n3,n4,n5];
s(j,:)=N;%宽度矩阵
n1=0;
n2=0;
n3=0;
n4=0;
n5=0;
end

程序二
load(‘DATA1’)
o1=zeros(74,256);
o2=zeros(330,84);
o3=zeros(330,32);
o4=zeros(40,372);
q=[o1;~DATA1];
w=[o2,q];
e=[w,o3];
r=[e;o4];
imshow®;
m=round(370/2);
n=round(372/2);
for i=1:2:8
r(m-i,n-i)=1;
r(m+i,n+i)=1;
r(m+i,n-i)=1;
r(m-i,n+i)=1;
end
zhongxin=r(m,n);
imshow®;
%以模版左下角为原点建立坐标系
m1=m-84;
n1=n-40;
%换成毫米
m1=m1100/256;
n1=n1100/256;
zuobiao=[m1,n1];

程序三
a=input(‘输入您想看第几问的结果=’);
if(a1)
load(‘DATA2.mat’)
R=DATA2;
end
if(a2)
load(‘DATA3.mat’)
R=DATA3;
end
if(a==3)
load(‘DATA5.mat’)
R=DATA5;
end
figure;imshow(R,[]);
%直接反投影法
s= pow2(nextpow2(size(R,1)));%重构图像的大小
P1 = zeros(s,s);%用于存放重构后的图像
for i=1:size(R,2)
SS = imrotate( repmat(R(:,i),1,size(R,1)),i-1,‘bilinear’);
SS = SS(floor(size(SS,1)/2-s/2)+1:floor(size(SS,1)/2+s/2),floor(size(SS,2)/2-s/2)+1:floor(size(SS,2)/2+s/2));
P1=P1+SS;
end
P1=P1/size(R,2);
P1=rot90(P1);
%将512512变换本题所要求的256256
j=0;
S=ones(256,512);
X=ones(256,256);
for i=1:2:512
j=j+1;
S(j,:)=(P1(i,:)+P1(i+1,:))/2;
end
j=0;
for i=1:2:512
j=j+1;
X(:,j)=(S(:,i)+S(:,i+1))/2;
end
figure;imshow(X,[]);title(‘直接反投影法’);

程序四
a=input(‘输入您想看第四问第几个图的结果=’);
if(a1)
load(‘DATA2.mat’)
R=DATA2;
end
if(a2)
load(‘DATA3.mat’)
R=DATA3;
end
if(a3)
load(‘DATA5.mat’)
R=DATA5;
end
N=180;
%滤波
Z=size(R,1);
F=zeros((Z*2-1),1);
for i=0:Z-1
if i0
F(Z-i)=1/4;
elseif rem(i,2)==0
F(Z-i)=0;
F(Z+i)=0;
else
F(Z-i)=-1/(ipi)^2;
F(Z+i)=-1/(ipi)^2;
end
end
W=zeros(Z,N);
for i=1:N
s=R(:, i);
ZZ=conv(s’,F’);
W(:,i)=ZZ(Z:2Z-1);
end
figure;imshow(W,[]);
%直接反投影法
l = pow2(nextpow2(size(W,1)));%重构图像的大小
P2 = zeros(l,l);%用于存放重构后的图像
for i=1 : size(W,2)
SS = imrotate( repmat(W(:,i),1,size(W,1)),i-1,‘bilinear’ );
SS = SS(floor(size(SS,1)/2-l/2)+1:floor(size(SS,1)/2+l/2),floor(size(SS,2)/2-l/2)+1:floor(size(SS,2)/2+l/2));
P2=P2+SS;
end
P2=P2/size(W,1);
P2=rot90(P2);
%将512512变换本题所要求的256*256
S=ones(256,512);
X=ones(256,256);
j=0;
for i=1:2:512
j=j+1;
S(j,:)=(P2(i,:)+P2(i+1,:))/2;
end
j=0;
for i=1:2:512
j=j+1;
X(:,j)=(S(:,i)+S(:,i+1))/2;
end
figure;imshow(X,[]);title(‘滤波反投影法’);

程序五
%用phantom函数可以获得仿体图像；
%用randon可获得不同角度的一维投影；
P = phantom(‘Modified Shepp-Logan’,256);
R=radon§;
figure;imshow(R,[]);
figure;
imshow(P,[]);title(‘仿体图’);
%直接反投影法
L = pow2(nextpow2(size(R,1))-1);%重构图像的大小
P1 = zeros(L,L);%用于存放重构后的图像
for i=1:size(R,2)
SS = imrotate( repmat(R(:,i),1,size(R,1)),i-1,‘bilinear’ );
SS = SS(floor(size(SS,1)/2-L/2)+1:floor(size(SS,1)/2+L/2),floor(size(SS,2)/2-L/2)+1:floor(size(SS,2)/2+L/2));
P1=P1+SS;
end
P1=P1/size(R,1);
P1=rot90(P1);
figure;imshow(P1,[]);title(‘直接反投影法’)
%滤波反投影法
N=180;
%滤波
Z=size(R,1);
F=zeros((Z2-1),1);
for i=0:Z-1
if i==0
F(Z-i)=1/4;
elseif rem(i,2)==0
F(Z-i)=0;
F(Z+i)=0;
else
F(Z-i)=-1/(ipi)^2;
F(Z+i)=-1/(ipi)^2;
end
end
W=zeros(Z,N);
for i=1:N
s=R(:,i);
ZZ=conv(s’,F’);
W(:,i)=ZZ(Z:2Z-1);
end
%反投影
P3=zeros(L,L);
for i=1:L
for j=1:L
for k=1:180
N=k/180*pi;
T=(j-L/2-0.5)*cos(N)+(L/2+0.5-i)*sin(N)+(Z+1)/2;
T1=floor(T);
T2=floor(T+1);
P3(i,j)=P3(i,j)+(T2-T)*W(T1,k)+(T-T1)W(T2,k);
end
end
end
P3=pi/NP3;
figure;imshow(P3,[]);title(‘滤波反投影法’);

程序六
load(‘problem2.mat’)
load(‘problem3.mat’)
load(‘DATA4.mat’)
N1=ones(10,1);
N2=ones(10,1);
for i=1:10
m=round(((DATA4(i,1)-39.4531)3^0.50.5)*1.7222+128);
n=round(((DATA4(i,2)-57.0313)*0.5)*1.7222+128);
N1(i,1)=problem2(m,n);
N2(i,1)=problem3(m,n);
end