深入理解spark优化器

目前的优化方法主要有：

一、spark优化方法介绍

一阶

• Gradient Descent 梯度下降
• Stochastic Gradient Descent 随机梯度下降

二阶

• Limited-memory BFGS（有限内存的拟牛顿法）
  

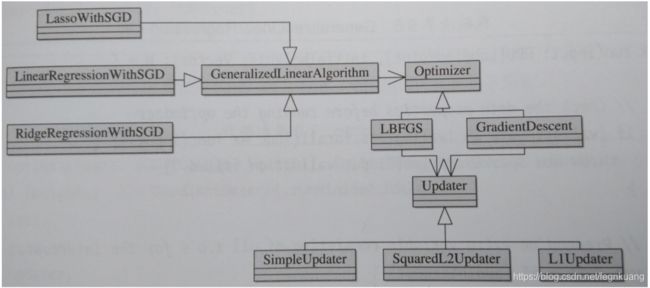
二、spark优化类图

三、源码分析

1. spark mllib的optimization代码结构

optimization

Gradient -- 抽象类

LogisticGradient

LeastSquaresGradient

HingeGradient

GradientDescent

LBFGS

NNLS -- 非负最小二乘

Optimizer

Updater

• NNLS: 使用改进投影梯度法结合共轭梯度法来求解非负最小二乘

2. GradientDescent.scala代码分析
   梯度下降默认采用SGD方法。其中涉及到的矩阵向量运算spark调用了breeze库来执行。

package org.apache.spark.mllib.optimization

import scala.collection.mutable.ArrayBuffer

import breeze.linalg.{norm, DenseVector => BDV}

import org.apache.spark.annotation.DeveloperApi
import org.apache.spark.internal.Logging
import org.apache.spark.mllib.linalg.{Vector, Vectors}
import org.apache.spark.rdd.RDD


/**
 * 利用梯度下降求解最优化问题的类
 * @param gradient 梯度函数.
 * @param updater 用于每次迭代后更新权重的更新器.
 */
class GradientDescent private[spark] (private var gradient: Gradient, private var updater: Updater)
  extends Optimizer with Logging {

  private var stepSize: Double = 1.0
  private var numIterations: Int = 100
  private var regParam: Double = 0.0
  private var miniBatchFraction: Double = 1.0
  private var convergenceTol: Double = 0.001

  /**
   * SGD初始化步长，默认1.0
   * In subsequent steps, the step size will decrease with stepSize/sqrt(t)
   */
  def setStepSize(step: Double): this.type = {
    require(step > 0,
      s"Initial step size must be positive but got ${step}")
    this.stepSize = step
    this
  }

  /**
   * 设置SGD每次迭代的数据采样比.
   * Default 1.0 (corresponding to deterministic/classical gradient descent)
   */
  def setMiniBatchFraction(fraction: Double): this.type = {
    require(fraction > 0 && fraction <= 1.0,
      s"Fraction for mini-batch SGD must be in range (0, 1] but got ${fraction}")
    this.miniBatchFraction = fraction
    this
  }

  /**
   * 设置SGD迭代次数，默认100.
   */
  def setNumIterations(iters: Int): this.type = {
    require(iters >= 0,
      s"Number of iterations must be nonnegative but got ${iters}")
    this.numIterations = iters
    this
  }

  /**
   * 设置正则参数，默认0.0.
   */
  def setRegParam(regParam: Double): this.type = {
    require(regParam >= 0,
      s"Regularization parameter must be nonnegative but got ${regParam}")
    this.regParam = regParam
    this
  }

  /**
   * 设置收敛误差. Default 0.001
   * 用于判断迭代终止条件.
   * 遵循以下逻辑：
   *
   *  - If the norm of the new solution vector is greater than 1, the diff of solution vectors
   *    is compared to relative tolerance which means normalizing by the norm of
   *    the new solution vector.
   *  - If the norm of the new solution vector is less than or equal to 1, the diff of solution
   *    vectors is compared to absolute tolerance which is not normalizing.
   *
   * Must be between 0.0 and 1.0 inclusively.
   */
  def setConvergenceTol(tolerance: Double): this.type = {
    require(tolerance >= 0.0 && tolerance <= 1.0,
      s"Convergence tolerance must be in range [0, 1] but got ${tolerance}")
    this.convergenceTol = tolerance
    this
  }

  /**
   * Set the gradient function (of the loss function of one single data example)
   * to be used for SGD.
   */
  def setGradient(gradient: Gradient): this.type = {
    this.gradient = gradient
    this
  }


  /**
   * Set the updater function to actually perform a gradient step in a given direction.
   * 设置更新器函数，用于按照给定方向计算下降梯度，还可以在其中制定正则项
   * The updater is responsible to perform the update from the regularization term as well,
   * and therefore determines what kind or regularization is used, if any.
   */
  def setUpdater(updater: Updater): this.type = {
    this.updater = updater
    this
  }

  /**
   * :: DeveloperApi ::
   * Runs gradient descent on the given training data.
   * @param data training data
   * @param initialWeights initial weights
   * @return solution vector
   */
  @DeveloperApi
  def optimize(data: RDD[(Double, Vector)], initialWeights: Vector): Vector = {
    val (weights, _) = GradientDescent.runMiniBatchSGD(
      data,
      gradient,
      updater,
      stepSize,
      numIterations,
      regParam,
      miniBatchFraction,
      initialWeights,
      convergenceTol)
    weights
  }

}

/**
 * :: DeveloperApi ::
 * Top-level method to run gradient descent.
 */
@DeveloperApi
object GradientDescent extends Logging {
  /**
   * 使用小批量数据样本并行运行SGD
   * 每次迭代中，对所有数据进行采样，求解近似梯度
   * 每次迭代都要进行数据抽样，并计算数据抽样子集上的梯度平均值
   *
   * @param data 所有的输入数据. RDD格式, 每条数据格式为(label, [feature values]).
   * @param gradient Gradient 对象，用于计算单样本的损失函数的梯度
   * @param updater更新器函数按照给定方向计算下降梯度.
   * @param stepSize 第一步的初始步长
   * @param numIterations 迭代次数.
   * @param regParam 正则项参数
   * @param miniBatchFraction 每次迭代中数据抽样的比率，默认是1.0.
   * @param convergenceTol 迭代结束条件，计算当前权重和上次权重的相对差值，计算时用到了L2范式，默认值是0.001.
   * @return 返回一个二元组. 第一个元素是包含每个特征权重的列向量，第二个是包含每次迭代的随机损失的数组。
   */
  def runMiniBatchSGD(
      data: RDD[(Double, Vector)],
      gradient: Gradient,
      updater: Updater,
      stepSize: Double,
      numIterations: Int,
      regParam: Double,
      miniBatchFraction: Double,
      initialWeights: Vector,
      convergenceTol: Double): (Vector, Array[Double]) = {

    // convergenceTol should be set with non minibatch settings
    if (miniBatchFraction < 1.0 && convergenceTol > 0.0) {
      logWarning("Testing against a convergenceTol when using miniBatchFraction " +
        "< 1.0 can be unstable because of the stochasticity in sampling.")
    }

    if (numIterations * miniBatchFraction < 1.0) {
      logWarning("Not all examples will be used if numIterations * miniBatchFraction < 1.0: " +
        s"numIterations=$numIterations and miniBatchFraction=$miniBatchFraction")
    }

    val stochasticLossHistory = new ArrayBuffer[Double](numIterations)
    // Record previous weight and current one to calculate solution vector difference

    var previousWeights: Option[Vector] = None
    var currentWeights: Option[Vector] = None

    val numExamples = data.count()

    // if no data, return initial weights to avoid NaNs
    if (numExamples == 0) {
      logWarning("GradientDescent.runMiniBatchSGD returning initial weights, no data found")
      return (initialWeights, stochasticLossHistory.toArray)
    }

    if (numExamples * miniBatchFraction < 1) {
      logWarning("The miniBatchFraction is too small")
    }

    // Initialize weights as a column vector
    var weights = Vectors.dense(initialWeights.toArray)
    val n = weights.size

    /**
     * 第一次迭代时，如果是L2范式，regVal 初始化为权重参数的平方之和
     */
    var regVal = updater.compute(
      weights, Vectors.zeros(weights.size), 0, 1, regParam)._2

    var converged = false // indicates whether converged based on convergenceTol
    var i = 1
    while (!converged && i <= numIterations) {
      val bcWeights = data.context.broadcast(weights)
      // 数据抽样
      // 计算，对该抽样集上的样本的子梯度进行求和，包含一次map-reduce操作。
      这里求和采用了treeAggregate而不是aggregate，
      主要是通过预reduce在性能上进行优化，
      可以并行求和，防止直接reduce带来的OOM问题。
      val (gradientSum, lossSum, miniBatchSize) = data.sample(false, miniBatchFraction, 42 + i)
        .treeAggregate((BDV.zeros[Double](n), 0.0, 0L))(
          seqOp = (c, v) => {
            // c: (grad, loss, count), v: (label, features)
            val l = gradient.compute(v._2, v._1, bcWeights.value, Vectors.fromBreeze(c._1))
            (c._1, c._2 + l, c._3 + 1)
          },
          combOp = (c1, c2) => {
            // c: (grad, loss, count)
            (c1._1 += c2._1, c1._2 + c2._2, c1._3 + c2._3)
          })
      bcWeights.destroy()

      if (miniBatchSize > 0) {
        /**
         * lossSum is computed using the weights from the previous iteration
         * and regVal is the regularization value computed in the previous iteration as well.
         */
        stochasticLossHistory += lossSum / miniBatchSize + regVal
        val update = updater.compute(
          weights, Vectors.fromBreeze(gradientSum / miniBatchSize.toDouble),
          stepSize, i, regParam)
        weights = update._1
        regVal = update._2

        previousWeights = currentWeights
        currentWeights = Some(weights)
        if (previousWeights != None && currentWeights != None) {
          converged = isConverged(previousWeights.get,
            currentWeights.get, convergenceTol)
        }
      } else {
        logWarning(s"Iteration ($i/$numIterations). The size of sampled batch is zero")
      }
      i += 1
    }

    logInfo("GradientDescent.runMiniBatchSGD finished. Last 10 stochastic losses %s".format(
      stochasticLossHistory.takeRight(10).mkString(", ")))

    (weights, stochasticLossHistory.toArray)

  }

  /**
   * Alias of `runMiniBatchSGD` with convergenceTol set to default value of 0.001.
   */
  def runMiniBatchSGD(
      data: RDD[(Double, Vector)],
      gradient: Gradient,
      updater: Updater,
      stepSize: Double,
      numIterations: Int,
      regParam: Double,
      miniBatchFraction: Double,
      initialWeights: Vector): (Vector, Array[Double]) =
    GradientDescent.runMiniBatchSGD(data, gradient, updater, stepSize, numIterations,
                                    regParam, miniBatchFraction, initialWeights, 0.001)


  private def isConverged(
      previousWeights: Vector,
      currentWeights: Vector,
      convergenceTol: Double): Boolean = {
    // To compare with convergence tolerance.
    val previousBDV = previousWeights.asBreeze.toDenseVector
    val currentBDV = currentWeights.asBreeze.toDenseVector

    // This represents the difference of updated weights in the iteration.
    val solutionVecDiff: Double = norm(previousBDV - currentBDV)

    solutionVecDiff < convergenceTol * Math.max(norm(currentBDV), 1.0)
  }

}