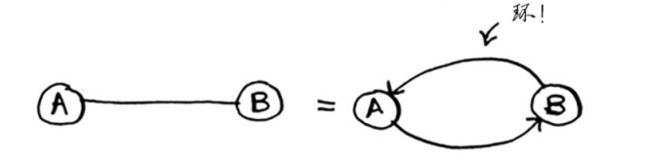《算法图解》学习笔记习题和代码（第七章 狄克斯特拉算法）Python3

目录

第七章 狄克斯特拉算法

7.1 使用狄克斯特拉算法 

7.2 术语  

7.3换钢琴 （狄克斯特拉算法的一个例子）

7.4 负权边 

7.5 代码实现 

练习 

7.6 小结

---

第七章 狄克斯特拉算法

狄克斯特拉算法 （Dijkstra’s algorithm）

上一章介绍了图的概念，这一章引入加权图。还拿上一章内容举例：

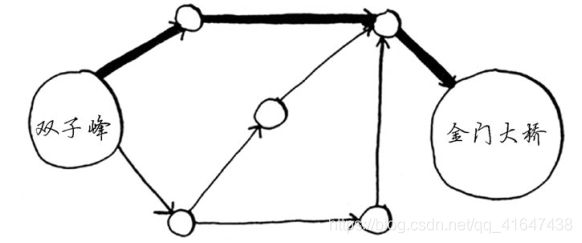
我们使用广度优先搜索，找到的最短路径是路段数最短。（下图加粗路线）那是最快路径吗？

给每一条到达金门大桥的路线加上时间，如下图：（加权图）

 此时，到达金门大桥最快的方式如上图加粗路线所示，而不是第一幅图的最短路径。这就是一个简单的加权图的例子。

广度优先搜索，它找出的是段数最少的路径。要找出最快的路径（如第二个图所示），该如何办呢？为此，可使用另一种算法——狄克斯特拉算法（Dijkstra’s algorithm）。 

7.1 使用狄克斯特拉算法 

狄克斯特拉算法包含4个步骤。
(1) 找出开销最少的节点，即可在最短时间内到达的节点。 
(2) 更新该节点的邻居的开销，其含义将稍后介绍。 
(3) 重复这个过程，直到对图中的每个节点都这样做了。 
(4) 计算最终路径。

 

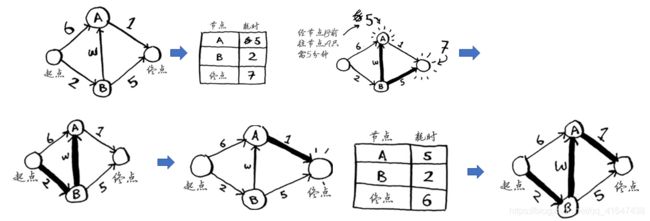
第一步：找出开销最少的节点。（是去A还是B） 去B只要两分钟，去B。

第二步：计算经节点B前往其各个邻居所需的时间（更新B的邻居开销）。 从B去A，去终点哪个开销少。去A只要三分钟。

（表格里的时间算上了第一步的时间）

第三步：重复！

更新节点A的所有邻居的开销。

最终可找到最短路径，如果使用广度优先搜索，找到的最短路径将不是这条，因为这条路径包含3段，而有一条从起点到终点的路径只有两段。

在狄克斯特拉算法中，你给每段都分配了一个数字或权重，因此狄克斯特拉算法找出的是总权重最小的路径。 

7.2 术语  

每条边有关联数字的图，这些数字称为权重（weight）。

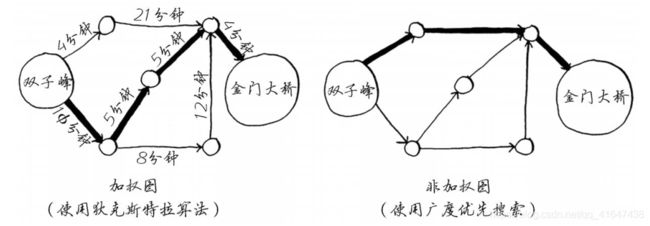
带权重的图称为加权图（weighted graph），不带权重的图称为非加权图（unweighted graph）。 

非加权图中的最短路径，可使用广度优先搜索。 加权图中的最短路径，可使用狄克斯特拉算法。

图还可能有环：

从一个节点出发，走一圈后又回到这个节点。 因此，绕环的路径不可能是最短的路径。

要找出上图从起点到终点的最短路径 ，显然绕环前行不合理，增加了权重。

前几章提到的无向图，无向图意味着两个节点彼此指向对方，其实就是环。

 在无向图中，每条边都是一个环。狄克斯特拉算法只适用于有向无环图（directed acyclic  graph，DAG）。 

7.3换钢琴 （狄克斯特拉算法的一个例子）

 

这个图中的节点是大家愿意拿出来交换的东西，边的权重是交换时需要额外加多少钱。比如拿海报换吉他需要额外加30美元。需要确定采用哪种路径将乐谱换成钢琴时需要支付的额外费用最少。为此，可以使用狄克斯特拉算法。

为了计算最短路径，除了计算和更新开销，也更新父节点列表。

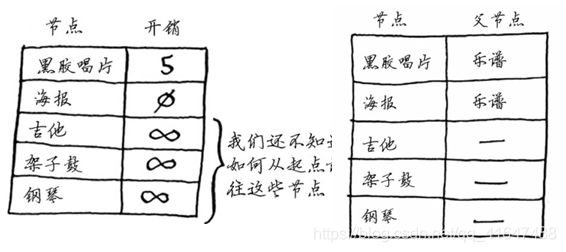
首先，创建一个表格，在其中列出每个节点的开销。为计算最终路径，还需在这个表中添加表示父节点的列。 

第一步：找出最便宜的节点。在这里，换海报最便宜，不需要支付额外的费用。 

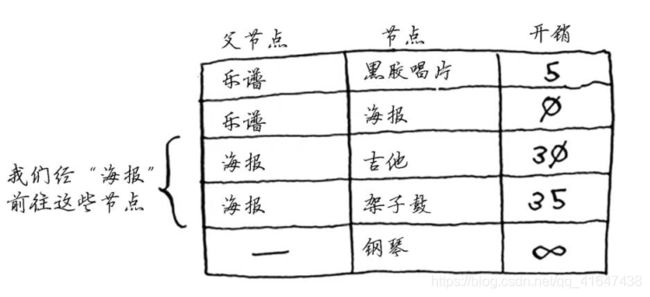
第二步：计算前往该节点各个邻居的开销。 

 此时更新后的结果，从乐谱沿海报到吉他的开销为30美元，最少。（终点钢琴的父节点是吉他和架子鼓，所以这里我们先计算这到达两个父节点的最少开销。）

 再次执行第一步：（从乐谱起点出发）下一个最便宜的节点是黑胶唱片——需要额外支付5美元。 

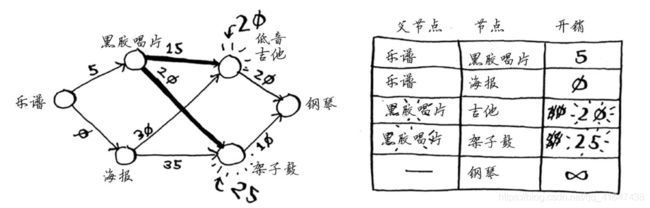
再次执行第二步：更新黑胶唱片的各个邻居的开销。 

乐谱沿黑胶唱片到达吉他、架子鼓的开销在上图中更新。其中到达吉他的开销最少，为20美元。因此将这些乐器的父节点改为黑胶唱片。 （经过分析，在海报和黑胶唱片的路线中选择了黑胶唱片的路线）

现在确定了乐谱->黑胶唱片->吉他的路线。

下一个最便宜的是吉他，因此更新其邻居的开销。 

 这里计算出了吉他换钢琴的开销为40美元（从起点到终点的总开销），于是将其父节点设置为吉他。

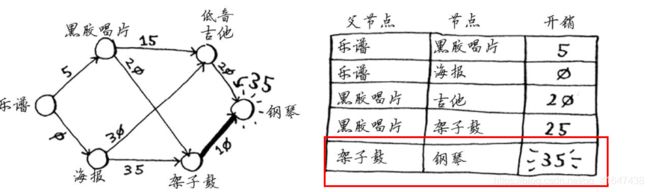
下一个便宜的节点是黑胶唱片，更新其邻居的开销。 （计算从黑胶唱片到钢琴）

用架子鼓换钢琴，付出的费用更少，为35美元。

因此，最便宜的交换路径为乐谱->黑胶唱片->架子鼓->钢琴  付出的费用为35美元。

我们知道最短路径的开销为35美元，但如何确定这条路径呢？为此，先找出钢琴的父节点。 接着就沿着路线一路找父节点，就确定出了最短路径。

最短路径指的并不一定是物理距离，也可能是让某种度量指标最小。在这个示例中，最短路径指的是从乐谱换到钢琴，额外支付的费用最少。

7.4 负权边 

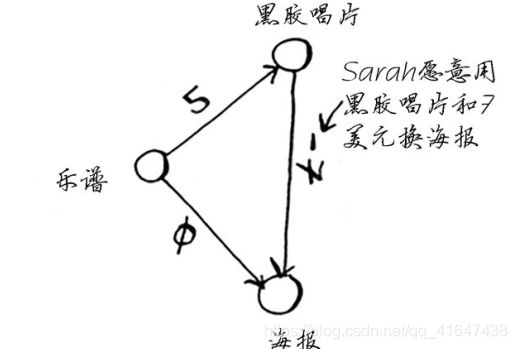
不但不用支付额外的费用，还可得7美元。从黑胶唱片到海报的边的权重为负！即这种交换不仅不用花钱还能够得到7美元。

现在Rama有两种方式可以得到海报，如下图所示： 

 第二种方式更划算——Rama可赚2美元！

最终Rama想换到架子鼓，采用第二种路线（方式），就可以节省两美元了。

 

如果对这个图运行狄克斯特拉算法，Rama将选择错误的路径——更长的那条路径。如果有负权边，就不能使用狄克斯特拉算法。因为负权边会导致这种算法不管用。 这是为什么？对上图执行狄克斯特拉算法。

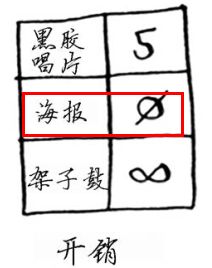
第一步，从起点开始找到 开销最低的节点。

 根据狄克斯特拉算法，没有比不支付任何费用获得海报更便宜的方式。（你知道这并不对！前面的第二种方式获取海报开销更少，但经过了两段路程）无论如何，我们来更新其邻居（就是架子鼓）的开销。 

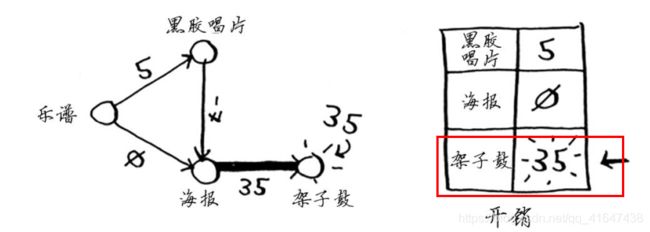
现在，架子鼓的开销变成了35美元。下一步，我们来找出最便宜的未处理节点。  （海报已经处理过了）

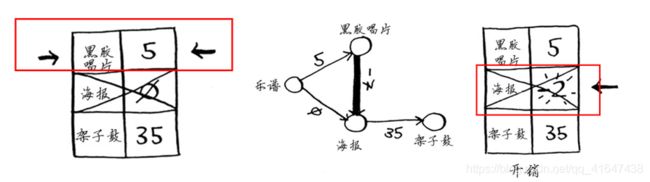
下一个最便宜的未处理节点是黑胶唱片。更新它的邻居的开销。黑胶唱片的邻居是海报！而海报节点已处理过，这里却更新了它的开销。这是一个危险信号。节点一旦被处理，就意味着没有前往该节点的更便宜途径，但你刚才却找到了前往海报节点的更便宜途径！架子鼓没有任何邻居，因此算法到此结束，最终换得架子鼓的开销为35美元。

因为狄克斯特拉算法这样假设：对于处理过的海报节点，没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。因此，不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼-福德算法（Bellman-Ford  algorithm）。 

7.5 代码实现 

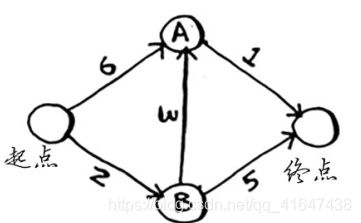
如何使用代码来实现狄克斯特拉算法，这里以下面的图为例。 

要编写解决这个问题的代码，需要三个散列表。  

随着算法的进行，你将不断更新散列表costs和parents。

下面代码构建了一个包含散列表的散列表，如下图所示。

graph = {}
graph['start'] = {}
graph['start']['a'] = 6
graph['start']['b'] = 2
print(graph['start'].keys())#查看起点的邻居节点
print(graph['start']['a'])#查看到从起点到a的边权重
print(graph['start']['b'])#查看到从起点到b的边权重

OUT:
dict_keys(['a', 'b'])
6
2

 下面代码，添加其他节点的邻居，完善这个图：

#添加其他节点及其邻居
graph["a"] = {} 
graph["a"]["end"] = 1 

graph["b"] = {} 
graph["b"]["a"] = 3 
graph["b"]["end"] = 5 

graph["end"] = {} #终点没有邻居

 下一步，1.用一个散列表来存储每个节点的开销。 对于还不知道的开销，你将其设置为无穷大：infinity = float("inf") 

2.创建存储父节点的散列表。

3.创建一个数组，用于记录处理过的节点。

#创建一个存储开销的散列表
infinity = float("inf") 
costs = {} 
costs["a"] = 6 
costs["b"] = 2 
costs["end"] = infinity 

#存储父节点的散列表
parents = {} 
parents["a"] = "start" 
parents["b"] = "start" 
parents["end"] = None 

#需要一个数组，用于记录处理过的节点
processed = [] 

算法流程图：

def find_lowest_cost_node(costs):
    lowest_cost = float('inf')
    lowest_cost_node = None
    
    for node in costs:    #遍历所有节点
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_cost_node = node 
    return lowest_cost_node

node = find_lowest_cost_node(costs)      #从开销的散列表中找到最便宜的节点

while node is not None:      #所有节点都被处理过后，while循环会终止
    cost = costs[node]     #最便宜节点的开销
    neighbors = graph[node]
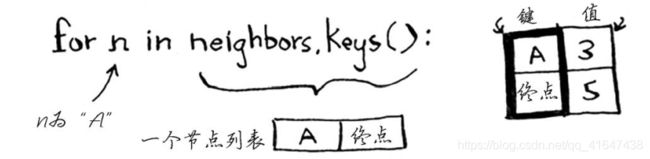
    for n in neighbors.keys():  #遍历这个节点所有的邻居
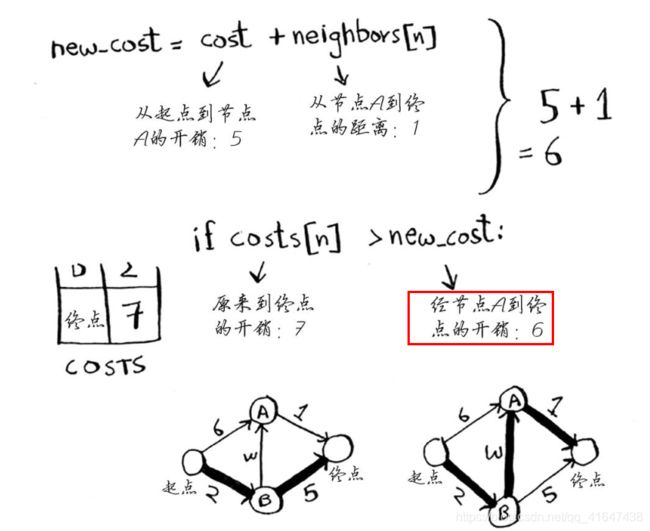
        new_cost = cost + neighbors[n] #经过当前最便宜节点到达它的邻居的开销
        if costs[n] > new_cost:       #如果经过该节点到达邻居的开销比之前开销列表中这个邻居的开销少，就更新该邻居的开销
            costs[n] = new_cost
            parents[n] = node              #再更新这个邻居节点的父节点为当前节点
    processed.append(node)           #标记处理过的点
    node = find_lowest_cost_node(costs) #找下一个开销最少的点，进行下一个while循环

print('到达终点最短距离为：',costs['end'])
parents

OUT:

到达终点最短距离为： 6
{'a': 'b', 'b': 'start', 'end': 'a'}

上面的代码实现过程图解：

第一步，在开销列表找出开销最低的节点：

第二步，获取该节点的开销和邻居。  

遍历邻居。更新邻居的开销。

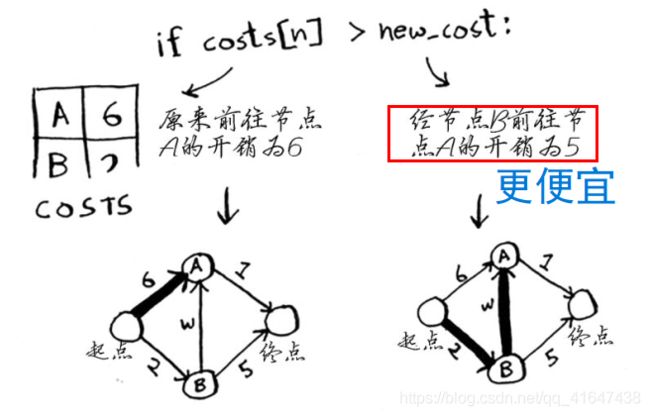
每个节点都有开销。开销指的是从起点前往该节点需要多长时间。在这里，你计算从起点出发，经节点B前往节点A（而不是直接前往节点A）需要多长时间。 

接着对新旧开销进行比较。

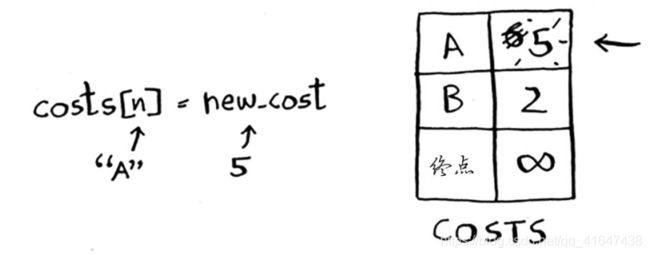
因此更新节点A的开销。 

 这条新路径经由节点B，因此节点A的父节点改为节点B。 

现在回到了for循环开头。B的下一个邻居是终点节点。经节点B前往终点需要多长时间呢？  

现在计算出由B到终点的开销为7分钟，终点原来的开销为无穷大，比7分钟长。 

我们更新终点的节点开销，并更新其父节点。

你更新了节点B的所有邻居的开销。现在，将节点B标记为处理过。 

 接下来找下一个最便宜的未处理节点。就是A

获取节点A的开销和邻居。 节点A只有一个邻居：终点节点。 

如果经节点A前往终点，需要多长时间呢？ 6分钟，比由B到达终点的7分钟短，因此我们更新终点的开销和父节点。

练习 

7.1 在下面的各个图中，从起点到终点的最短路径的总权重分别是多少？ 

答：

A：8     B：60       C使用狄克斯特拉算法无法找出最短路径，因为存在负权边。

7.6 小结

广度优先搜索用于在非加权图中查找最短路径。
狄克斯特拉算法用于在加权图中查找最短路径。
仅当权重为正时狄克斯特拉算法才管用。
如果图中包含负权边，请使用贝尔曼 福德算法。

避免绕环路径