softmax与sigmoid, 交叉熵,多分类与多标签分类
https://www.cnblogs.com/nopassword/p/8192474.html
一:什么是softmax?
在机器学习尤其是深度学习中,softmax是个非常常用而且比较重要的函数,尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数,并且归一化保证和为1,因此多分类的概率之和也刚好为1。
首先我们简单来看看softmax是什么意思。顾名思义,softmax由两个单词组成,其中一个是max。对于max我们都很熟悉,就是取所有给定的数字的最大值。
另外一个单词为soft。max存在的一个问题是什么呢?如果将max看成一个分类问题,就是非黑即白,最后的输出是一个确定的变量。更多的时候,我们希望输出的是取到某个分类的概率,或者说,我们希望分值大的那一项被经常取到,而分值较小的那一项也有一定的概率偶尔被取到,所以我们就应用到了soft的概念,即最后的输出是每个分类被取到的概率。
![]()
这张图的等号左边部分就是全连接层做的事,W是全连接层的参数,我们也称为权值,X是全连接层的输入,也就是特征。从图上可以看出特征X是N*1的向量,这是怎么得到的呢?这个特征就是由全连接层前面多个卷积层和池化层处理后得到的,假设全连接层前面连接的是一个卷积层,这个卷积层的输出是100个特征(也就是我们常说的feature map的channel为100),每个特征的大小是4*4,那么在将这些特征输入给全连接层之前会将这些特征flat成N*1的向量(这个时候N就是100*4*4=1600)。解释完X,再来看W,W是全连接层的参数,是个T*N的矩阵,这个N和X的N对应,T表示类别数,比如你是7分类,那么T就是7。我们所说的训练一个网络,对于全连接层而言就是寻找最合适的W矩阵。因此全连接层就是执行WX得到一个T*1的向量(也就是图中的logits[T*1]),这个向量里面的每个数都没有大小限制的,也就是从负无穷大到正无穷大。然后如果你是多分类问题,一般会在全连接层后面接一个softmax层,这个softmax的输入是T*1的向量,输出也是T*1的向量(也就是图中的prob[T*1],这个向量的每个值表示这个样本属于每个类的概率),只不过输出的向量的每个值的大小范围为0到1。
现在你知道softmax的输出向量是什么意思了,就是概率,该样本属于各个类的概率!
那么softmax执行了什么操作可以得到0到1的概率呢?先来看看softmax的公式
![]()
公式非常简单,前面说过softmax的输入是WX(为TX1的向量),假设模型的输入样本是I,讨论一个3分类问题(类别用1,2,3表示),样本I的真实类别是2,那么这个样本I经过网络所有层到达softmax层之前就得到了WX,也就是说WX是一个3*1的向量,那么上面公式中的aj就表示这个3*1的向量中的第j个值(最后会得到S1,S2,S3);而分母中的ak则表示3*1的向量中的3个值,所以会有个求和符号(这里求和是k从1到T,T和上面图中的T是对应相等的,也就是类别数的意思,j的范围也是1到T)。因为e^x恒大于0,所以分子永远是正数,分母又是多个正数的和,所以分母也肯定是正数,因此Sj是正数,而且范围是(0,1)。如果现在不是在训练模型,而是在测试模型,那么当一个样本经过softmax层并输出一个T*1的向量时,就会取这个向量中值最大的那个数的index作为这个样本的预测标签。
因此我们训练全连接层的W的目标就是使得其输出的WX在经过softmax层计算后其对应于真实标签的预测概率要最高。
举个例子:假设你的WX=[3,1,-3],给一个图,这个图比较清晰地告诉大家softmax是怎么计算的。
![]()
step1:
那么经过softmax层后就会得到[0.88,0.12,0.002],这三个数字表示这个样本属于第1,2,3类的概率分别是0.88,0.12,0。
注意:此处的e,是自然对数函数的底数,是一个数学常数,数值约为e ≈ 2.71828,其中一种定义方式为:
上图的计算过程
import math
a=math.exp(3)
b=math.exp(1)
c=math.exp(-3)
he=a+b+c
z1=a/he
z2=b/he
z3=c/he
print(a,b,c)
#(20.085536923187668, 2.718281828459045, 0.049787068367863944)
print(z1,z2,z3)
#(0.878878242732151, 0.11894323591065209, 0.0021785213571970234)有了softmax之后,再来看交叉熵
二:什么是交叉熵?
交叉熵是一个信息论中的概念,它原来是用来估算平均编码长度的,给定两个概率分布p和q,通过q来表示p的交叉熵为
注意:交叉熵刻画的是两个概率分布之间的距离,或可以说它刻画的是通过概率分布q来表达概率分布p的困难程度,p一般代表正确答案(就是真实值y_true或y), q代表的是预测值(就是神经网络的预测值y_pre或![]() ),交叉熵越小,代表两个概率的分布越接近,或者可以说预测值预测的结果很好,如实表达了真实值.
),交叉熵越小,代表两个概率的分布越接近,或者可以说预测值预测的结果很好,如实表达了真实值.
那么在神经网络中,怎样把前向传播得到的结果也变成概率分布呢?softmax回归就是一个常用的方法(所以面试官经常问你,为什么交叉熵经常和softmax一起使用?)
还是借用上面的例子,假设有一个3分类问题,某个样本的正确答案是(1,0,0),这个样本经过神经网络模型softmax回归之后的预测答案是[0.88,0.12,0.002],那么预测答案和正确答案之间的交叉熵就为:
H(y_true,y_pre)=-[1*log0.88+0*log0.12+0*log0.002)=0.05
特殊情形:
有一类比较特殊的问题,比如投掷硬币只有两种可能,字朝上或花朝上,买彩票只有两种可能,中奖或不中奖,我们称之为0-1分布问题(二项分布的特例),对于这类问题,熵的计算方法可以简化为如下算式:
考虑到二分类问题中有
![]()
则上式可化简为:
![]()
sigmoid 激活函数
则上公式:
![]()
作用:用于二分类。
多类分类及多标签分类
多类分类:
数据集是一个多分类,而不仅仅是二分类,不是“是与否”问题,而是属于多类中的哪一类的问题,一个样本属于且只属于多个分类中的一个,一个样本只能属于一个类,不同类之间是互斥的。举例而言,MNIST数据集,常用的数字手写体识别数据集,它的标签是一个多分类的过程,要将数字手写体识别为0-9中的某一个数字。
多标签分类:
一个样本的标签不仅仅局限于一个类别,可以具有多个类别,不同类之间是有关联的,比如一件一副,其具有的特征类别有长袖,蕾丝等属性,这两个属性标签不是互斥的,而是有关联的。
softmax激活函数应用于多类分类,sigmoid激活函数一般不用来做多类分类,而是用来做二分类,这一属性使得其适合应用于多标签分类。多标签分类中,大多使用binary-crossentropy损失函数。

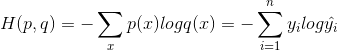
![H(p,q)=H(x)=-\sum _{i=1}^2y_ilog\hat{y_i}=-[y_1log\hat{y_1}+y_2log\hat{y_2}])](http://img.e-com-net.com/image/info8/cdee00f3c430494d9611bda8295d9b92.gif)