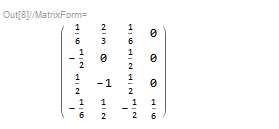三维空间的贝塞尔曲线、B样条线分段拟合---mathematica

待拟合三维数据

path = {
     {
     30, 0, 0}, {
     30 + 14/Sqrt[249], 20/Sqrt[249], 20/Sqrt[
    249]}, {
     32.20470703921131`, 1.3906289084343317`, 
    2.7671279831555884`}, {
     33.09192098994558`, 2.6580774094832877`, 
    4.034576484204544`}, {
     33.11954143398565`, 2.9390588704641174`, 
    6.014547829869958`}, {
     32.50729927398154`, 4.456873016879327`, 
    7.164069362706715`}, {
     33.39451322471581`, 5.724321517928283`, 
    8.431517863755671`}, {
     34.56600017798742`, 5.876252184970187`, 
    10.045375165603202`}, {
     35.56858636708187`, 7.606803929329527`, 
    10.048780093195823`}, {
     36.45580031781614`, 8.874252430378483`, 
    11.316228594244778`}};

定义

根据定义，提取t的系数列表


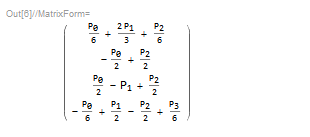
使用梯度—提取P相关的系数矩阵

A = Grad[coe, Table[Subscript[P, i], {
     i, 0, len}]];

添加节点

path1 = Prepend[path, (path[[1]] - path[[2]]) + path[[1]]];
path1 = Append[path1, Last[path] + (Last[path] - path[[-2]])];

关于时间t的表达式

v = Table[
  basis.A.Take[path1, {
     i, i + len}] // N, {i, 1, Length[path1] - len}]

最终拟合
完整代码

If[Length[Names["`*"]] > 0, Remove["`*"]];
(*空间拟合样点*)
path = {
     {
     30, 0, 0}, {
     30 + 14/Sqrt[249], 20/Sqrt[249], 20/Sqrt[
    249]}, {
     32.20470703921131`, 1.3906289084343317`, 
    2.7671279831555884`}, {
     33.09192098994558`, 2.6580774094832877`, 
    4.034576484204544`}, {
     33.11954143398565`, 2.9390588704641174`, 
    6.014547829869958`}, {
     32.50729927398154`, 4.456873016879327`, 
    7.164069362706715`}, {
     33.39451322471581`, 5.724321517928283`, 
    8.431517863755671`}, {
     34.56600017798742`, 5.876252184970187`, 
    10.045375165603202`}, {
     35.56858636708187`, 7.606803929329527`, 
    10.048780093195823`}, {
     36.45580031781614`, 8.874252430378483`, 
    11.316228594244778`}};
f[n_] := \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 0\), \(n\)]\(Binomial[n, i]*
\*SuperscriptBox[\((1 - t)\), \(n - i\)]*
\*SuperscriptBox[\(t\), \(i\)]*
\*SubscriptBox[\(P\), \(i\)]\)\)   (*贝塞尔曲线定义*)
g[k_, n_] := Subscript[P, k]*1/n! \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 0\), \(n - k\)]\(
\*SuperscriptBox[\((\(-1\))\), \(i\)]*Binomial[n + 1, i]*
\*SuperscriptBox[\((t + n - k - i)\), \(n\)]\)\)(*B样条线定义*)
len = 3;(*维度*)
basis = Table[t^i, {
     i, 0, len}];
(*使用贝塞尔拟合时，注释掉第二个coe*)
coe = CoefficientList[f[len], t]; (*贝塞尔:系数--贝塞尔分段拟合，分段处不光滑*)
coe = CoefficientList[Plus @@ Table[g[i, len], {
     i, 0, len}], 
  t];(*B样条线：系数*)
MatrixForm[coe]
A = Grad[coe, Table[Subscript[P, i], {
     i, 0, len}]];
MatrixForm[A]
path1 = Prepend[path, (path[[1]] - path[[2]]) + path[[1]]];
path1 = Append[path1, Last[path] + (Last[path] - path[[-2]])];
v = Table[
   basis.A.Take[path1, {
     i, i + len}] // N, {i, 1, 
    Length[path1] - len}];
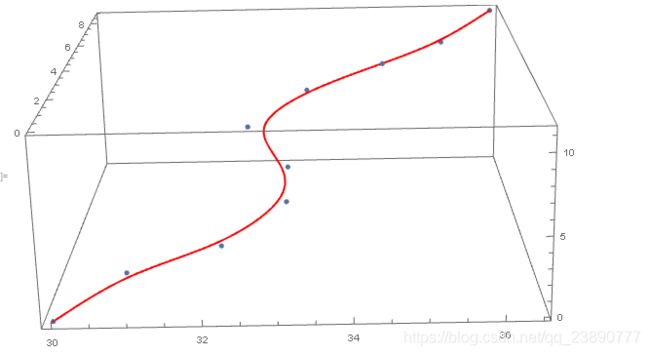
Show[ListPointPlot3D[path, PlotStyle -> PointSize[0.01]], 
 ParametricPlot3D[v, {
     t, 0, 1}, PlotStyle -> Red],
 
 ImageSize -> Large
 ]