堆,栈,队列题型总结
队列(Queue):是限定只能在表的一端进行插入和另一端删除操作的线性表
栈(Stack):是限定之能在表的一端进行插入和删除操作的线性表
算法目录:
- 栈
- 单调栈
- 逆波兰式
- 栈在二叉树中的应用
- 斐波纳契数列实现
- 队列
- 堆
1 优先队列
2 堆排序
一、栈
(一)单调栈
什么是单调栈?
单调栈中的数据存放是有序的,分为单调递增栈与单调递减栈
1.单调递增栈:数据出栈的序列为单调递增序列
2.单调递减栈:数据出栈的序列为单调递减序列
单调递增栈实现步骤:
1.遍历待入栈数组
2.比较栈顶元素与待入栈数据,做出如下判断:
(1)栈空或栈顶元素大于等于当前比较元素: 入栈
(2)栈顶元素小于当前元素:出栈,重复2
举例一(leetcode84)
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积
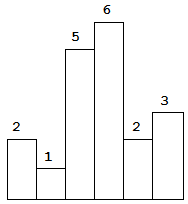
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
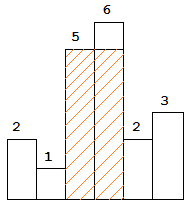
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
思路:
本题采用单调递减栈,对于数据处理分为以下几种情况:
val:当前柱子高度 i:当前柱子位置
1.栈顶元素小于val:i如栈
2.栈顶元素大于val:
栈中大于等于val的值对应的最大面积可求,与max_area做
对比保留最大值
栈中值小于val,则停止元素出栈,并分情况处理:
栈空,则将0如栈,并更新heights[0] = val
栈非空,将最后一个出栈元素last重新如栈,并更新
heights[last] = val
3.栈顶元素等于val: 直接跳过
4.栈为空,待定值直接如栈
遍历结束heights数组后,若栈仍不为空(必定为单调递减栈),单独处理。
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
max_area = 0
stack = []
for i, val in enumerate(heights):
#栈空,入栈
if not stack:
stack.append(i)
#栈顶元素小于如栈元素
elif heights[i] >= heights[stack[-1]]:
stack.append(i)
#栈顶元素大于如栈元素,出栈
else:
j = 0
#求出所有可以确定的最大矩形
while stack and heights[stack[-1]] > heights[i]:
j = stack.pop()
max_area = max(heights[j] * (i - j), max_area)
#更新heights数组
if not stack: j = 0
heights[j] = heights[i]
stack.append(j)
#清空栈,求出所有最大面积
for i in stack:
max_area = max(heights[i] *(len(heights) - i), max_area)
return max_area
(二)逆波兰式(后缀表达式)
中缀表达式转后缀表达式规则:
从左到右遍历中缀表达式中的每个数字与符号,若是数字就输出,即成为后缀表达式一部分,若是符号则判断优先级,是右括号或者优先级低于栈顶符号(乘除优先于加减)则栈顶元素依次出栈并输出,将当前符号进栈,一直到输出后缀表达式为止。
将一个普通的中序表达式转换为逆波兰表达式的一般算法是:
首先需要分配2个栈,一个作为临时存储运算符的栈S1(含一个结束符号),一个作为输入逆波兰式的栈S2(空栈),S1栈可先放入优先级最低的运算符#,注意,中缀式应以此最低优先级的运算符结束。
逐序进行如下步骤:
(1)若取出的字符是操作数,则分析出完整的运算数,该操作数直接送入S2栈
(2)若取出的字符是运算符,则将该运算符与S1栈栈顶元素比较,如果该运算符优先级(不包括括号运算符)大于S1栈栈顶运算符优先级,则将该运算符进S1栈,否则,将S1栈的栈顶运算符弹出,送入S2栈中,直至S1栈栈顶运算符低于(不包括等于)该运算符优先级,最后将该运算符送入S1栈。
(3)若取出的字符是“(”,则直接送入S1栈顶。
(4)若取出的字符是“)”,则将距离S1栈栈顶最近的“(”之间的运算符,逐个出栈,依次送入S2栈,此时抛弃“(”。
(5)重复上面的1~4步,直至处理完所有的输入字符
(6)若取出的字符是“#”,则将S1栈内所有运算符(不包括“#”)逐个出栈,依次送入S2栈。
class Stack():
def __init__(self):
self._stack = []
def pop(self):
return self._stack.pop()
def push(self, x):
self._stack.append(x)
def is_null(self):
return True if not self._stack else False
#中缀表达式转前缀表达式(带括号)
def solve(mid_s):
#定义符号优先级
pro = dict(zip('^*/+-#', [3, 2, 2, 1, 1, 0]))
#前缀栈
suffix_s = Stack()
#保存结果
out = []
suffix_s.push('#')
for c in mid_s:
#左括号直接如栈
if c == '(':
suffix_s.push(c)
#遇到右括号,将括号内部的符号如栈
elif c == ')':
t = suffix_s.pop()
while t != '(':
out.append(t)
t = suffix_s.pop()
#运算符
elif c in '^*/+-':
while True:
t = suffix_s.pop()
#左括号停止判断
if t == '(':
suffix_s.push(t)
break
#将优先级高的符号出栈保存到结果集中
if pro[c] <= pro[t]:
out.append(t)
else:
suffix_s.push(t)
break
#符号加入前缀栈
suffix_s.push(c)
else:
#数字直接加入结果集
out.append(c)
#清空前缀栈
while not suffix_s.is_null():
out.append(suffix_s.pop())
return ''.join(out[:-1])
#根据前缀表达式计算结果
def calculate(suffix_s):
'''根据后缀表达式求值'''
cal = {
'^': lambda x, y: x ** y,
'*': lambda x, y: x * y,
'/': lambda x, y: x / y,
'+': lambda x, y: x + y,
'-': lambda x, y: x - y
}
s = Stack()
for x in suffix_s:
if x in '^+-*/':
num2, num1 = s.pop(), s.pop()
ans = cal[x](float(num1), float(num2))
s.push(ans)
else:
s.push(x)
return s.pop()
if __name__ == '__main__':
print(calculate(solve('1-3+2*(6-1)')))
#include代码参考博客园https://www.cnblogs.com/hhh5460/p/5182081.html
(三)栈在二叉树中的应用
我们可以分别用栈实现二叉树的前序,中序,后序遍历
举例一 前序遍历(leetcode144)
给定一个二叉树,返回它的 前序 遍历。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root: return []
stack, output = [root], []
while stack:
node = stack.pop()
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
output.append(node.val)
return output
举例二 后序遍历(leetcode145)
给定一个二叉树,返回它的 后序 遍历。
#思路:按照前序遍历方法获取结果,唯一的不同是颠倒左右节点如栈顺序,
最后再将结果整体颠倒就可以得到后序遍历结果
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root: return []
stack, output = [root], []
while stack:
node = stack.pop()
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
output.append(node.val)
return output[::-1]

举例三 中序遍历(leetcode94)
给定一个二叉树,返回它的中序 遍历。参考链接
这里介绍一个更加简洁易懂且通用的方式
其核心思想如下:
如果节点status = 1,则表示已经访问,将节点的值输出
如果节点status = 0,根据前序,中序,后序要求将该节点与左右子树以此入栈
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
ans = []
stack = [(0, root)]
while stack:
status, node = stack.pop()
if not node: continue
if status == 0:
#中序遍历
stack.append((0, node.right))
stack.append((1, node))
stack.append((0, node.left))
#前序遍历
stack.append((0, node.right))
stack.append((0, node.left))
stack.append((1, node))
#后序遍历
stack.append((1, node))
stack.append((0, node.right))
stack.append((0, node.left))
else:
ans.append(node.val)
return ans
二、队列
队列(Queue)是一种先进先出(FIFO,First-In-First-Out)的线性表。队列的操作方式和堆栈类似,唯一的区别在于队列只允许新数据在后端进行添加
优先队列:
普通队列:先进先出,后进先出
优先队列:出队顺序和入队顺序无关,和优先级相关
队列的应用(leetcode529)
让我们一起来玩扫雷游戏!
给定一个代表游戏板的二维字符矩阵。 ‘M’ 代表一个未挖出的地雷,‘E’ 代表一个未挖出的空方块,‘B’ 代表没有相邻(上,下,左,右,和所有4个对角线)地雷的已挖出的空白方块,数字(‘1’ 到 ‘8’)表示有多少地雷与这块已挖出的方块相邻,‘X’ 则表示一个已挖出的地雷。
现在给出在所有未挖出的方块中(‘M’或者’E’)的下一个点击位置(行和列索引),根据以下规则,返回相应位置被点击后对应的面板:
如果一个地雷(‘M’)被挖出,游戏就结束了- 把它改为 ‘X’。
如果一个没有相邻地雷的空方块(‘E’)被挖出,修改它为(‘B’),并且所有和其相邻的方块都应该被递归地揭露。
如果一个至少与一个地雷相邻的空方块(‘E’)被挖出,修改它为数字(‘1’到’8’),表示相邻地雷的数量。
如果在此次点击中,若无更多方块可被揭露,则返回面板。
思路:根据题目要求选择一个挖地雷的位置,会出现以下几种情况:
(1)空白:递归找到其它相连的空白格以及与空白格接触的边缘方块(可以是数字也可以是雷),返回面板
(2)数字:将当前格子修改成对应数字,返回面板
(3)雷: 将当前格子修改成'X',返回面板
class Solution:
def updateBoard(self, board: List[List[str]], click: List[int]) -> List[List[str]]:
positions = [(1, 0), (-1, 0), (0, 1), (0, -1), (1, -1), (1, 1), (-1, -1), (-1, 1)]
def scan(x, y):
count = 0
for pos in positions:
tem_x, tem_y = pos[0] + x, pos[1] + y
if not(0 <= tem_x < row and 0 <= tem_y < col): continue
#判断当前格子周围雷的数量
if board[tem_x][tem_y] == 'M' or board[tem_x][tem_y] == 'X': count += 1
#如果是空白格子,将其周围未判定的格子加入队列,广度优先搜索
if not count:
for pos in positions:
if not(0 <= x+pos[0]< row and 0 <= y+pos[1] < col): continue
if board[x+pos[0]][y+pos[1]] == 'E': queue.append((x+pos[0],y+ pos[1]))
board[x][y] = str(count) if count else 'B'
#每次递归从队列头部取出一个位置
if queue:
pos = queue.pop()
scan(pos[0], pos[1])
if not board: return board
row, col = len(board), len(board[0])
queue = []
#如果踩雷,直接结束游戏
if board[click[0]][click[1]] == 'M':
board[click[0]][click[1]] = 'X'
return board
scan(click[0], click[1])
return board
778.水位上升的泳池中游泳(优先队列)
在一个 N x N 的坐标方格 grid 中,每一个方格的值 grid[i][j] 表示在位置 (i,j) 的平台高度。
现在开始下雨了。当时间为 t 时,此时雨水导致水池中任意位置的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。
你从坐标方格的左上平台 (0,0) 出发。最少耗时多久你才能到达坐标方格的右下平台 (N-1, N-1)?
class Solution {
//此题可以看作一个深度不同的模型,向模型那个倒水,
//优先队列保证水往低处流,set集合保证流过的地方不回流
public int swimInWater(int[][] grid) {
int N = grid.length;
//水可以向四个方向流
int[][] poses = {
{
0, 1}, {
0, -1}, {
-1, 0}, {
1, 0}};
//确定优先队列大小关系
PriorityQueue<Integer> pq = new PriorityQueue<Integer>((k1, k2) -> grid[k1 / N][k1 % N] - grid[k2/N][k2%N]);
Set<Integer> seen = new HashSet();
pq.offer(0); seen.add(0);
int ans = 0;
//while(true)也可以
while(!pq.isEmpty()){
int k = pq.poll();
int row = k / N, col = k % N;
ans = Math.max(ans, grid[row][col]);
if(row == N -1 && col == N -1) return ans;
for(int i = 0; i<poses.length; i++){
int temp_x = row, temp_y = col;
temp_x+=poses[i][0]; temp_y +=poses[i][1];
int ck = temp_x * N + temp_y;
if(temp_x >= 0 && temp_x < N && temp_y >= 0 && temp_y < N && !seen.contains(ck)){
pq.offer(ck);
seen.add(ck);
}
}
}
throw null;
}
}
三、堆
堆(Heap)是一个可以被看成近似完全二叉树的数组。树上的每一个结点对应数组的一个元素。除了最底层外,该树是完全充满的,而且是从左到右填充。—— 来自:《算法导论》
堆包括最大堆和最小堆:最大堆的每一个节点(除了根结点)的值不大于其父节点;最小堆的每一个节点(除了根结点)的值不小于其父节点。
堆结构的一个常见应用是建立优先队列(Priority Queue)。
import heapq
#向堆中插入元素,heapq会维护列表heap中的元素保持堆的性质
heapq.heappush(heap, item)
#heapq把列表x转换成堆
heapq.heapify(x)
#从可迭代的迭代器中返回最大的n个数,可以指定比较的key
heapq.nlargest(n, iterable[, key])
#从可迭代的迭代器中返回最小的n个数,可以指定比较的key
heapq.nsmallest(n, iterable[, key])
#从堆中删除元素,返回值是堆中最小或者最大的元素
heapq.heappop(heap)
(一)优先队列与堆排序
#最小堆,根节点一定是最小值, 优先队列必须保证每次弹出的值都是最小的。
class prioQueue:
def __init__(self, elist=[]):
self._elems = list(elist)
if elist:
self.buildheap()
#从右下方开始,每次 更新三个节点子树,将最小节点置于根节点
#从倒数第二层按层遍历
def siftdown(self, e, begin, end):
elems, i, j = self._elems, begin, begin * 2 + 1
while j < end:
if j + 1 < end and elems[j + 1] < elems[j]:
j = j + 1
if e < elems[j]:
break
elems[i] = elems[j]
i, j = j, 2 * j + 1
elems[i] = e
def buildheap(self):
end = len(self._elems)
for i in range(end//2,-1,-1):
self.siftdown(self._elems[i],i,end)
return self._elems
def heapsort(self):
ans = []
end = len(self._elems)
for i in range(end):
self.buildheap(self)
self._elems[-1], self._elems[0] = self._elems[0], self._elems[-1]
ans.append(self._elems.pop())
(二)373. 查找和最小的K对数字
给定两个以升序排列的整形数组 nums1 和 nums2, 以及一个整数 k。
定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2。
找到和最小的 k 对数字 (u1,v1), (u2,v2) … (uk,vk)。
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数:
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
思路:优先队列
class Solution:
def kSmallestPairs(self, nums1, nums2, k):
queue = []
def push(i, j):
if i < len(nums1) and j < len(nums2):
heapq.heappush(queue, [nums1[i] + nums2[j], i, j])
#它仅从矩阵左上角的第一对开始,然后根据需要从那里开始扩展。
push(0, 0)
pairs = []
while queue and len(pairs) < k:
_, i, j = heapq.heappop(queue)
pairs.append([nums1[i], nums2[j]])
#每当将一对选择为输出结果时,该行中的下一对就会添加到当前选项的优先队列中。
push(i, j + 1)
# 如果所选对是该行中的第一对,则将下一行中的第一对添加到队列中。
if j == 0:
push(i + 1, 0)
return pairs
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
int size1 = nums1.length;
int size2 = nums2.length;
List<List<Integer>> ans = new ArrayList();
//定义初始堆
for(int i = 0; i<size1; i++){
for(int j = 0; j<size2; j++){
List<Integer> temp = new ArrayList();
temp.add(nums1[i]); temp.add(nums2[j]);
ans.add(temp);
}
}
//特殊情况处理
if(k >= size1 * size2 || size1 == 0 || size2 == 0 ) return ans;
buildHeap(ans);
List<List<Integer>> res = new ArrayList();
//获取结果k
for(int j = 1; j<=k; j++){
res.add(ans.get(0));
swap(0, ans.size() - 1, ans);
ans.remove(ans.size() - 1);
heapSort(ans, 0);
}
return res;
}
---------------------------堆排序模板-------------------------
//定义交换函数 swap()
public void swap(int f, int e, List<List<Integer>> nums){
List<Integer> temp = nums.get(f);
nums.set(f, nums.get(e));
nums.set(e, temp);
}
//堆构建
public void buildHeap(List<List<Integer>> nums){
int size = nums.size();
//细节1:(size - 2)/2
for(int i = (size - 2) / 2; i>=0; i--){
heapSort(nums, i);
}
}
//堆排序
public void heapSort(List<List<Integer>> nums, int index){
List<Integer> temp = nums.get(index);
int size = nums.size();
//细节2: i = 2 * index + 1;细节三: i = 2 * i + 1
for(int i = 2 * index + 1; i<size; i = 2 * i + 1){
//细节4:子节点先比较
if(i + 1<size && compare(nums.get(i), nums.get(i+1))) i++;
if(compare(temp, nums.get(i))){
nums.set(index, nums.get(i));
index = i;
}
else break;
}
nums.set(index, temp);
}
//定义比较函数compare
public boolean compare(List<Integer> f, List<Integer> e){
int temp1 = f.get(0) + f.get(1);
int temp2 = e.get(0) + e.get(1);
if(temp1 >= temp2) return true;
else return false;
}
}
