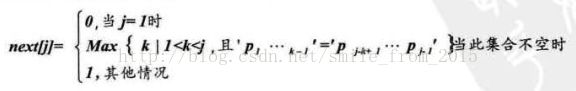串-KMP模式匹配算法

5.7 KMP 模式匹配算法

你们可以忍受朴素模式匹配算法的低效吗?也许不可以、也许无所谓。但在很多年前我们的科学家们，觉得像这种有多个0和1重复字符的字符串，却需要挨个遍历的算法是非常糟糕的事情。 于是有三位前辈，D.E.Knutb、J.H.Morris和Y.R.Pratt(其中Knuth和Pratt共同研究，Morris独立研究)发表一个模式匹配算法，可以大大避免重复遍历的情况，我们把它称之为克努特一莫里斯一普拉特算法，简称KMP算法。

5.7.1 KMP 模式匹配算法原理

为了能讲清楚KMP算法，我们不直接讲代码，那样很容易造成理解困难，还是从这个算法的研究角度来理解为什么它比朴素算法要好。

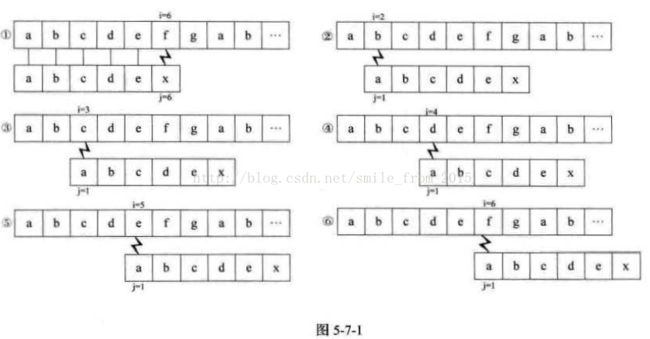
如果主串 S="abcdefgab"，其实还可以更长一些 ，我们就省略掉只保留前9位，我们要匹配的 T= "abcdex"，那么如果用前面的朴素算法的话，前5个字母，两个串完全相等，直到第6个字母，"f"与 "x" 不等，如图 5-7-1 的①所示 。

接下来，按照朴素模式匹配算法，应该是如图5-7-1的流程②③④⑤⑥。即主串S中当i=2、3 、4、5、6时，首字符与子串T的首字符均不等。

似乎这也是理所当然，原来的算法就是这样设计的。可仔细观察发现。对于要匹配的子串T来说，"abcdex" 首字母 "a" 与后面的串 "bcdex" 中任意一个字符都不相等。也就是说，既然"a"不与自己后面的子串中任何一字符相等，那么对于图5-7-1的①来说，前五位字符分别相等，意味着子串T的首字符"a"不可能与S串的第2位到第5位的字符相等。在图5-7-1中，②③④⑤的判断都是多余。

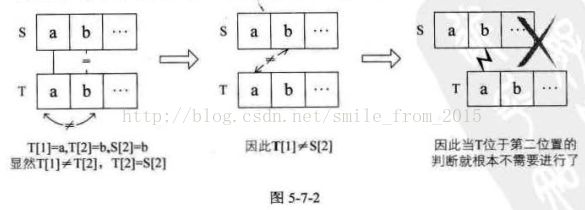
注意这里是理解KMP算法的关键。如果我们知道T串中首字符"a"与T中后面的字符均不相等(注意这是前提，如何判断后面再讲)。而T串的第二位的"b"与S串中第二位的"b"在图5-7-1 的①中已经判断是相等的，那么也就意味着。T串中首字符"a"与 S 串中的第二位"b"是不需要判断也知道它们是不可能相等了，这样固5-7-1的②这一步判断是可以省略的，如图5-7-2所示。

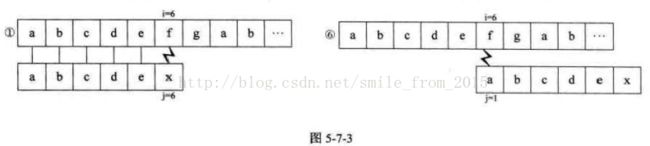
同样道理，在我们知道T串中首字符"a"与T中后面的字符均不相等的前提下，T串的"a"与S串后面的"c"、"d" 、"e" 也都可以在①之后就可以确定是不相等的，所以这个算法当中②③④⑤没有必要，只保留①⑥即可，如图5-7-3所示。

之所以保留⑥中的判断是因为在①中T[6]!=S[6]，尽管我们已经知道T[l]!=T[6]，但也不能断定T[l]一定不等于S[6]，因此需要保留⑥这一步。

有人就会问，如果T串后面也含有首字符"a" 的字符怎么办呢?

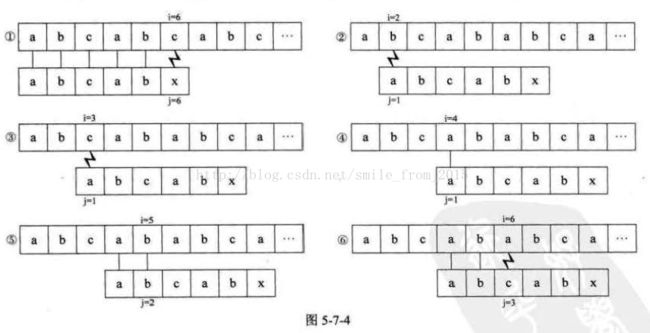
我们来看下面一个例子，假设S="abcabcabc",T="abcabx"。对于开始的判断，前5个字符完全相等，第6个字符不等，如图5-7-4的①。此时，根据刚才的经验，T的首字符"a"与T的第二位字符"b"、第三位字符"c"均不等，所以不需要做判断，图5-7-4的朴素算法步骤②③都是多余。

因为T的首位"a"与T第四位的"a"相等，第二位的"b"与第五位的"b"相等。而在①时，第四位的"a"与第五位的"b" 已经与主串S中的相应位置比较过了，是相等的，因此可以断定，T的首字符"a"、第二位的字符"b"与S 的第四位字符和第五位字符也不需要比较了，肯定也是相等的一一之前比较过了，还判断什么。所以④⑤这两个比较得出字符相等的步骤也可以省略 。

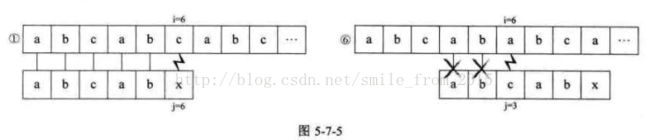
也就是说，对于在子串中有与首字符相等的字符，也是可以省略一部分不必要的判断步骤。如图5-7-5所示 ，省略掉下图的T串前两位"a"与"b"同S串中的4、5位置字符匹配操作。

对比这两个例子，我们会发现在①时，我们的i值，也就是主串当前位置的下标是6，②③④⑤，i值是2、3 、4、5，到了⑥，i值才又回到了6。即我们在朴素的模式匹配算法中，主串的i值是不断地回溯来完成的。而我们的分析发现，这种回溯其实是可以不需要的一一正所谓好马不吃回头萃，我们的KMP模式匹配算法就是为了让这没必要的回溯不发生。

既然i值不回溯，也就是不可以变小，那么要考虑的变化就是j值了。通过观察也可发现，我们屡屡提到了T串的首字符与自身后面字符的比较，发现如果有相等字符，j值的变化就会不相同。也就是说，这个j值的变化与主串其实没什么关系，关键就取决于T串的结构中是否有重复的问题。

比如图5-7-3中，由于 T="abcdex"，当中没有任何重复的字符，所以j就由6变成了1。而图5-7-4中，由于 T="abcabx"，前缀的"ab"与最后"x"之前串的后缀"ab"是相等的。因此j就由6变成了"3" 因此，我们可以得出规律，j值的多少取决于当前字符之前的串的前后缀的相似度。

我仍把T串各个位置的j值的变化定义为一个数组next，那么next的长度就是T串的长度。于是我们可以得到下面的函数定义:

5.7.2 next数组值推导

具体如何推导出一个串的next数组值呢，我们来看一些例子 。

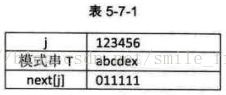
1 . T="abcdex" (如表5-7-1所示)

1 ) 当 j=1 时，next[1]=0;

2 ) 当 j =2 时，j 由 1 到 j -1 就只有字符"a"，属于其他情况next[2]=1;

3 ) 当 j =3 时，j 由 1 到 j- 1 串是"ab"，显然"a"与"b"不相等，属其他情况，next[3]=1;

4 )以后同理，所以最终此T串的 next[j]为011111。

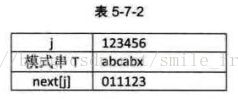
2. T="abcabx"(如表5-7-2所示)

1 ) 当 j=1 时 ， next[1]=0;

2 ) 当 j=2 时，同上例说明， next[2]=1;

3 ) 当 j=3 时，同上，next[3]=1;

4 ) 当 j=4 时，同上，next[4]=1;

5 ) 当 j=5 时，此时j由1到j-1的串是" a bc a "，前缀字符"a"与后缀字符"a"相等(前缀用下划线表示，后缀用斜体表示)，因此可推算出k值为2(由'pl……p(k-1)=p(j-k+1)……p(j-1)'，得到p1=p4)因此next[5]=2;

6 ) 当 j=6 时， j 由1到j - l的串是"abcab" ，由于前缀字符 "ab" 与后缀 "ab"相等，所以 next[6]=3。

我们可以根据经验得到如果前后缀一个字符相等，k值是2，两个字符k值是3 ，n个相等 k 值就是 n+1。

3. T="ababaaaba" (如表 5-7-3 所示)

1 ) 当 j=1 时， next[1]=0;

2 ) 当 j=2 时，同上next[2]=1;

3 ) 当 j=3 肘，同上next[3]=1;

4 ) 当 j=4 时， j 由 1 到 j-1 的串是" a b a "，前缀字符"a"与后缀字符"a"相等,next[4]=2;

5 ) 当 j=5 时， j 由 1 到 j-1 的串是" ab ab "，由于前缀字符"ab"与后缀"ab"相等，所以next[5]=3;

6 ) 当 j=6 时， j 由 1 到 j-1 的串是" ab a ba "，由于前缀字符"aba"与后缀"aba"相等，所以next[6]=4;

7 ) 当 j=7 时， j 由 1 到 j-1 的串是" a baba a "，由于前缀字符"ab"与后缀"aa"并不相等，只有"a"相等，所以next[7]=2;

8 ) 当 j=8 时， j 由 1 到 j-1 的串是" a babaa a "，只有"a"相等，所以next[8]=2;

9 ) 当 j=9 时， j 由 1 到 j-1 的串是" ab abaa ab "，由于前缀字符"ab"与后缀"ab"相等，所以next[9]=3。

4 . T="aaaaaaaab"(如表5-7-4所示)

1 ) 当 j = 1 时， next[l]=0;

2 ) 当 j=2 时，同上 next[2]=1;

3 ) 当 j=3 时，j 由 1 到 j - 1 的串是" a a ",前缀字符"a"与后缀字符"a"相等，next[3]=2;

4 ）当 j=4 时，j 由 1 到 j - 1 的串是" a a a "，由于前缀字符"aa"与后缀"aa"相等，所以next[4]=3;

5 ) ......

6 ) 当 j=9 时, j 由 1 到 j-l 的串是" a aaaaaa a "，由于前缀字符"aaaaaaa"与后缀"aaaaaaa" 相等，所以next[9]=8。

5.7.3 KMP 模式匹配算法实现

说了这么多，我们可以来看看Java代码了。

/**通过计算返回子串t的next数组*/
static int[] get_next(String[] t){
	int i,j;
	i = 1;
	j = 0;
	int[] next = new int[t.length];
	next[1] = 0;
	while(	i < Integer.parseInt(t[0])){
		if(j == 0 || t[i] == t[j]){/*t[i]表示后缀的单个字符 ,t[j]表示前缀的单个字符 。*/
			++i;
			++j;
			next[i] = j;
		}else
			j = next[j];//若字符不相同，则 j值回溯
	}
	next = Arrays.copyOfRange(next, 1, next.length);
	return next;
}

这段代码的目的就是为了计算出当前要匹配的串T的next数组。

/**
 * t为非空串 。 若主串 s中第 pos个字符之后存在与 t相等的子串.
 * 则返回第一个这样的子串在s中的位置，否则返回-1
 * 1<=pos<=s.length()
 * @param s
 * @param t
 * @param pos
 * @return
 */
static int index_KMP(String[] s,String[] t,int pos){
	int i = pos;/*用于主串s当前位置下标值，若pos不为1，则从pos位置开始匹配*/
	int j = 1;/*j用于子串t中当前位置下标*/
	int[] next = new int[255];/*定义next数组*/
	next = get_next(t);//对串t进行分析，得到next数组
	/*若i小于s的长度且j小于t的长度，循环继续*/
	while(i <= Integer.parseInt(s[0]) && j <= Integer.parseInt(t[0])){
		if(j == 0 || s[i].equals(t[j])){
			++i;
			++j;
		}else{//j回溯
			j = next[j-1];//j退回到合适的位置，i值不变  （加粗部分）
		}
	}
	if(j > Integer.parseInt(t[0])){
		return i - Integer.parseInt(t[0]);
	}else
		return -1;
}

加粗的为相对于朴素匹配算法增加的代码，改动不算大，关键就是去掉了i值回溯的部分。对于get_next函数来说，若T的长度为m，因只涉及到简单的单循环，其时间复杂度为O(m),而由于i值得不回溯，使得index_KMP算法效率得到了提高，while循环的时间复杂度为O(n)。因此，整个算法的时间复杂度为O(m+n)。相较于朴素模式匹配算法的O((n-m+1)*m)来说，是要更好一些。

这里也需要强调，KMP算法仅当模式与主串之间存在许多"部分匹配"的情况下才体现出它的优势，否则两者差异并不明显。

5.7.4 KMP模式匹配算法改进

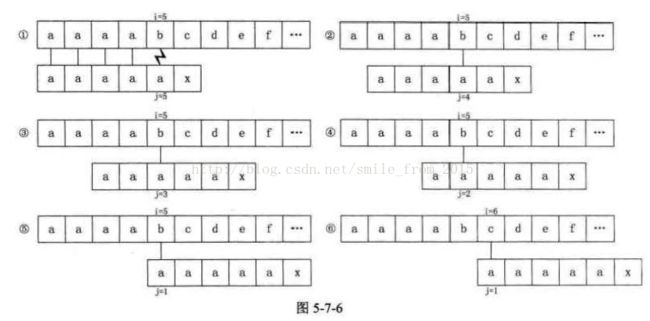
后来有人发现，KMP还是有缺陷的。比如，如果我们的主串S="aaaabcde"，子串T="aaaax"，其next数组值分别为012345，在开始时，当 i=5、j=5时，我们发现"b"与"a"不相等，如图5-7-6的①，因此j=next[5]=4，如图中的②，此时"b"与第4位置的"a"依然不等，j=next[4}=3。如图中的③，接着依次是④⑤，直到 j=next[l]=0时，根据算法，此时i++、j++，得到i=6、j=l如图中的⑥。

我们发现，当中的②③④⑤步骤，其实是多余的判断。由于T串的第二、三、四、五位置的字符都与首位的 "a" 相等，那么可以用首位 next[l]的值去取代与它相等的字符后续next[j]的值，这是个很好的办法。因此我们对求next函数进行了改良。

假设取代的数组为nextval，增加了加粗部分，Java代码如下:

/**求模式串T的next函数值并存入数组nextVal*/
static int[] get_nextVal(String[] t){
	int i,j;
	i = 1;
	j = 0;
	int[] nextVal = new int[t.length];
	nextVal[1] = 0;
	while(	i < Integer.parseInt(t[0])){//t[0]存放数组的长度
		if(j == 0 || t[i] == t[j]){/*t[i]表示后缀的单个字符 ,t[j]表示前缀的单个字符 。*/
			++i;
			++j;
			if(t[i] != t[j])/*若当前字符与前缀字符不同，则当前的j为nextVal在i位置的值*/
				nextVal[i] = j;
			else
				nextVal[i] = nextVal[j];//如果与前缀字符相同，则将前缀字符的nextVal值赋值给nextVal在i位置的值*
		}else
			j = nextVal[j];//若字符不相同，则 j值回溯
	}
	nextVal = Arrays.copyOfRange(nextVal, 1, nextVal.length);
	return nextVal;
}

5.7.5 nextval数组值推导

改良后，我们之前的例子nextval值就与next值不完全相同了。比如 :

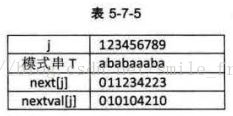
1. T="ababaaaba" (如表5-7-5所示)

先算出next数组的值分别为011234223，然后再分别判断。

1 ) 当j=1时，nextval[1] =0;

2 ) 当j=2时，因第二位字符"b"的next值是1，而第一位就是"a"，它们不相等，所以nextval[2]=next[2]=1 ，维持原值。

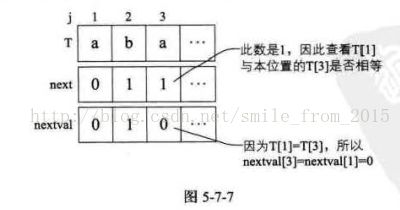
3 ) 当j=3时，因为第三位字符"a"的 next 值为1，所以与第一位的"a"比较得知它们相等，所以nextval[3]=nextval[l]=0;如图5-7-7所示。

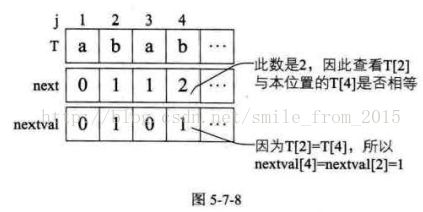
4 ) 当 j=4 时，第四位的字符"b"next值为2 ，所以与第二位的"b" 相比较得到结果是相等，因此nextval[4]=nextval[2]=1;如图5-7-8所示。

5 ) 当j=5时，next值为3，第五个字符"a"与第三个字符"a"相等，因此nextval[5]=nextva1[3]=0;

6 ) 当j=6时，next值为4，第六个字符"a"与第四个字符"b"不相等，因此nextval[6]=4;

7 ) 当j=7时，next值为2, 第七个字符"a"与第二个字符"b"不相等，因此nextva1[7] =2;

8 ) 当j=8时，next值为2，第八个字符"b"与第二个字符"b"相等，因此nextva1[8]=nextva1[2]=1;

9 ) 当j=9时，next值为3，第九个字符"a"与第三个字符"a"相等，因此nextval[9]=nextval[3}=l。

2. T="aaaaaaaab" (如表5-7-6）

先算出next数组的值分别为012345678，然后再分别判断。

1 ) 当 j=1 时，nextval[l]=0;

2 ) 当 j=2 时，next 值为 1 ，第二个字符与第一个字符相等，所以 nextval[2] =nextva1[l]=0;

3 ) 同样的道理，其后都为 0……;

4 ）当 j=9 时 ，next值为8，第九个字符 "b"与第八个字符"a" 不相等，所以nextva1[9]=8。

总结改进过的KMP算法，它是在计算出next值的同时，如果a位字符与它next值指向的b位字符相等，则该a位的nextval就指向b位的nextval值，如果不等，则该a位的nextval值就是它自己a位的next的值。

5.8 总结回顾

这一章节我们主重点讲了"串"这样的数据结构，串 (string) 是由零个或多个字符组成的有限序列，又名叫字符串。本质上，它是一种线性表的扩展，但相对于线性表关注一个个元素来说，我们对串这种结构更多的是关注它子串的应用问题，如查找、替换等操作。现在的高级语言都有针对串的函数可以调用。我们在使用这些函数的时候，同时也应该要理解它当中的原理，以便于在碰到复杂的问题时，可以更加灵活的使用，比如KMP 模式匹配算法的学习，就是更有效地去理解index函数当中的实现细节。多用心一点，说不定有一天，可以有以你的名字命名的算法流传于后世。

引用《大话数据结构》作者：程杰