2019-2020 ACM-ICPC Brazil Subregional Programming Contest 题解

题目链接:http://codeforces.com/gym/102346

 

A. Artwork

将相交的圆用并查集合并，最后查询一下是否有一个或者两个在一个并查集里面的圆形成这样的一个封闭

#include 
#define x first
#define y second
#define mid (l+r>>1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
using namespace std;
typedef long long int ll;
typedef pair pa; 
const int mx = 1e5 + 10;
struct circle{
	ll x,y,r;
}c[mx];
	int n,m,k;
int p[mx];
int find(int x){
	return p[x]==x?x:p[x] = find(p[x]);
}
ll power(ll x){
	return x*x;
}
bool judge(circle a,circle b){
	return power(a.x-b.x)+power(a.y-b.y) <= a.r*a.r+b.r*b.r+2*a.r*b.r;	
}
bool check(circle a,circle b){
	if(a.x-a.r>0&&a.y+a.r0)
		return false;
	return true;
}
int main()
{	
	scanf("%d%d%d",&n,&m,&k);
	for(int i = 1; i <= k; i++)
		scanf("%lld%lld%lld",&c[i].x,&c[i].y,&c[i].r),p[i] = i;
	for(int i = 1; i <= k; i++)
		for(int j = i+1; j <= k; j++)
			if(judge(c[i],c[j])){
				int x = find(i);
				int y = find(j);
				if(x!=y)
					p[x] = y;
			}
			
	for(int i = 1; i <= k; i++)
		find(i);
	bool ok = true;
	for(int i = 1; i <= k; i++)
		for(int j = 1; j <= k; j++){
			if(check(c[i],c[j])&&p[i]==p[j])
				ok = false;
		}
	ok?puts("S"):puts("N");
	return 0;
} 

B. Buffoon

水题

C.Crossings With Danger

未做

D.Denouncing Mafia

实际上是一个树形DP,还有就是链的个数最多就是叶子节点个数，所以只要确定每个点是属于哪个叶子形成的链就好了，然后最后排个序输出前k大

#include 
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
using namespace std;
typedef long long ll;
const int mx = 1e5 + 10;
int n,m,w[mx];
vector  g[mx]; 
priority_queue  q;
void dfs_val (int u) {
	int son = 0;
	w[u] = 1;
	for (int v:g[u]) {
		dfs_val(v);
		if (w[v] > w[son])
			son = v;
	}
	for (int v:g[u]) {
		if (v != son)
			q.push(w[v]);
	}
	w[u] += w[son];
}
int main()
{
	scanf("%d%d",&n,&m);
	int u;
	for (int i=2;i<=n;i++) {
		scanf("%d",&u);
		g[u].push_back(i);
	}
	dfs_val(1);
	q.push(w[1]);
	int ans = 0;
	while (m-- && q.size()) {
		ans += q.top();
		q.pop();
	}
	printf("%d\n",ans);
	return 0;
}

E.Exhibition of Clownfish

未做

F.Forests in Danger

二分答案，然后就是求每个矩形与目标矩形的矩形交，然后求这些矩形交的面积并，这就是常见模板了，然后最后看下面积有没有是目标矩形的P%。

#include 
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
using namespace std;
typedef long long ll;
const int mx = 2e4 + 10;
int n,P;
int b[mx];
int x1,x2,y1,y2;
struct node {
	int x1,y1;
	int x2,y2;
}s[mx];

struct seg {
	int l,r;
	int h,d;
	bool operator < (seg A) const {
		return h < A.h;
	}
}a[mx];

int cnt[mx<<2],sum[mx<<2];

void push_up(int l, int r, int rt) {
    if(cnt[rt]) sum[rt] = b[r + 1] - b[l];
    else if(l == r) sum[rt] = 0; //leaves have no sons
    else sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
 
void update(int l, int r, int rt, int L, int R, int v) {
    if(L <= l && r <= R) {
        cnt[rt] += v;
        push_up(l, r, rt);
        return;
    }
    int mid = l + r >> 1;
    if(L <= mid) update(lson, L, R, v);
    if(R > mid) update(rson, L, R, v);
    push_up(l, r, rt);
}

bool check(int mid) {
	static ll area = 1ll*(x2-x1)*(y2-y1);
	int siz = 0, is = 0;
	int X1,X2,Y1,Y2;
	memset(sum,0,sizeof(sum));
	memset(cnt,0,sizeof(cnt));
	for (int i=1;i<=n;i++) {
		X1 = s[i].x1 - mid;
		X2 = s[i].x2 + mid;
		Y1 = s[i].y1 - mid;
		Y2 = s[i].y2 + mid;
		int lx = max(X1,x1);
		int rx = min(X2,x2);
		int ly = max(Y1,y1);
		int ry = min(Y2,y2);
		if (lx > rx || ly > ry) continue;
		b[++siz] = lx;
		a[siz] = {lx,rx,ly,1};
		b[++siz] = rx;
		a[siz] = {lx,rx,ry,-1};
	}
	sort(b+1,b+siz+1);sort(a+1,a+siz+1);
	is = unique(b+1,b+siz+1) - b;
	ll ans = 0;
	for (int i=1;i<=siz;i++) {
		int L = lower_bound(b+1,b+is,a[i].l) - b;
		int R = lower_bound(b+1,b+is,a[i].r) - b - 1;
		
        update(1,is-1,1,L,R,a[i].d);//扫描线段时更新底边长度和底边相差个数
        ans += 1ll*sum[1]*(a[i+1].h-a[i].h);//新增加面积
	}
	return ans * 100 / area >= P;
} 
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++) {
		scanf("%d%d%d%d",&s[i].x1,&s[i].y1,&s[i].x2,&s[i].y2); 
	}
	scanf("%d",&P);
	scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
	int l = 1,r = 1e6;
	while (l < r) {
		int mid = l+r>>1;
		if (check(mid))
			r = mid;
		else 
			l = mid + 1;
	}
	printf("%d\n",l);
	return 0;
}

G.Getting Confidence

把每个数变成一个指数的幂，然后乘法就变成了加法log(a)+log(b) = log(a*b),之后就是最大权二分匹配了，直接上板子就好了

#include
#define inf 0x3f3f3f3f
using namespace std;
const int mx = 1e2 + 10;
const double eps = 1e-8;
typedef long long ll;
int n,m;
double w[mx][mx],lx[mx],ly[mx];
double slack[mx];
int cp[mx];
bool visx[mx],visy[mx];
bool find(int x)
{
	visx[x] = 1;
	for(int i=1;i<=n;i++){
		if(!visy[i]){
			double val = lx[x] + ly[i] - w[x][i];
			if(fabs(val)

H.Hour for a Run

水题

I.Interplanetary

未做

J,Jar of Water Game

照着题目模拟就好了

#include
using namespace std;
const int inf = 0x3f3f3f3f;

struct People {
	int a[7];
	int k;
} p[20];
map mp;
int n, m;

void handle() {
	mp['A'] = 1;
	mp['D'] = 10;
	mp['Q'] = 11;
	mp['J'] = 12;
	mp['K'] = 13;
	for(int i=2; i<=9; i++) {
		mp[i+'0'] = i;
	}	
}

int get(People &p) {
	if(p.k) {
		if(p.k == 1)	p.k++;
		else return inf; 
	}
	int c = 5;
	if(p.k)	c--;
	int cnt[20] = {0};
	for(int i=1; i<=c; i++) {
		cnt[p.a[i]]++;
	}
	int mn = 10;
	for(int i=1; i<=c; i++) {
		mn = min(mn, cnt[p.a[i]]);
	}
	int ans = 20;
	for(int i=1; i<=c; i++) {
		if(cnt[p.a[i]] == mn)	ans = min(ans, p.a[i]);
	}
	return ans;
}

void give(People &p, int pai) {
	if(pai == inf) {
		p.k = 1;
		return ;
	} else {
		int c = 5;
		if(p.k)	c--;
		p.a[c] = pai;
	}
}

void del(People &p, int pai) {
	if(pai == inf) {
		p.k = 0;
		return ;
	}
	int c = 5;
	if(p.k)	c--;
	for(int i=1; i<=c; i++) {
		if(p.a[i] == pai) {
			swap(p.a[i], p.a[c]);
			p.a[c] = 0;
			break;
		}
	}
}

bool ok(People p) {
	if(p.k)	return false;
	if(p.a[1] != p.a[2])	return false;	
	if(p.a[1] != p.a[3])	return false;	
	if(p.a[1] != p.a[4])	return false;	
	return true;
}

int main() {
	handle();
	scanf("%d%d", &n, &m);
	for(int i=1; i<=n; i++) {
		char s[10];
		scanf("%s", s+1);
		for(int j=1; j<=4; j++) {
			p[i].a[j] = mp[s[j]];
		}
		p[i].k = 0;
	}
	p[m].k = 1;

	for(int i=1; i<=n; i++) {
		if(i == m)	continue;
		if(ok(p[i])) {
			printf("%d\n", i);
			return 0;
		}
	}

	int now = m, nex;
	while(1) {
		nex = now+1;
		if(nex == n+1)	nex = 1;
		int pai = get(p[now]);
		del(p[now], pai);
		give(p[nex], pai);
		if(ok(p[now])) {
			printf("%d\n", now);
			break;
		}
		now = nex;
	}
	return 0;
}

K.Keep Calm and Sell Balloons

先上公式:

              f(n) = 2*f(n-1) + 4*f(n-2) + 2^(n-1)  f(1) = 1, f(0) = 0

              t(n) =  2*t(n-1) + 8*f(n-2)  t(2) = t(1) = 0

              ans(n) = 4*f(n) + 2*t(n)

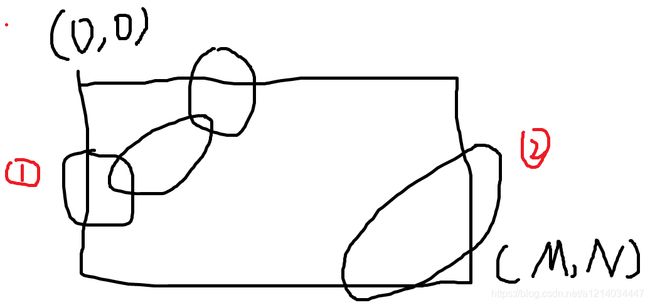
t(n)和f(n)都可以用一个4阶矩阵求出。其中f(n)起点在边界的方案数，因为起点在边界的有4种,所以乘以4，t(n)表示以非边界点为起点的方案数，因为非边界点每一列可以有上下两种选择，所以乘以2。

上图n列的边界点1和2，设g(n)表示从1点出发到2点的方案数，很容易知道g(n)=2*g(n-1)，所以g(n) = 2^(n-1)

那么f(n)也就是从1点出发的所有方案数，也就是上面的式子，4*f(n-2)的由来是这样的

这是两种前面4格的走法，所以要再乘以2，2*f(n-1)也就是先从1走到2然后再走剩下n-1列

然后t(n)就是画红线那么些非边界格子

很容易想到在中间开始的点，格子被分成了两个部分，一个部分肯定要是g(i)的形式，另一部分是f(n-1-i)的形式

由于g(n)的形式，t(n)可以直接有2*t(n-1)得到，但还缺少了f(n-2)和g(1)的组合，所以要再加上8*f(n-2)，至于这些系数大家直接去想想看为什么吧，也不难。

#include
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
const int mx = 1e6+5;
struct mat{
	ll x[4][4];
	friend mat operator*(mat &a,mat &b){
		mat c;
		for(int i = 0; i < 4; i++)
			for(int j = 0; j < 4; j++){
				c.x[i][j] = 0;
				for(int k = 0; k < 4; k++)
					c.x[i][j] = (c.x[i][j]+a.x[i][k]*b.x[k][j]%mod)%mod;
			}
		return c;
	}
};
mat x = {2,4,0,2,1,0,0,0,0,8,2,0,0,0,0,2};
mat modexp(mat x,mat ans,ll n){
	while(n){
		if(n&1) ans = x*ans;
		x = x*x;
		n /= 2;
	}
	return ans;
}
int main(){
	int n;
	scanf("%d",&n);
	mat ans;
	if(n==1){
		puts("2");
		return 0;	
	}
	ans.x[0][0] = 6;
	ans.x[1][0] = 1;
	ans.x[2][0] = 0;
	ans.x[3][0] = 2;
	ans = modexp(x,ans,n-2);
	ll sum = 4*ans.x[0][0]%mod+2*ans.x[2][0]%mod;
	sum %= mod;
	printf("%lld\n",sum);
	return 0;
}

L.Less Coin Tosses

根据lucas定理可知，答案是二进制位上1的个数的次方

#include 
#define x first
#define y second
#define mid (l+r>>1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
using namespace std;
typedef long long int ll;
typedef pair pa; 
const int mx = 1e5 + 10;
int main()
{
	ll n;
	scanf("%lld",&n);
	ll ans = 1;
	while(n){
		if(n&1) ans = ans*2;
		n /= 2;
	}
	printf("%lld\n",ans);
	return 0;
} 

M.Maratona Brasileira de Popcorn

二分即可

#include 
using namespace std;
typedef long long int ll;
const int mx = 1e5 + 10;
ll a[mx];
int n,c,t;
bool check(ll x){
	int sum = c;
	ll col = 0;
	for(int i = 1; i <= n; i++){
		if(col