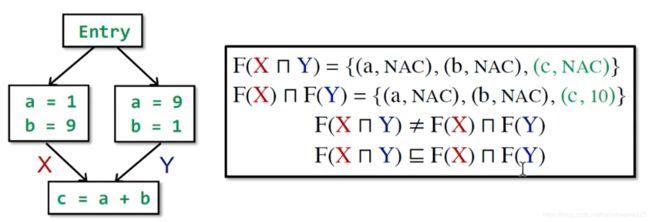软件分析——数据流分析2
数据流分析的理论部分（foundation）
这一部分李越老师用了两课时（第五课
，第六课
），讲的很仔细，将一些比较抽象的概念也解释的很清楚，收获很多，顺便做了笔记和一点从自己角度的理解，将比窘上传，方便之后需要时再看，也欢迎大家阅读以及批评指正。
1. 迭代算法（iterative algorithm）
主要由上节课的三个算法引出迭代算法，从另一个角度来分析算法，从而更深刻的理解该算法
常见的迭代算法会产生一个数据流分析的解（eg：可达定义的最后一次迭代的结果，就是数据流分析的一个解）
-
从另一个角度去看迭代算法
-
理论方面
理论1：给定一个CFG有k个点（个人理解为有k个程序点，或者就是BB），迭代算法会在每次迭代的时候，更新每个程序点的OUT[n]
理论2：设数据流分析中解的值域为V，那么可以定义一个k-元组： ( O U T [ n 1 ] , O U T [ n 2 ] , . . . O U T [ n k ] ) (OUT[n_1],OUT[n_2],...OUT[n_k]) (OUT[n1],OUT[n2],...OUT[nk])
它们是集合 ( V 1 × V 2 × . . . × V k ) (V_1 \times V_2 \times... \times V_k) (V1×V2×...×Vk)中的一个元素（该集合其实就是幂集），可以写为 V k V^k Vk，代表每次迭代后，整体的值
理论3：每一次迭代都可以看成一个 V k V^k Vk映射到一个新的 V k V^k Vk，通过转换函数和控制流来实现映射，可以将其抽象为一个函数： F : V k → V k F:V^k \to V^k F:Vk→Vk
理论4：算法不断迭代，直到相邻两次迭代的k-元组的值一样，算法就结束了
-
举例
这边可以引出：不动点的概念 x i = f ( x i ) x_i = f(x_i) xi=f(xi)，就是不动点
-
-
根据上面的角度，我们提出问题:
- 算法是否能保证一定停止或者就是抵达一个不动点（到不动点，根据算法限制的条件，就是停止的了），或者算法总是能得出一个解？
- 如果算法可终止，是否只有一个解/一个不动点？如果有多个的话，我们的解是最优的吗？
- 什么时候算法能到达一个不动点，或者什么时候我们能得到一个解？
2. 偏序（partial order）
是数学概念
定义：给定一个偏序集poset，是一组 ( P , ⊑ ) (P,\sqsubseteq) (P,⊑)，其中 ⊑ \sqsubseteq ⊑是一个定义在P上的二元关系，它必须要满足如下性质才能算是偏序关系：
- ∀ x ∈ P , x ⊑ x \forall x \in P,x \sqsubseteq x ∀x∈P,x⊑x：满足自反性，自己和自己是满足偏序关系的
- ∀ x , y ∈ P , x ⊑ y ∧ y ⊑ x ⇒ x = y \forall x,y \in P, x\sqsubseteq y\land y\sqsubseteq x \Rightarrow x = y ∀x,y∈P,x⊑y∧y⊑x⇒x=y：对称性，x是y的偏序，y是x的偏序，则x = y
- ∀ x , y ∈ P , x ⊑ y ∧ y ⊑ z ⇒ x ⊑ z \forall x,y\in P,x\sqsubseteq y \land y\sqsubseteq z\Rightarrow x\sqsubseteq z ∀x,y∈P,x⊑y∧y⊑z⇒x⊑z：传递性
举例：
三个条件依次判断：
（1）自反： 1 ≤ 1 , 2 ≤ 2 1\le 1,2\le 2 1≤1,2≤2，满足
（2）反对称： x ≤ y , y ≤ x x \le y,y \le x x≤y,y≤x，在整数中，很显然满足
（3）传递： 1 ≤ 2 , 2 ≤ 3 ⇒ 1 ≤ 3 1 \le 2,2\le 3 \Rightarrow 1\le 3 1≤2,2≤3⇒1≤3，满足
所以该关系满足偏序
如果条件改为 ⊑ 代 表 < \sqsubseteq 代表 < ⊑代表<，那么显然不满足
举例2：
三个条件依次判断
（1）自反：自己就是自己的子集，满足
（2）反对称：满足
（3）传递：in - sing，sing-singing => in - singing
该关系满足偏序
可以发现一个结论：偏序意味着集合中的两个元素可以不相互比较，即集合中不是任意两个元素都必须满足偏序关系的
举例3：也是满足偏序的
3. 上界和下界（upper and lower bounds）
给定一个偏序集 ( P , ⊑ ) (P,\sqsubseteq) (P,⊑)，并且子集S满足 S ⊆ P S \subseteq P S⊆P
上界：如果 ∀ x ∈ S , x ⊑ u , 其 中 u ∈ P \forall x \in S, x\sqsubseteq u, 其中u\in P ∀x∈S,x⊑u,其中u∈P，那么u就是子集P的上界（就是子集S中的所有元素均满足 x ⊑ u x \sqsubseteq u x⊑u）
下界：如果 ∀ x ∈ S , l ⊑ x , 其 中 l ∈ P \forall x \in S, l\sqsubseteq x, 其中l\in P ∀x∈S,l⊑x,其中l∈P，那么l就是子集P的下界（就是子集S中的所有元素均满足 l ⊑ x l\sqsubseteq x l⊑x）
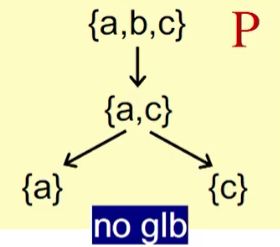
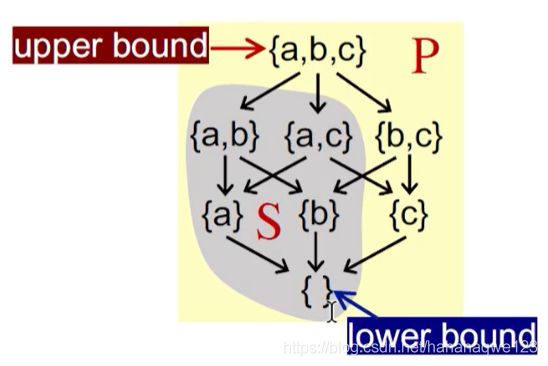
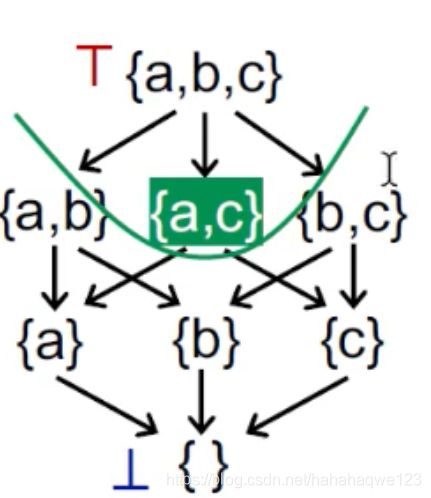
举例：对于如下的子集S，{a, b, c}就是S的上界；{ }就是S的下界
最小上界：least upper bound（lub 或者称为join），用 ⊔ S \sqcup S ⊔S表示
定义为：对于子集S的任何一个上界u，均有 ⊔ S ⊑ u \sqcup S \sqsubseteq u ⊔S⊑u
最大下界：greatest lower bound（glb 或者称为meet），用 ⊓ S \sqcap S ⊓S
定义为：对于子集S的任何一个下界l，均有 l ⊑ ⊓ S l \sqsubseteq \sqcap S l⊑⊓S
举例：
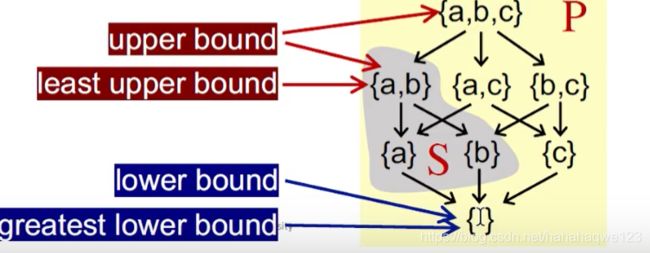
通常：如果S只包含两个元素a、b（S = {a, b}）那么上界可以表示为 a ⊔ b a \sqcup b a⊔b，下界可以表示为 a ⊓ b a \sqcap b a⊓b
一些性质：
-
不是每个偏序集都有lub/glb
对于P的子集{a}{c}来说，它没有glb，因为他们两个如果有glb的话应该是 { }，但是在P中不存在 { } -
如果存在lub/glb，那么它将是唯一的
证明：
（根据反对称性即可证明）
4. lattice（格子） ，semilattice（半格），complete lattice（完全lattice）and product lattice（lattice积）
是基于偏序和glb、lub得出的结论
-
lattice定义：给定一个偏序集 ( P , ⊑ ) (P,\sqsubseteq) (P,⊑)， ∀ a , b ∈ P \forall a,b \in P ∀a,b∈P，如果存在 a ⊔ b a\sqcup b a⊔b和 a ⊓ b a \sqcap b a⊓b，那么就称该偏序集为lattice
通俗来讲偏序集中的任意两个元素构成的集合均存在最小上界和最大下界，那么该偏序集就是lattice
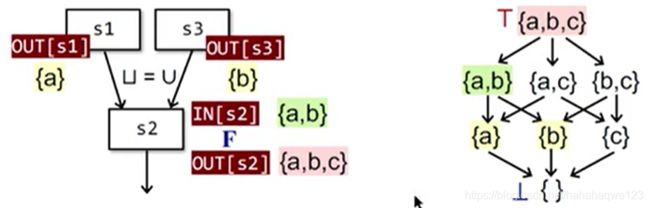
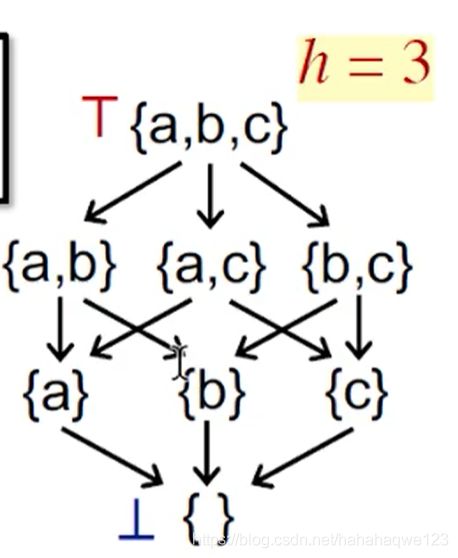
举例1：
任意两个元素之间一定存在一个上界（最大值）和一个下界（最小值），所以是lattice举例2:
pin和sin之间没有上界，所以不存在最小上界；但是有下界，且有最小下界举例3：
是lattice，并且幂集是一个经典的lattice例子 -
semilattice（半格）
给定一个偏序集 ( P , ⊑ ) (P,\sqsubseteq) (P,⊑)， ∀ a , b ∈ P \forall a,b\in P ∀a,b∈P，当且仅当 a ⊔ b a\sqcup b a⊔b存在，那么该偏序集被称为join semilattice
当且仅当 a ⊓ b a \sqcap b a⊓b存在，那么该偏序集被称为meet semilattice
通俗讲，就是只满足一半，要么只有最小上界、要么只有最大下界
-
complete lattice（完全格子）
给定一个lattice ( P , ⊑ ) (P,\sqsubseteq) (P,⊑)，对于任意P的子集S，如果 ⊔ S \sqcup S ⊔S和 ⊓ S \sqcap S ⊓S存在，那么该lattice就是完全lattice
eg1：
反例：包含所有正整数的集合，那么它没有上界eg2：
幂集是complete lattice一些符号：top、bottom
规律：任何有限的lattice是完全的lattice反之不成立（完全lattice就是有限lattice），反例：[0, 1]，在0~1之间的小数是无穷的，但是有上界、下界
-
lattice积
给定一组lattice， L 1 = ( P 1 , ⊑ 1 ) , L 2 = ( P 2 , ⊑ 2 ) , . . . , L n = ( P n , ⊑ n ) L_1=(P_1,\sqsubseteq_1),L_2 = (P_2,\sqsubseteq_2),...,L_n = (P_n,\sqsubseteq_n) L1=(P1,⊑1),L2=(P2,⊑2),...,Ln=(Pn,⊑n)都有最小上界 ⊔ i \sqcup_i ⊔i和最大下界 ⊓ i \sqcap_i ⊓i，那么可以定义lattice积： L n = ( P , ⊑ ) L^n = (P,\sqsubseteq) Ln=(P,⊑)为如下：
- P = P 1 × . . . × P n P = P_1 \times...\times P_n P=P1×...×Pn
- ( x 1 , . . . . x n ) ⊑ ( y 1 . . . . y n ) ⟺ (x_1,....x_n) \sqsubseteq (y_1....y_n) \Longleftrightarrow (x1,....xn)⊑(y1....yn)⟺ ( x 1 ⊑ y 1 ) ∧ . . . ∧ ( x n ⊑ y n ) (x_1\sqsubseteq y_1) \land...\land(x_n\sqsubseteq y_n) (x1⊑y1)∧...∧(xn⊑yn)
- ( x 1 . . . . x n ) ⊔ ( y 1 . . . y n ) (x_1....x_n)\sqcup(y_1...y_n) (x1....xn)⊔(y1...yn) = ( x 1 ⊔ 1 y 1 , . . . , x n ⊔ n y n ) (x_1\sqcup_1 y_1,...,x_n\sqcup_n y_n) (x1⊔1y1,...,xn⊔nyn)
- ( x 1 . . . . x n ) ⊓ ( y 1 . . . y n ) (x_1....x_n)\sqcap(y_1...y_n) (x1....xn)⊓(y1...yn) = ( x 1 ⊓ 1 y 1 , . . . , x n ⊓ n y n ) (x_1\sqcap_1 y_1,...,x_n\sqcap_n y_n) (x1⊓1y1,...,xn⊓nyn)
性质：lattice积也是lattice；
如果lattice积是一系列 完全lattice 的积，那么lattice积也是 complete的
5. 通过lattice来构建数据流分析框架
数据流分析框架可以变成 ( D , L , F ) (D,L,F) (D,L,F)：
- D：代表数据流的方向：前向or反向
- L：就是lattice，包括值域V，和meet（ $\sqcap $ ）或者join（ ⊔ \sqcup ⊔ ）操作符
- F：是转换函数集（每个BB的转换函数可能不同）从V到V（从一个值域解到另一个解）
举例：将CFG和lattice联系起来：
6. 单调性和不动点理论
本节主要从理论方面解决问题：算法能保证会停止或者到达一个不动点吗，或者它保证一定有解吗？
eg：可达定义分析中，可以发现OUT不会缩水——这个就是单调性
-
单调性
定义：一个函数 f : L → L f:L \rightarrow L f:L→L（L是lattice）是单调的，满足 ∀ x , y ∈ L \forall x,y\in L ∀x,y∈L，都有 x ⊑ y ⇒ f ( x ) ⊑ f ( y ) x \sqsubseteq y \Rightarrow f(x) \sqsubseteq f(y) x⊑y⇒f(x)⊑f(y)
（通俗讲，就是x是y的偏序，那么f(x)是f(y)的偏序（用词可能不是很妥当））
-
不动点理论
给定一个完全lattice ( L , ⊑ ) (L,\sqsubseteq) (L,⊑)，如果 f : L → L f: L \rightarrow L f:L→L是单调的，并且 L L L有限
那么我们能得到最小不动点，通过迭代： f ( ⊥ ) , f ( f ( ⊥ ) ) , . . . , f k ( ⊥ ) f(\bot),f(f(\bot)),...,f^k(\bot) f(⊥),f(f(⊥)),...,fk(⊥)直到找到最小的一个不动点
同理 我们能得到最大不动点，通过迭代： f ( ⊤ ) , f ( f ( ⊤ ) ) , . . . , f k ( ⊤ ) f(\top),f(f(\top)),...,f^k(\top) f(⊤),f(f(⊤)),...,fk(⊤)直到找到最大的一个不动点‘
-
由此，我们进行证明：
-
不动点的存在性
（1）根据定义 ⊥ \bot ⊥（就是完全lattice L L L上最小的值）和 f : L → L f:L \rightarrow L f:L→L那么 f ( ⊥ ) f(\bot) f(⊥)仍为L上的值，则有 ⊥ ⊑ f ( ⊥ ) \bot \sqsubseteq f(\bot) ⊥⊑f(⊥)
（2）由于 f f f是满足单调性的，那么有 f ( ⊥ ) ⊑ f ( f ( ⊥ ) ) = f 2 ( ⊥ ) f(\bot) \sqsubseteq f(f(\bot))=f^2(\bot) f(⊥)⊑f(f(⊥))=f2(⊥)
（3）相同的，不断应用如上规律得到： ⊥ ⊑ f ( ⊥ ) ⊑ f 2 ( ⊥ ) ⊑ . . . ⊑ f i ( ⊥ ) \bot \sqsubseteq f(\bot)\sqsubseteq f^2(\bot)\sqsubseteq...\sqsubseteq f^i(\bot) ⊥⊑f(⊥)⊑f2(⊥)⊑...⊑fi(⊥)
（4）由于， L L L是有限的，那么一定存在一点为不动点 f f i x = f k ( ⊥ ) = f k + 1 ( ⊥ ) f^{fix} = f^k(\bot) = f^{k+1}(\bot) ffix=fk(⊥)=fk+1(⊥)，则这点就是不动点
-
最小不动点证明
（1）假设我们存在另一个不动点 x x x，根据不动点原理，就有 x = f ( x ) x = f(x) x=f(x)
（2）根据 ⊥ \bot ⊥的定义，满足 ⊥ ⊑ x \bot \sqsubseteq x ⊥⊑x
（3）由于f是单调的，那么有 f ( ⊥ ) ⊑ f ( x ) f(\bot) \sqsubseteq f(x) f(⊥)⊑f(x)
（4）假设 f i ( ⊥ ) ⊑ f i ( x ) f^i(\bot)\sqsubseteq f^i(x) fi(⊥)⊑fi(x)满足，由于f是满足单调性的，就有 f i + 1 ( ⊥ ) ⊑ f i + 1 ( x ) f^{i+1}(\bot)\sqsubseteq f^{i+1}(x) fi+1(⊥)⊑fi+1(x)，对于任意的 i i i，有 f i ( ⊥ ) ⊑ f i ( x ) f^i(\bot) \sqsubseteq f^i(x) fi(⊥)⊑fi(x)
（5）那么有 f i ( ⊥ ) ⊑ f i ( x ) = x f^i(\bot)\sqsubseteq f^i(x)=x fi(⊥)⊑fi(x)=x，就是当从 ⊥ \bot ⊥和x出发都找到不动点后（找到不动点后不管怎么计算都不变了），那么就有： f f i x = f k ( ⊥ ) ⊑ x f^{fix} = f^k(\bot)\sqsubseteq x ffix=fk(⊥)⊑x
所以，该不动点一定是最小的
=>同样证明最大不动点也是类似步骤。
-
7. 迭代算法转换到不动点理论
由于我们已经证明了不动点理论：完全lattice且是单调的、有限的，那么存在不动点且从 ⊤ \top ⊤开始找得到最大不动点和从 ⊥ \bot ⊥开始找得到最小不动点；现在的问题是：如何关联迭代算法和不动点理论（那么就能证明算法解存在、且最优）
目的：如下的迭代算法是否可以等价于一个 完全lattice ( L , ⊑ ) (L,\sqsubseteq) (L,⊑)，并且是有限的，函数是单调的：
-
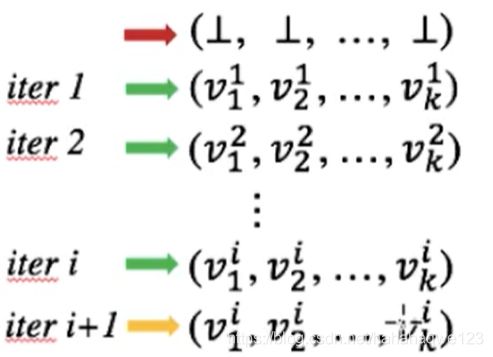
完全lattice证明：
通过第5节，可以发现，迭代算法的值域就可以用lattice来表达，那么每一个结点都对应一个lattice，那么每次迭代的k-元组（就是有k个BB ）——可以看成 lattice积——本身也是一个lattice，那么根据lattice积的性质：如果 L k L^k Lk中每一个lattice都是完全的，那么 L k L^k Lk也是完全
-
L是有限的证明：（值域是有界的）
很显然，在迭代算法中，值域是0/1，是有限的，那么lattice就是有限的，那么 L k L^k Lk也是有限的
-
f f f是单调的：
迭代算法中，函数 f f f就是：BB中的转换函数 f i : L → L f_i:L\rightarrow L fi:L→L + BB分支之间的控制流影响：只有merge操作会影响：有join/meet（分叉就是相同的一份复制粘贴传递到下一个BBs）
-
转换函数，本质上就是gen和kill，一旦BB确定，则gen、kill都是固定的，并且不会缩水的，一旦变成1了，就不会变回0（一旦变成1，就是survivor，说明不会被kill掉，那么就能一直存在）
——所以，显然转换函数是单调的
-
join/meet函数： L × L → L L \times L \rightarrow L L×L→L（这只是一个抽象的表示，实际中，可能有多个 L L L进行merge操作，但是可以看成两个两个进行merge操作，最后变成了一个 L L L）
先证明 ⊔ \sqcup ⊔：
证明：证明什么？—— ∀ x , y , z ∈ L \forall x,y,z\in L ∀x,y,z∈L，且有 x ⊑ y x\sqsubseteq y x⊑y需要证明 x ⊔ z ⊑ y ⊔ z x\sqcup z \sqsubseteq y\sqcup z x⊔z⊑y⊔z
(1)根据 ⊔ \sqcup ⊔ 的定义，有 y ⊑ y ⊔ z y \sqsubseteq y\sqcup z y⊑y⊔z
(2)根据传递性，有 x ⊑ y ⊔ z x \sqsubseteq y\sqcup z x⊑y⊔z
(3)所以， y ⊔ z y \sqcup z y⊔z是x的上界，也是z的上界（同1可以得出）
(4)而根据定义， x ⊔ z x\sqcup z x⊔z是x、z的最小上界，那么有 x ⊔ z ⊑ y ⊔ z x\sqcup z \sqsubseteq y\sqcup z x⊔z⊑y⊔z
所以命题得证，所以join/meet函数是单调的
——所以，merge操作是单调的
=> 所以，已经将两个前提满足了：单调性和有限性
=> 那么算法就能使用不动点理论了
=>算法一定能终止（到达一个不动点）；且算法得到的不动点是最小/最大不动点
（如下两个问题已经解决）
下面解决第三个问题：算法何时能到达不动点？-
先介绍一个lattice的性质：
lattice的高度：是lattice上从top到bottom之间最长的路径
eg：
-
可以求最坏的迭代次数
最坏的，每个BB的OUT/IN值只变化一个（0 -> 1类似），本质上就是lattice上只走一步（向上或者向下，只有一个方向）
并且，最坏是所有BBs中，只有一个BB的OUT/IN值发生变化，且变化一步
eg：算法中，有n个BB，且有k个变量，那么最多的迭代次数为 n × k n\times k n×k
-
8. 从lattice的角度看may/must分析
根据如下的图，逐步讲解整个过程：
需要记住的前提：
不论是may-analysis和must-analysis都是从不安全（unsafe result）到安全（safe result）
并且，may-analysis和must-analysis都是从准确（precise）到不准确（un-precise）
注意：现在是在对may/must analysis的算法整体流程分析，从lattice的角度。但是本身该算法是safe的——这是由safe-approximate来保证的，而不是通过lattice或者其他保证的。
-
may analysis
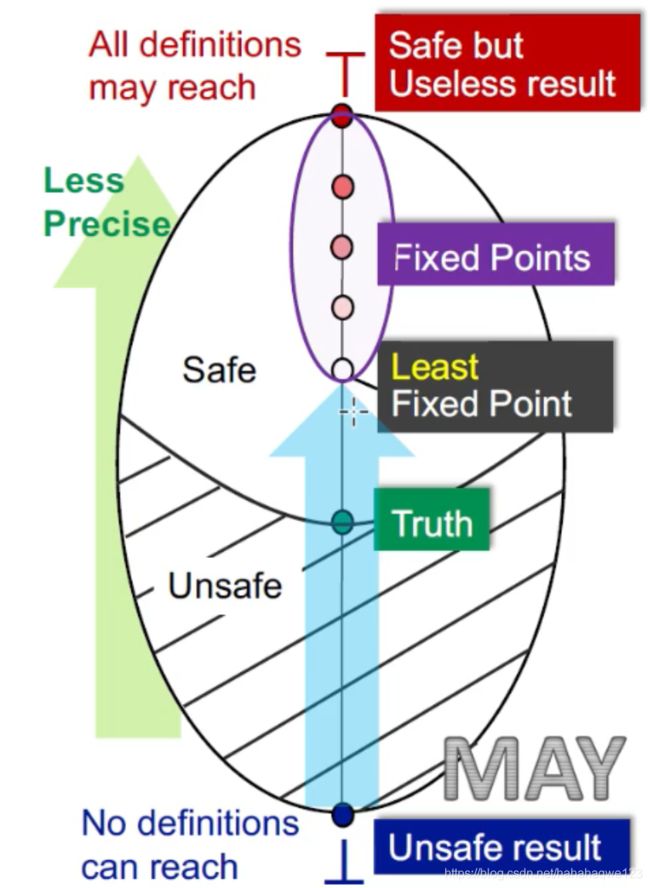
（BTW，这个图是真的赞）
may analysis以可达定义为例，-
从bottom开始，bottom代表的是所有定义都是可达的——这就是不安全的结果（ ∵ \because ∵验证本质上是一个查错的工具，现在的验证结果是没有错误，这就是不可靠的）
-
图中的no definitions can reach这个是根据可达性定义的应用来考虑的。可达性定义会应用在变量是否初始化中，它会在entry给每个变量一个假定义，这边的意思就是指所有的假定义都无法到达，那么就意味着程序中会将每个变量都初始化——那么就是该程序无未初始化错误——分析的结果是不安全的
-
最上面到top，top代表的是所有定义都是不可达的——从查错角度来讲，这句话是安全的，因为所有定义都有可能存在错误，但是这句话没有用——程序未验证前，就可以说这句话了——所以是safe but useless
-
图中的all definition may reach就是指，可达性定义应用中的那些个假定义，都是可达的，那么所有变量都是未初始化的——所有变量都存在未初始化的错误——分析的结果是安全的
-
中间的truth：
表明最准确的验证结果，假设{a,c}是truth，那么包括其以上的都是safe的，一下的都是unsafe，就是上图的阴影和非阴影。
-
并且都是从不安全到安全的过程——所以箭头从下向上
-
从bottom开始，得到的是最小不动点，就是离truth最近的，是最准确的。 向上还有多个不动点，但是准确度越来越不准（直到top就是最不准的）——may analysis得到的解是最小不动点，就是最优解
——所以，可达定义得到的是最准确的结果，虽然还是soundness的（过近似）
-
-
must analysis
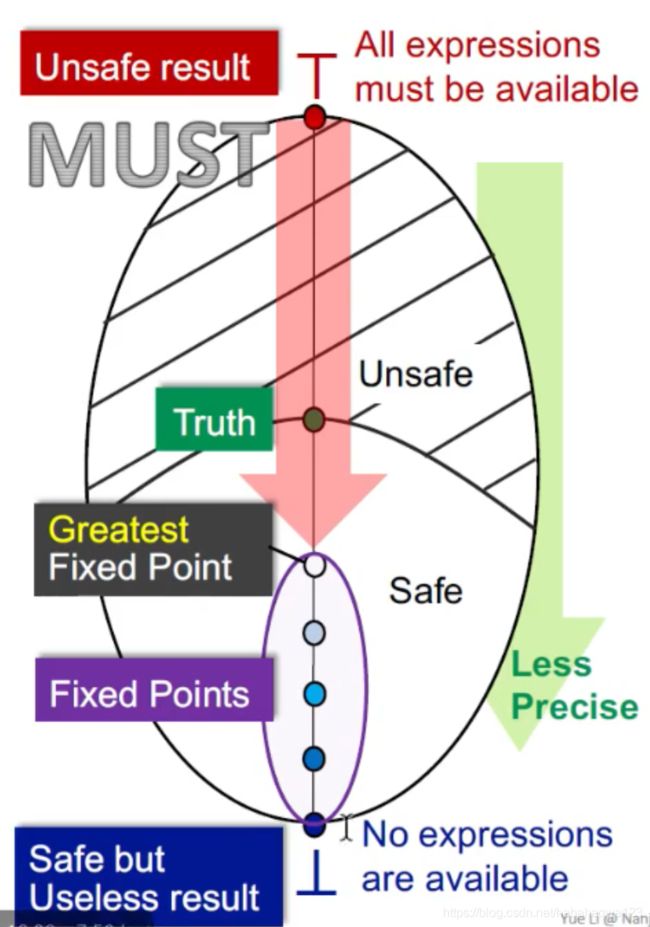
must analysis以available表达式为例。- 从top开始，代表所有表达式都是可用的——是最unsafe的——如果是利用在表达式计算优化中，那就是有很多已经被重新定义的表达是也被优化了（实际上不能被优化）——那么该优化就是错误的
- 到bottom，代表没有表达式是可用的——是安全的，但是是无用的
- 从top开始到bottom，就是不安全到安全的转变，存在一个truth，代表程序真实的结果；
- 分析从top到bottom，达到的就是最大不动点，离truth最近，那么该最大不动点得到的解就是最优的——must analysis得到的解是最大不动点，就是最优解
-
补充
分析为啥能达到最小/最大不动点：从步伐来解释：
将迭代算法转换到lattice上，考虑到了 f : L → L f:L\rightarrow L f:L→L，这个函数本质上就是算法中的转换函数和join/mmet操作构成的。
- 转换函数实际上是固定的，只要BB确定，那么其kill和gen是固定的，所以在lattice上走的步数是确定的
- join/mmet：lattice上就是求两个值的最小上界/最大下界，那么其走的步数也是最小的
=> 所以，函数在lattice上是走的最小步数，那么得到的不动点一定是离出发点最近的（从bottom出发就是最小不动点，从top出发就是最大不动点）
9. 结果和MOP
主要讲：MOP概念、MOP和迭代算法的精度比较
-
MOP：meet-over-all-paths solution（将所有路径都join/meet的方法），算是一个衡量精度的方法
ps：这边的meet是统称meet和join两种合并操作
路径P = 在cfg图上从entry到 s i s_i si的一条路径
路径P上的转移函数 F P F_P FP：是该路径上所有语句的转移函数的组合 f s 1 , f s 2 ， . . . f s i − 1 f_{s1},f_{s2}，...f_{si-1} fs1,fs2，...fsi−1，从而构成了 F P F_P FP 那么，MOP就是从entry到 s i s_i si所有路径的 F P F_P FP的meet操作：（那么就是求，这些值的最小上界/最大下界）
如下图就是MOP的式子：
但是，可能有些路径不会被执行，那么MOP实际上不是很准确（ ∵ \because ∵MOP是所有路径的meet） 如果路径中包含循环，那么就会陷入无终止的循环——unbounded——因为是静态分析，所以不知道循环结束的条件，所以，可能会不断执行下去
如果程序很大，程序可能会存在路径爆炸问题——not enumerable
=>所以，MOP可能不准确，实际操作性不高 => 是理论上的一个衡量方式
-
MOP和迭代算法的比较
对于如上的cfg：-
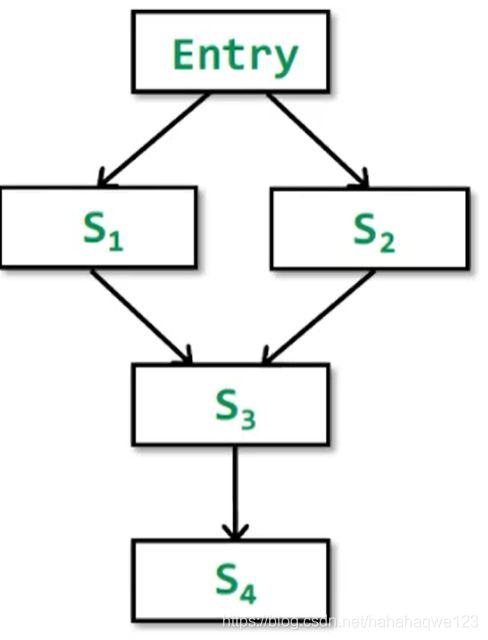
迭代算法得到IN[4]：
I N [ S 4 ] = f S 3 ( f S 1 ( O U T [ e n t r y ] ) ⊔ f S 2 ( O U T [ e n t r y ] ) ) IN[S_4] = f_{S_3}(f_{S_1}(OUT[entry])\sqcup f_{S_2}(OUT[entry])) IN[S4]=fS3(fS1(OUT[entry])⊔fS2(OUT[entry]))
到汇聚的时候，就meet
=> 将内部进行抽象：itter = F ( x ⊔ y ) F(x \sqcup y) F(x⊔y)
-
MOP得到IN[4]：
I N [ S 4 ] = f S 3 ( f S 1 ( O U T [ e n t r y ] ) ) ⊔ f S 3 ( f S 2 ( O U T [ e n t r y ] ) ) IN[S_4]=f_{S_3}(f_{S_1}(OUT[entry])) \sqcup f_{S_3}(f_{S2}(OUT[entry])) IN[S4]=fS3(fS1(OUT[entry]))⊔fS3(fS2(OUT[entry]))
就是每一条路径的meet
=> 将内部进行抽象：MOP = F ( x ) ⊔ F ( y ) F(x)\sqcup F(y) F(x)⊔F(y)
-
根据如上两者进行比较
1）根据最小上界lub的定义，可以得出： x ⊑ x ⊔ y x \sqsubseteq x\sqcup y x⊑x⊔y和 y ⊑ x ⊔ y y\sqsubseteq x\sqcup y y⊑x⊔y
2）由于转换函数是单调的，那么就有： F ( x ) ⊑ F ( x ⊔ y ) F(x)\sqsubseteq F(x\sqcup y) F(x)⊑F(x⊔y)和 F ( y ) ⊑ F ( x ⊔ y ) F(y) \sqsubseteq F(x \sqcup y) F(y)⊑F(x⊔y)，那么 F ( x ⊔ y ) F(x\sqcup y) F(x⊔y)就是 F ( x ) F(x) F(x)和 F ( y ) F(y) F(y)的上界
3）根据定义： F ( x ) ⊔ F ( y ) F(x)\sqcup F(y) F(x)⊔F(y)是 F ( x ) F(x) F(x)和 F ( y ) F(y) F(y)的最小上界
4）那么， F ( x ) ⊔ F ( y ) ⊑ F ( x ⊔ y ) F(x)\sqcup F(y)\sqsubseteq F(x\sqcup y) F(x)⊔F(y)⊑F(x⊔y)
∴ \therefore ∴MOP $\sqsubseteq $itter
那么就是MOP更加准确一点
-
如果F满足分配律，那么迭代算法和MOP精确度一样
F ( x ⊔ y ) = F ( x ) ⊔ F ( y ) F(x\sqcup y)=F(x)\sqcup F(y) F(x⊔y)=F(x)⊔F(y)
-
bit-vector（位向量）或者是gen/kill问题（对于join/meet是进行集合的交或并操作），那么就满足分配律
-
10. 数据流应用（课程作业相关）
常量传播（constant propagation）
-
定义：给定一个变量x在程序点p，判断是否在p时，x能确保有个常量的值
=> 根据定义，可以推断出：must analysis，是要考虑经过p点所有的路径上，x的值都必须是一样的，才算是保持常量
-
CFG图中每个结点的OUT必须是一对值**(x, v)**，x代表变量(名)，v代表x经过该点后所持有的值
-
数据流分析框架的确定 ( D , L , F ) (D,L,F) (D,L,F)
-
D：方向，数据流流向，它需要考虑在p点是否有常量的值，就需要看前面的，所以是forwards更直观
-
L：lattice
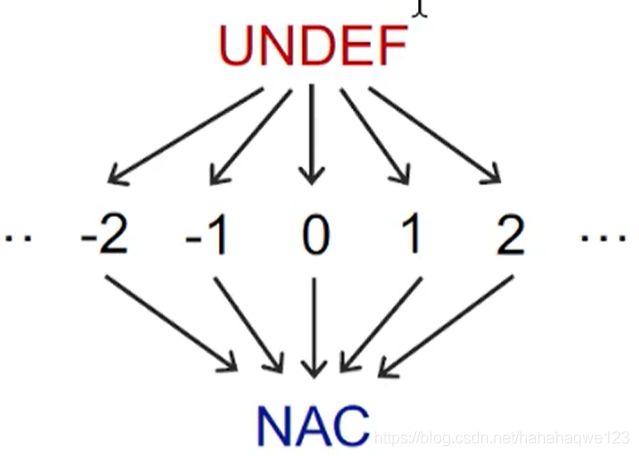
先确定lattice，可以看到变量的取值是所有实数都可以，并且是must-analysis从top开始（unsafe），所以top定义的是undefined（而不是，所有变量都是常数，因为从程序初始运行，就是所有变量都为定义）；bottom就是NAC，就是所有变量都是非常量再确定meet：因为是must-analysis，所以是 ⊔ \sqcup ⊔操作：
可能会出现如下情况：（所以不是常见的交和并）
-
F：转换函数定义如下：（和之前遇到的迭代算法类似）
含义：输入的减去BB中相关变量值已经不是f常量的部分；并上在BB中新被赋值的。将所有可能遇到的语句，进行分析：（如果，不是一个赋值语句就完全没影响）
-
-
性质：F不满足分配律
举例：
可以发现，不满足分配律，但是仍旧满足MOP比itter更精确
11. worklist 算法（是一种优化）——更常用
基本性质一样，只是一种优化
本质：就是将有变化的值挑出来，再去利用转换函数和控制流操作
终于把这两节看完，并整理完笔记了。今天刚得知老师不会再在b站上发布录屏视频了，只有直播。但是我正好也有一门验证课和直播冲突了，所以我有个大胆的想法。。。