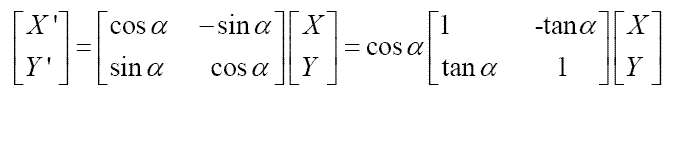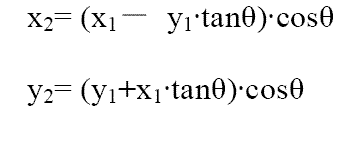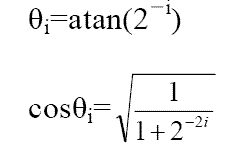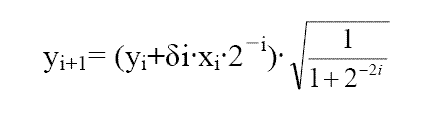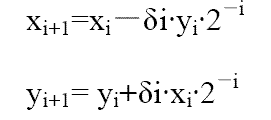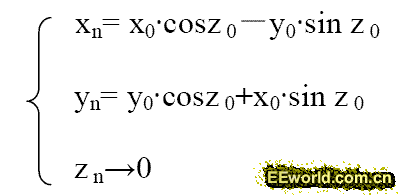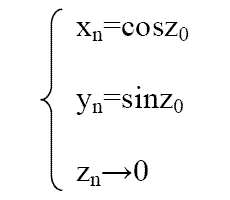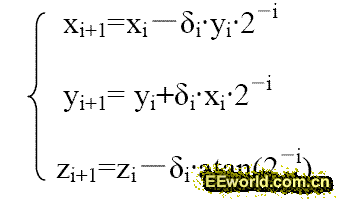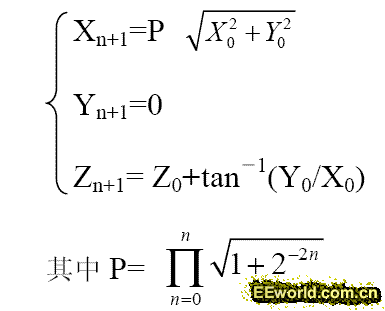CORDIC 算法理论与实践

CORDIC 算法可以在圆周，双曲坐标和线性下的用二维向量旋转后逐渐逼近的方式来计算出某个超越函数的近似值，虽然是近似值，但是如果迭代次数足够，仍然可以得到非常逼近准确结果的值。

下面分开讨论CORDIC 在圆周，双曲坐标和线性下的情况。
（1）圆周系统
先通过圆周系统来了解CORDIC 算法的基本思想。该算法的基本原理如图1

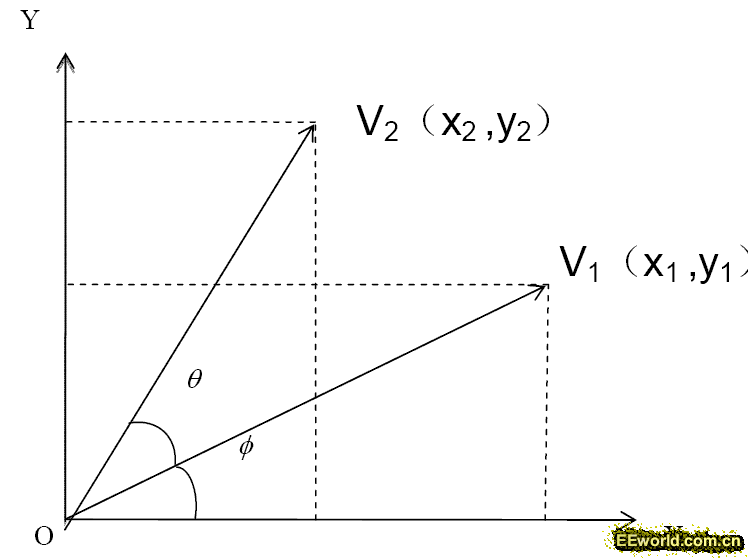
所示，现有向量V1，与X 轴夹角为Ф，逆时针旋转角度θ 后，得到新的向量
V2，

由上面的矩阵公司简化得到：

为了在硬件上实现方便，作如下约定：每一次旋转的角度θ正切值为2 的倍数，即

并且约定以δi 代表向量的旋转方向，+1 表示逆时针旋转，－1 表示顺时针旋转，故第i 步的旋转可用下式表示：

其中开根号的结果是模校正因子，对于字长一定的运算，它是一个常数，我们用K+1表示。以16bit 字长为例，

这样可将输入数据X，Y 校正后再参与运算，避免在运算中增加校正运算。运算迭代式可以简化成：

上式运算就只有加或减法和移位了。上面的公式n 次迭代可以得到：

假设给定X0=K+1;Y0=0， 则迭代结果：

所以，将所需产生的角度值作为z0 输入，迭代结果输出xn 和yn 就是需要的浮点超越函数值。采用的迭代方程组为：

CORDIC 算法在圆周系统中还可以用向量模式表达出来。向量模式将输入向量通过一个特定的角将Y 变为0。该模式下的CORDIC 公式类似于旋转模式，不同的是旋转的方向取决于Y 而不是Z 的符号。N 次迭代后CORDIC 公式变为：

从上面的推导可以看出，CORDIC 算法在圆周系统下的向量模式可以用来计算给定向量(X，Y)的长度和角。这显然就是从迪卡尔坐标到极坐标的转换。

下面给出一个CORDIC算法在圆周系统下的向量模式下获取角度的Verilog 程序：

/*==============================================================================*\
Filename : Cordic.v
Discription : 坐标旋转数字计算方法。通过该算法，对输入的向量坐标进行9次迭代
计算，得到该向量的模值和相角。

\*==============================================================================*/

module CORDIC
(
Clk_20m,
_Rst,
Cordic_start,
Ug_d,
Ug_q,
Ug,
Delta

);

input Clk_20m,
_Rst,
Cordic_start; //CORDIC变换启动标志

input[15:0] Ug_d, //输出电压的d轴分量
Ug_q; //输出电压的q轴分量
output[15:0] Ug; //输出电压向量的模值
output[13:0] Delta; //输出电压向量的相角

wire[31:0] Ug_tmp;
reg[3:0] Times; //迭代次数累加器
reg[15:0] Ug_d_tmp, //输出电压d轴分量的中间迭代结果
Ug_q_tmp; //输出电压q轴分量的中间迭代结果

reg[13:0] //Delta,
Delta_tmp; //相位角旋转累加寄存器


// assign Ug = ( Ug_d_tmp>>1 ) + ( Ug_d_tmp>>3 ) - ( Ug_d_tmp>>6 ) - ( Ug_d_tmp>>9 );

//对电压模值进行比例系数调整，得到实际模值的32倍
// assign Ug_tmp[31:0] = Ug_d_tmp[15:0] * 16'd48224;//d39797;
assign Ug_tmp[31:0] = Ug_d_tmp[15:0] * 16'd45208;
assign Ug[15:0] = Ug_tmp[31:16];

//输出电压向量的相角即为CORDIC算法输出的旋转角
assign Delta = Delta_tmp;
/*
always @( posedge Clk_20m or negedge _Rst )
begin
if ( !_Rst )
Delta <= 14'h0;
else if ( Delta_tmp <= 14'h6 )
Delta <= Delta_tmp;
else if ( Delta_tmp <= 14'h1fff )
Delta <= 14'h6;
else if ( Delta_tmp <= 14'h3ffa )
Delta <= 14'h3ffa;
else
Delta <= Delta_tmp;

else
Delta <= 14'h6;

end

*/

always @( posedge Clk_20m or negedge _Rst )
begin
if ( !_Rst )
begin
Times[3:0] <= 4'hf;
Ug_d_tmp[15:0] <= 16'h0;
Ug_q_tmp[15:0] <= 16'h0;
Delta_tmp[13:0] <= 14'h0;
end
else if ( Cordic_start ) //启动CORDIC变换
begin
Times[3:0] <= 4'h0;
Ug_d_tmp <= Ug_d;
Ug_q_tmp <= Ug_q;
Delta_tmp <= 14'h0;
end
else if ( Times <= 4'd9 ) //开始迭代计算
begin
Times[3:0] <= Times[3:0] + 4'h1; //迭代次数加1
case ( Times )
4'h0:

//Ug_q_tmp[15] 符号位
if ( Ug_q_tmp[15] ) //旋转的目标是使Ug_q_tmp趋近于0,
//根据对Ug_q_tmp符号的判断，决定正向旋转还是反向旋转
begin
Ug_d_tmp <= Ug_d_tmp - Ug_q_tmp; //重新计算新的d轴分量
Ug_q_tmp <= Ug_q_tmp + Ug_d_tmp; //重新计算新的q轴分量
Delta_tmp <= Delta_tmp - 14'hB40; //对相位角进行累加计算
end
else
begin
Ug_d_tmp <= Ug_d_tmp + Ug_q_tmp;
Ug_q_tmp <= Ug_q_tmp - Ug_d_tmp;
Delta_tmp <= Delta_tmp + 14'hB40; //(2880/64)=45
end
4'h1:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { Ug_q_tmp[15], Ug_q_tmp[15:1] };
Ug_q_tmp <= Ug_q_tmp + { Ug_d_tmp[15], Ug_d_tmp[15:1] };
Delta_tmp <= Delta_tmp - 14'h6A4; // (1700/64)=26.5625
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { Ug_q_tmp[15], Ug_q_tmp[15:1] };
Ug_q_tmp <= Ug_q_tmp - { Ug_d_tmp[15], Ug_d_tmp[15:1] };
Delta_tmp <= Delta_tmp + 14'h6A4; //
end
4'h2:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {2{Ug_q_tmp[15]}}, Ug_q_tmp[15:2] };
Ug_q_tmp <= Ug_q_tmp + { {2{Ug_d_tmp[15]}}, Ug_d_tmp[15:2] };
Delta_tmp <= Delta_tmp - 14'h382; // (382/64=14.03125)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {2{Ug_q_tmp[15]}}, Ug_q_tmp[15:2] };
Ug_q_tmp <= Ug_q_tmp - { {2{Ug_d_tmp[15]}}, Ug_d_tmp[15:2] };
Delta_tmp <= Delta_tmp + 14'h382;
end
4'h3:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {3{Ug_q_tmp[15]}}, Ug_q_tmp[15:3] };
Ug_q_tmp <= Ug_q_tmp + { {3{Ug_d_tmp[15]}}, Ug_d_tmp[15:3] };
Delta_tmp <= Delta_tmp - 14'h1c8; // (382/64=14.03125)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {3{Ug_q_tmp[15]}}, Ug_q_tmp[15:3] };
Ug_q_tmp <= Ug_q_tmp - { {3{Ug_d_tmp[15]}}, Ug_d_tmp[15:3] };
Delta_tmp <= Delta_tmp + 14'h1c8; // (456/64=7.125)
end
4'h4:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {4{Ug_q_tmp[15]}}, Ug_q_tmp[15:4] };
Ug_q_tmp <= Ug_q_tmp + { {4{Ug_d_tmp[15]}}, Ug_d_tmp[15:4] };
Delta_tmp <= Delta_tmp - 14'hE5; //(229/64=3.578125)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {4{Ug_q_tmp[15]}}, Ug_q_tmp[15:4] };
Ug_q_tmp <= Ug_q_tmp - { {4{Ug_d_tmp[15]}}, Ug_d_tmp[15:4] };
Delta_tmp <= Delta_tmp + 14'hE5;
end
4'h5:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {5{Ug_q_tmp[15]}}, Ug_q_tmp[15:5] };
Ug_q_tmp <= Ug_q_tmp + { {5{Ug_d_tmp[15]}}, Ug_d_tmp[15:5] };
Delta_tmp <= Delta_tmp - 14'h72; //(114/64=1.78125)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {5{Ug_q_tmp[15]}}, Ug_q_tmp[15:5] };
Ug_q_tmp <= Ug_q_tmp - { {5{Ug_d_tmp[15]}}, Ug_d_tmp[15:5] };
Delta_tmp <= Delta_tmp + 14'h72;
end
4'h6:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {6{Ug_q_tmp[15]}}, Ug_q_tmp[15:6] };
Ug_q_tmp <= Ug_q_tmp + { {6{Ug_d_tmp[15]}}, Ug_d_tmp[15:6] };
Delta_tmp <= Delta_tmp - 14'h39;//(57/64=0.890625)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {6{Ug_q_tmp[15]}}, Ug_q_tmp[15:6] };
Ug_q_tmp <= Ug_q_tmp - { {6{Ug_d_tmp[15]}}, Ug_d_tmp[15:6] };
Delta_tmp <= Delta_tmp + 14'h39;
end
4'h7:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {7{Ug_q_tmp[15]}}, Ug_q_tmp[15:7] };
Ug_q_tmp <= Ug_q_tmp + { {7{Ug_d_tmp[15]}}, Ug_d_tmp[15:7] };
Delta_tmp <= Delta_tmp - 14'h1C;//(28/64=0.4375)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {7{Ug_q_tmp[15]}}, Ug_q_tmp[15:7] };
Ug_q_tmp <= Ug_q_tmp - { {7{Ug_d_tmp[15]}}, Ug_d_tmp[15:7] };
Delta_tmp <= Delta_tmp + 14'h1C;
end
4'h8:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {8{Ug_q_tmp[15]}}, Ug_q_tmp[15:8] };
Ug_q_tmp <= Ug_q_tmp + { {8{Ug_d_tmp[15]}}, Ug_d_tmp[15:8] };
Delta_tmp <= Delta_tmp - 14'hE;//(14/64=0.21875)
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {8{Ug_q_tmp[15]}}, Ug_q_tmp[15:8] };
Ug_q_tmp <= Ug_q_tmp - { {8{Ug_d_tmp[15]}}, Ug_d_tmp[15:8] };
Delta_tmp <= Delta_tmp + 14'hE;
end
4'h9:
if ( Ug_q_tmp[15] )
begin
Ug_d_tmp <= Ug_d_tmp - { {9{Ug_q_tmp[15]}}, Ug_q_tmp[15:9] };
Ug_q_tmp <= Ug_q_tmp + { {9{Ug_d_tmp[15]}}, Ug_d_tmp[15:9] };
Delta_tmp <= Delta_tmp - 14'h7;
end
else
begin
Ug_d_tmp <= Ug_d_tmp + { {9{Ug_q_tmp[15]}}, Ug_q_tmp[15:9] };
Ug_q_tmp <= Ug_q_tmp - { {9{Ug_d_tmp[15]}}, Ug_d_tmp[15:9] };
Delta_tmp <= Delta_tmp + 14'h7; //(7/64=0.109375)
end
default: //缺省情况下所有寄存器清零
begin
Ug_d_tmp <= 16'h0;
Ug_q_tmp <= 16'h0;
Delta_tmp <= 14'h0;
end
// ;
endcase
end
else
Times[3:0] <= 4'hf; //迭代计算完毕，结束CORDIC算法，迭代次数置复位值


end

endmodule