剑指Offer and Leetcode刷题总结之思想1：动态规划

目录

剑指10-II：剑指10-II：青蛙跳台阶问题/Leetcode70

Leetcode70：爬楼梯

剑指12：矩阵中的路径

剑指14-I/剑指14-II：剪绳子I/II（题解参考）/Leetcode343||动态规划||找规律

剑指19：正则表达式匹配

剑指42：连续子数组的最大和/Leetcode53：最大子序和

剑指46：把数字翻译成字符串

剑指47：礼物的最大价值

剑指60：n个骰子的点数

剑指63：股票的最大利润/Leetcode12

Leetcode05：最长回文子序列 ||Leetcode647：回文子串（输出数量）

Leetcode42：接雨水

Leetcode62：不同路径

Leetcode64：最小路径和

Leetcode72：编辑距离（题解参考）

Leetcode84：柱状图中最大的矩形

Leetcode85：最大矩形

Leetcode198：打家窃舍

Leetcode279：完全平方数

Leetcode300：最长上升子序列

Leetcode322：零钱兑换（题解参考）

Leetcode1143：最长公共子序列

---

剑指10-II：剑指10-II：青蛙跳台阶问题/Leetcode70

==> 跟下一题Leetcode70：爬楼梯思路完全一致；

==> 斐波那契函数，用lambda实现；

fib = lambda n : n if n <= 2 else fib(n-1) + fib(n-2

class Solution10(object):
    """
    方法1：
    基本思路：dp[n] = dp[n-1] + dp[n-2]
    时间复杂度 and 空间复杂度：O(n)
    """
    def numWays(self, n):
        if n == 0: return 1
        if n == 1: return 1
        dp = [0 for _ in range(n+1)]
        dp[0], dp[1] = 1, 1
        for i in range(2, n+1):
            dp[i] = dp[i-1] + dp[i-2]
        print(dp)
        return dp[n] % 1000000007
    
    """
    优化版：空间复杂度O(1)
    """
    def numWays(self, n):
        if n == 0: return 1
        if n == 1: return 1
        a = 1
        b = 1
        for i in range(2, n+1):
            tmp = a + b
            a = b
            b = tmp
        return b % 1000000007

Leetcode70：爬楼梯

题目：假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。

class Solution70():
    """
    方法1：动态规划:
    到第n阶的方法数等于到第n-1阶和第n-2阶的方法数之和
    """
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        f1 = 1 # 到第一阶的方法数为1
        f2 = 2 # 到第二阶的方法是为2
        if n ==1: return f1
        if n ==2: return f2
        for i in range(3, n+1):
            ans = f1 + f2
            f1 = f2
            f2 = ans
        return ans

剑指12：矩阵中的路径

剑指14-I/剑指14-II：剪绳子I/II（题解参考）/Leetcode343||动态规划||找规律

题目：给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例：输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1

基本思路：1. 找规律，尽可能切分为长度为3的小段，时间复杂度为O(1)；2. dp[i] = max(dp[i], k * (i-k), k * dp[i-k]) 切下来k之后，要比较(i-k)和dp[i-k]的大小，时间复杂度为O(n*n)

class Solution14(object):
    """
    方法1：找规律
    基本思路：均可以分解为2和3为最小的子绳子段
    """
    def cuttingRope(self, n):
        if n == 1: return 1
        if n == 2: return 1
        if n == 3: return 2
        a = n % 3
        b = n // 3
        if a == 0: return pow(3, b)
        if a == 1: return pow(3, b-1) * 4
        return pow(3, b) * 2
    """
    方法2：动态规划
    """
    def cuttingRope(self, n):
        dp = [0 for _ in range(n+1)]
        dp[1] = 1
        dp[2] = 1
        for i in range(3, n+1):
            for k in range(2, i):
                # 1.dp[i]:不剪绳子；2.剪成两段k * (i - k); 3.剪一段i-k下来，另外dp[k]再分配；
                dp[i] = max(dp[i], k * (i-k), (i-k) * dp[k]) # 切下来k之后，要比较(i-k)和dp[i-k]的大小
        return dp[n]

剑指19：正则表达式匹配

剑指42：连续子数组的最大和/Leetcode53：最大子序和

==>Leetcode152：乘积最大子数组

题目：给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例：输入: [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。

基本思路：同时维护一个imax以及一个imin，在nums[i]<0的时候交换imax和imin；

class Solution42(object):
    """
    首道动态规划题，略难理解
    时间复杂度为O(n)
    空间复杂度为O(1)
    """
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if len(nums) <= 1:
            return nums[0]
        for i in range(1, len(nums)):
            nums[i] = nums[i] + max(0, nums[i-1])
        return max(nums)
    
    """
    另外还有分治递归（时间复杂O(nlogn);空间复杂O(logn)）以及暴力法(时间复杂O(n*n);空间复杂(1))，后期完善
    """
##############乘积最大子数组##############
class Solution(object):
    def maxProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        size = len(nums)
        if size == 1: return nums[0]
        imax = imin = 1
        ans = 0
        for i in range(size):
            if nums[i] < 0:
                tmp = imin
                imin = imax
                imax = tmp
            imax = max(nums[i], nums[i] * imax)
            imin = min(nums[i], nums[i] * imin)
            ans = max(ans, imax)
        return ans

剑指46：把数字翻译成字符串

题目：给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

示例：输入: 12258 输出: 5 解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

基本思路：见代码

class Solution:
    def translateNum(self, num: int) -> int:
        str_num = str(num)
        if not str_num: return 0
        size = len(str_num)
        if size == 1: return 1
        dp = [1 for _ in range(len(str_num)+1)]
        for i in range(2, len(str_num)+1):
            if str_num[i-2] == '1' or (str_num[i-2] == '2' and str_num[i-1] <= '5'):
                dp[i] = dp[i-1] + dp[i-2]
            else:
                dp[i] = dp[i-1]
        return dp[-1]

剑指47：礼物的最大价值

题目：在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

基本思路：动态规划

class Solution47(object):
    """
    方法1：动态规划
    val[i][j] = max(val[i-1][j], val[i][j-1]) + grid[i][j]
    时间复杂度：O(m*n)
    空间复杂度：O(m*n) 空间复杂度后续可以优化，当前element只与当前row以及last row有关，所以其实可以只维护2rows，空间复杂度为O(n)// 继续改进，可以!!!原地修改!!!数组，空间复杂度就变为O(1)了
    """
    def maxValue(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        if not grid: return 0
        row = len(grid)
        col = len(grid[0])
        val = [[0 for _ in range(col)] for _ in range(row)]
        for i in range(row):
            for j in range(col):
                if i == 0 and j == 0:
                    val[i][j] = grid[i][j]
                elif i == 0:
                    val[i][j] = max(0, val[i][j-1]) + grid[i][j]
                elif j == 0:
                    val[i][j] = max(val[i-1][j], 0) + grid[i][j]
                else:
                    val[i][j] = max(val[i-1][j], val[i][j-1]) + grid[i][j]
        return val[row-1][col-1]
    
    """
    方法2：动态规划(空间复杂度优化+外圈元素先处理掉)
    val[i][j] = max(val[i-1][j], val[i][j-1]) + grid[i][j]
    时间复杂度：O(m*n)
    空间复杂度：O(1)
    """
    def maxValue_02(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        if not grid: return 0
        row = len(grid)
        col = len(grid[0])
        for j in range(1, col): grid[0][j] = grid[0][j - 1] + grid[0][j]
        for i in range(1, row): grid[i][0] = grid[i - 1][0] + grid[i][0]
        for i in range(1, row):
            for j in range(1, col):
                grid[i][j] = max(grid[i-1][j], grid[i][j-1]) + grid[i][j]
        return grid[-1][-1]

剑指60：n个骰子的点数

题目：把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

基本思路：dp[n][s] = dp[n-1][s-1] + dp[n-1][s-2] + dp[n-1][s-3] + dp[n-1][s-4] + dp[n-1][s-5] + dp[n-1][s-6]

class Solution:
    def twoSum(self, n: int) -> List[float]:
        # dp[n][s] = dp[n-1][s-1] + dp[n-1][s-2] + dp[n-1][s-3] + dp[n-1][s-4] + dp[n-1][s-5] + dp[n-1][s-6]
        dp = [[0 for _ in range(n * 6 + 1)] for _ in range(n + 1)]
        for i in range(1, 7):
            dp[1][i] = 1
        for i in range(2, n + 1):
            for j in range(i, i * 6 + 1):
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j-2] + dp[i-1][j-3] + dp[i-1][j-4] + dp[i-1][j-5] + dp[i-1][j-6]
        ans = []
        for m in range(n, n * 6 + 1):
            ans.append(dp[n][m] * 1.0 / (6**n)) # 总共有6**n种可能情况
        return ans

剑指63：股票的最大利润/Leetcode12

基本思路：仅买卖一次；维护最小值以及最大利润即可；

==>Leetcode122：买卖股票最佳时机II

基本思路：等价于每一天都买卖（涨则买卖，跌则不买卖）--画折线图理解；

==>Leetcode123：买卖股票的最佳时机 III

基本思路：三维状态方程；

"""仅买卖一次"""
class Solution63(object):
    """
    方法1：记录最小股价与最大利润
    """
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        if not prices:return 0
        min_pr = prices[0]
        max_pf = 0
        for i in range(1, len(prices)):
            if prices[i] < min_pr:
                min_pr = prices[i]
            if prices[i] - min_pr > max_pf:
                max_pf = prices[i] - min_pr
        return max_pf
    
    """
    方法1：简化版
    """
    def maxProfit(self, prices):
        if len(prices) <= 1: return 0
        mi, pr = prices[0], 0
        for e in prices[1: ]:
            mi = min(e, mi)
            pr = max(pr, e-mi)
        return pr
    
    """
    方法2：动态规划，原理相同，还是存储最低价格与最大利润，仅仅用单变量存储最大利润即可
    """
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        if not prices: return 0
        max_pf = 0
        for i in range(1, len(prices)):
            max_pf = max(max_pf, prices[i] - prices[i - 1])
            prices[i] = min(price[i - 1], prices[i])
        return max_pf  

"""可买卖多次"""
class Solution(object):
    """
    方法1：等价于每一天都买卖（涨则买卖，跌则不买卖）
    """
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        ans = 0
        if not prices: return 0
        for i in range(1, len(prices)):
            tmp = prices[i] - prices[i-1] 
            if tmp > 0:
                ans += tmp
        return ans

"""可买卖2次"""
class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        # dp[天数][当前是否持股][卖出的次数]
        if not prices: return 0
        size = len(prices)
        dp = [[[0, 0, 0], [0, 0, 0]] for _ in range(size)]
        # 从未进行过买卖
        for i in range(size):
            dp[i][0][0] = 0
        dp[0][1][0] = -prices[0] # 第一天买入
        for i in range (2):
            for j in range(1, 3):
                dp[0][i][j] =  float('-inf') # 第一天不可能有卖出
        for i in range(1, size):
            dp[i][0][1] = max(dp[i-1][1][0]+prices[i], dp[i-1][0][1]) # 未持股，卖出过1次，可能是今天卖的，也可能是之前卖的；
            dp[i][0][2] = max(dp[i-1][1][1]+prices[i], dp[i-1][0][2]) # 未持股，卖出过2次，可能是今天卖的，也可能是之前卖的；
            dp[i][1][0] = max(dp[i-1][0][0]-prices[i], dp[i-1][1][0]) # 持股，未卖出过，可能是今天买的，也可能是之前买的；
            dp[i][1][1] = max(dp[i-1][0][1]-prices[i], dp[i-1][1][1]) # 持股，卖出过1次，可能是今天买的，也可能是之前买的；
            dp[i][1][2] = float('-inf')
        return max(dp[size-1][0][1], dp[size-1][0][2], 0)

Leetcode05：最长回文子序列 ||Leetcode647：回文子串（输出数量）

题目2：给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。

示例：输入: "abc" ；输出: 3；解释: 三个回文子串: "a", "b", "c".

基本思路：与最长回文子序列逻辑相同，这个只是统计数量；

class Solution05():
    """
    没有特别的思路，直接暴力解法时间复杂度是O(n*n*判断回文序列的时间复杂度)
    这个解法超出了时间限制。。。
    """
    def isPalindrome(self, s):
        if len(s) <= 1: return True
        return s[0] == s[-1] and self.isPalindrome(s[1:-1]) 
    
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if len(s) <= 1: return s
        ma = 0
        for i in range(len(s)):
            for j in range(i+1, len(s)+1):
                if self.isPalindrome(s[i: j]):
                    if j - i + 1 > ma:
                        ma = j - i + 1
                        ans = s[i: j]
                else:
                    j += 1
            i += 1
        return ans
        
    """
    方法2：
    动态规划
    时间复杂度：N*N
    空间复杂度：N*N
    """
    def isPalindrome_02(self, s):
        if len(s) < 2:
            return s
        start = 0
        max_len = 1
        dp = [[False for _ in range(len(s))] for _ in range(len(s))]
        for i in range(len(s)):
            dp[i][i] = True
#         print(dp)
        for j in range(1, len(s)):
            for i in range(0, j):
                if s[i] == s[j]:
                    if j - i > 2:
                        dp[i][j] = dp[i+1][j-1]
                    else:
                        dp[i][j] = True
#                 else: # 不操作，初始值就是Fasle
#                     dp[i][j]= False
                if dp[i][j] and j - i + 1 > max_len:
                    max_len = j - i + 1
                    start = i
#         print('max_len = %d and start = %d' % (max_len, start))
        return s[start: start+max_len]

class Solution647(object):
    def countSubstrings(self, s):
        """
        :type s: str
        :rtype: int
        """
        size = len(s)
        if size < 2: return size
        dp = [[False for _ in range(size)] for _ in range(size)]
        for i in range(size):
            dp[i][i] = True
        ans = 0
        for j in range(1, size):
            for i in range(j):
                if s[i] == s[j]:
                    if j - i <= 2:
                        dp[i][j] = True
                    else:
                        dp[i][j] = dp[i+1][j-1] 
                if dp[i][j]:
                    ans += 1
        return ans + size

Leetcode42：接雨水

题目：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

基本思路：

1. left_max[i]表示左边柱子最高的高度left_max=max(left_max[i-1], height[i-1])

2. right_max[i]表示右边柱子最高的高度right_max=max(right_max[i+1], height[i+1])

3. 求出left_max和right_max较低的值，比height[i]高，则可以积水，否则不能积水

面试题：给定一个数组，存的是容器的高度，index值是高度间的差，求怎么样选取两个高度，使得构成的容器体积最大

class Solution(object):
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        if not height: return 0
        ans = 0
        size = len(height)
        left_max = [0 for _ in range(size)]
        right_max = [0 for _ in range(size)]
        left_max[0] = height[0]
        right_max[-1] = height[-1]
        for i in range(1, size):        # left_max[i]表示左边柱子最高的高度left_max=max(left_max[i-1], height[i-1])
            left_max[i] = max(left_max[i-1], height[i-1])
        for i in range(size-2, -1, -1): # right_max[i]表示右边柱子最高的高度right_max=max(right_max[i+1], height[i+1])
            right_max[i] = max(right_max[i+1], height[i+1])
        for i in range(1, size-1):      # 求出left_max和right_max较低的值，比height[i]高，则可以积水，否则不能积水
            low = min(left_max[i], right_max[i])
            if low > height[i]:
                ans += low - height[i]
        return ans

Leetcode62：不同路径

题目：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？

基本思路：dp[i][j] = dp[i-1][j] + dp[i][j-1]

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        dp = [[0 for _ in range(m)] for _ in range(n)]
        dp[0][0] = 1
        for j in range(1, m):
            dp[0][j] = 1
        for i in range(1, n):
            dp[i][0] = 1
        for i in range(1, n):
            for j in range(1, m):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[n-1][m-1]

Leetcode64：最小路径和

题目：给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。说明：每次只能向下或者向右移动一步。

示例: 输入: [   [1,3,1], [1,5,1], [4,2,1] ]；输出: 7；解释: 因为路径 1→3→1→1→1 的总和最小。

基本思路：dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])

class Solution64():
    def minPathSum(self, grid):
        """
        """
        row, col = len(grid), len(grid[0])
        dp = [[0 for _ in range(col)] for _ in range(row)]
        for i in range(row):
            for j in range(col):
                if i == 0 and j != 0:
                    dp[i][j] = grid[i][j] + dp[i][j-1]
                elif i != 0 and j == 0:
                    dp[i][j] = grid[i][j] + dp[i-1][j]
                elif i == 0 and j == 0:
                    dp[i][j] = grid[i][j]
                else:
                    dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1])
        return dp[row][col]

Leetcode72：编辑距离（题解参考）

题目：给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。你可以对一个单词进行如下三种操作：插入一个字符；删除一个字符；替换一个字符

示例：输入：word1 = "horse", word2 = "ros"；输出：3；解释：horse -> rorse (将 'h' 替换为 'r')；rorse -> rose (删除 'r')；rose -> ros (删除 'e')；

基本思路：

对“dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。”的补充理解：

以 word1 为 "horse"，word2 为 "ros"，且 dp[5][3] 为例，即要将 word1的前 5 个字符转换为 word2的前 3 个字符，也就是将 horse 转换为 ros，因此有：

(1) dp[i-1][j-1]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 2 个字符 ro，然后将第五个字符 word1[4]（因为下标基数以 0 开始） 由 e 替换为 s（即替换为 word2 的第三个字符，word2[2]）

(2) dp[i][j-1]，即先将 word1 的前 5 个字符 horse 转换为 word2 的前 2 个字符 ro，然后在末尾补充一个 s，即插入操作

(3) dp[i-1][j]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 3 个字符 ros，然后删除 word1 的第 5 个字符

class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        size1, size2 = len(word1), len(word2)
        dp = [[0 for _ in range(size2 + 1)] for _ in range(size1 + 1)]
        for j in range(1, size2 + 1): # 第一行
            dp[0][j] = dp[0][j-1] + 1
        for i in range(1, size1 + 1): # 第一列
            dp[i][0] = dp[i-1][0] + 1

        for i in range(1, size1 + 1):
            for j in range(1, size2 + 1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
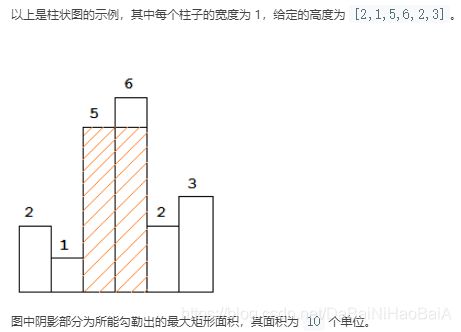
        return dp[-1][-1]

Leetcode84：柱状图中最大的矩形

题目：给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

基本思路：

Leetcode85：最大矩形

题目：给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

基本思路：

Leetcode198：打家窃舍

题目：你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例：输入：[1,2,3,1]；输出：4；解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。

基本思路：f(n) = max(f(n-2)+nums[n], f(n-1)) 

class Solution198():
    """
    标准动态规划题目：f(n) = max(f(n-2)+nums[n], f(n-1)) 
    """
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums: return 0
        if len(nums) <= 2: return max(nums)
        f1 = nums[0]
        f2 = max(f1, nums[1])
        for i in range(2, len(nums)):
            ans = max(f1 + nums[i], f2)
            f1 = f2
            f2 = ans
        return ans

Leetcode279：完全平方数

题目：给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例：输入: n = 12 输出: 3 解释: 12 = 4 + 4 + 4.

基本思路：dp[5] = min(dp[5], dp[5 - 2*2] + 1), +1 means j*j提供的一种组合；

时间复杂度：O(n*sqrt(n)) || 空间复杂度：O(n)

class Solution(object):
    def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        dp = [i for i in range(0, n+1)] # 最坏情况：1 = 1; 2 = 1 + 1; 3 = 1 + 1 + 1
        for i in range(1, n+1):
            for j in range(1, int(sqrt(i))+1):
                dp[i] = min(dp[i], dp[i - j*j] + 1) # dp[5] = min(dp[5], dp[5 - 2*2] + 1), +1 means j*j提供的一种组合
        return dp[-1]

Leetcode300：最长上升子序列

class Solution300(object):
    """
    方法一：
    时间复杂度O(n)
    空间复杂度O(n) -- 需要存放状态list
    """
    def lengthOfLIS(self, nums):
        size = len(nums)
        if size < 2: return size
        dp = [1 for _ in range(size)]
        for i in range(1, size):
            for j in range(0, i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)
    
    def lengthOfLIS(self, nums):
        size = len(nums)
        if size < 2: return size
        tail = [nums[0]]
        for i in range(1, size):
            if nums[i] > tail[-1]:
                tail.append(nums[i])
            else:
                left, right = 0, len(tail) - 1
                while(left < right):
                    mid = (right + left) >> 1
                    if tail[mid] < nums[i]:
                        left = mid + 1
                    else:
                        right = mid 
                tail[left] = nums[i]
        return len(tail)

Leetcode322：零钱兑换（题解参考）

题目：给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例：输入: coins = [1, 2, 5], amount = 11 输出: 3 解释: 11 = 5 + 5 + 1

基本思路：动态转移方程 -- dp[i] = min(dp[i], dp[i - coins[j]] + 1)

时间复杂度：O(amount * len(coins)) and 空间复杂度：O(amount)

class Solution(object):
    def coinChange(self, coins, amount):
        """
        :type coins: List[int]
        :type amount: int
        :rtype: int
        """
        dp = [amount + 1 for _ in range(amount + 1)]
        dp[0] = 0
        for i in range(1, amount + 1):
            for j in range(len(coins)):
                if i >= coins[j]: # 只有在当前amount >= coins面值的时候才继续往下进行
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1)
        return -1 if dp[amount] > amount else dp[amount]

Leetcode1143：最长公共子序列

基本思路：状态方程：dp[i][j] = max(dp[i-1][j], dp[i][j-1])

时间复杂度：O(m*n) and 空间复杂度：O(m*n)

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        """
        :type text1: str
        :type text2: str
        :rtype: int
        """
        m, n = len(text1), len(text2)
        if m == 0 or n == 0: return 0  # bad case
        # 这里要在外圈留一圈0，防止以下的[i-1]或者[j-1]取到0以下，取到[0]时为0
        dp = [[0 for _ in range(m+1)] for _ in range(n+1)] 
        for i in range(1, n+1): 
            for j in range(1, m+1):
                if text1[j-1] == text2[i-1]: # 难理解：当i=3 and j=3时，text1和test2的长度为3，index为0..2，所以取到最后一个数字为i-1 or j-1 
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[n][m]